NCERT Solutions for Class 9 Science Chapter 8 Motion, contains solutions to various questions in Exercises for Chapter 8. Motion Class 9 NCERT Solutions have been explained in a simple and easy to understand manner. NCERT Solutions for Class 9 help to check the concept you have learned from detailed classroom sessions and the application of your knowledge.
| Category | NCERT Solutions for Class 9 |
| Subject | Science |
| Chapter | Chapter 8 – Motion |
Download NCERT Solutions for Class 9 Science Chapter 8 – Motion
NCERT Solutions for Class 9 Science Chapter 8 Motion Question Answers
1. An object has moved through a distance. Can it have zero displacement? If yes, support your answer with an example.
Answer.
Yes, an object can have zero displacement even when it has moved through a distance. This happens when final position coincides with the initial position. For example, in going from home to school and coming back to home, some distance is travelled but displacement is zero.
2. A farmer moves around the boundary of a square field of side 10m in 40s. What will be the magnitude of displacement of the farmer at the end of 2 minutes 20 seconds?
Answer.
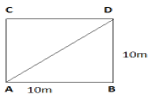
ABCD is a square filed of side 10m.
Time for one round = 40s
Total time = 2min 20 sec = 140 seconds
Number of rounds completed = 140/40 = 3.5
If the farmer starts from A, he will complete 3 rounds at A. In last 0.5 round starting from A, he will finish at C. Displacement = AC
AC = √AB² + BC²
= √10² + 10²
= 10√2 m
3. What is true for displacement?
a) It cannot be zero.
b) Its magnitude is greater than the distance travelled by the object.
Answer.
a) Displacement can be zero. This statement is not true.
b) Magnitude of displacement is never greater than the distance travelled by the object. This statement is not true.
Class 9 Science Chapter 8 Motion Question Answers
Intex Questions Page No. 10
1. Distinguish between speed and velocity.
Answer.
Velocity is speed in a particular direction. Speed is scalar, but velocity is vector.
2. Under what conditions the magnitude of average velocity of an object is equal to its average speed.
Answer.
When a body moves in a straight line, the magnitude of average velocity of the object is equal to its average speed.
3. What does the odometer of an automobile measure?
Answer.
Odometer of an automobile measures the distance travelled by the vehicle.
4. What does the path of an object look like when it is in uniform motion?
Answer.
In uniform motion, the path of an object can be straight line, curved line, zig-zag or even circle. It can have any shape. As in uniform motion, the speed of the object is constant. The direction of motion may change.
5. During an experiment the signal of spaceship reached the ground station in five minutes. What was the distance of the spaceship from the ground station? The signal travels with the speed of light, i.e. 3 x 108 m/s.
Answer.
Given, speed of light = 3 x 108 m/s
Time taken by the signal in reaching the earth = 5 min = 5 x 60 = 300 sec
Distance of the spaceship from the ground station
= speed x time
= 3 x 108 x 300 = 9 x 1010m
NCERT Solutions for Class 9 Science Chapter Motion
Intext Questions – Page No. 103
1. When will you say a body is in
i. Uniform acceleration
ii. Non-uniform acceleration
Answer.
i. A body is said to be in uniform acceleration when its velocity changes by an equal amount in equal intervals of time
ii. A body is said to be in non-uniform motion when its velocity changes by unequal amount in equal time intervals.
2. A bus decrease sits speed from 80km/h to 60km/hr in 5s. Find the acceleration of the bus.
Answer.
We know, 1km/hr = 5/18 m/s
Given, initial speed of the bus, u =80km/h =80 x 5/18 = 22.22m/s
Final speed of the bus, v =60km/hr =60 x 5/18 = 16.67m/s
Time taken to decrease the speed, t = 5s
Acceleration of the bus, a = (v – u) / t
a = 16.67 – 22.22 / 5 = -1.11m/s2
Negative side indicates that the velocity of the bus is decreasing i.e. the bus retards.
3. A train starting from a railway station and moving with uniform acceleration attains a speed of 40km/h in 10 min. Find its acceleration.
Answer.
Initial velocity of the train, u = 0
Final velocity of the train, v = 40km/h = 40 x 5/18 = 11.11m/s
Time taken = 10 min = 10 x 60 = 600s
Acceleration, a = (v – u) / t = (11.11 – 0) / 600 = 1.855 x 10-2 m/s2
Hence, acceleration of the train is 1.855 x 10-2 m/s2
Class 9 Science Chapter 8 NCERT Solutions
Page No. 107
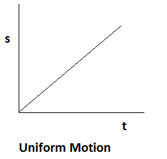
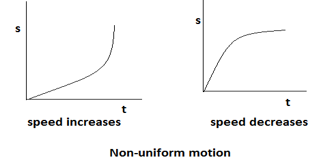
1. What is the nature of distance-time graph for uniform and non-uniform motion of an object
Answer.
The distance time graph for uniform motion of an object is a straight line.
Distance-time graph for non-uniform motion is a curved line.
2. What can you say about the motion of an object whose distance-time graph is a straight line parallel to the time axis?
Answer.
When the distance time graph is a straight line parallel to the time axis, it indicates that the object is at rest since the position of the object is not changing with time.
3. What can you say about the motion of an object, if the speed-time graph is a straight line parallel to time axis?
Answer.
Speed-time graph is a straight line parallel to time axis indicates that the speed of the object is not changing with time hence speed of the object is constant.
4. What is the quantity which is measured by the area occupied below the velocity-time graph?
Answer.
The area occupied below the velocity-time graph gives the displacement of the object.
Class 9 Science Chapter 8 Motion NCERT Solutions
Intext Questions – Page No. 109
1. A bus starting from rest moves with a uniform acceleration of 0.1m/s2 for 2min. Find:
i. The speed acquired
ii. The distance travelled
Answer.
Given, acceleration, a = 0.1m/s2
Time, t = 2min = 120s
Object starts from rest so, u = 0
i. From first equation of motion, v = u + at
v = 0 + 0.1(120) = 12m/s
Hence, speed acquired by the object will be 12m/s.
ii. From 2nd equation of motion, s = ut + ½ at2
s = 0 + ½(0.1)(120)2 = 720m
Hence, distance travelled by the object is 720m
Chapter 8 Motion Class 9 Questions Answers
Page No. 110
1. A train is travelling at speed of 90km/h. Brakes are applied, so as to produce a uniform acceleration of -0.5m/s2. Find how far the train will go before it comes to rest.
Answer.
Given, initial speed, u = 90km/h
= (90 x 5/18) = 25m/s
Acceleration, a = -0.5m/s2
Train is brought to rest, so final speed, v = 0
From 3rd equation of motion, v2 = u2 + 2as
0 = (25)2 + 2(-0.5)s
s= 625m
Thus, the train will cover a distance of 625m before it is brought to rest.
2. A trolley while going down an inclined plane has an acceleration of 2cm/s2. What will be its velocity 3s after the start?
Answer.
Given, initial velocity, u= 0
Acceleration, a= 2cm/s2 = 0.02m/s2
Time taken = 3s
From 1st equation of motion, v = u + at
V = 0 + (0.02)(3) = 0.06m/s
Hence, the velocity of the trolley after 3s of start is 0.06m/s.
3. A racing car has a uniform acceleration of 4m/s2. What distance will it cover in 10s after the start?
Answer.
Given, acceleration, a =4m/s2
Time taken, t = 10s
Initial velocity, u= 0
From 2nd equation of motion, s = ut + ½ at2
s = 0 + ½ x 4 x (10)2 = 200m
Hence, distance covered by racing car in 10s is 200m.
4. A stone is thrown in vertically upward direction with a velocity of 5m/s. If the acceleration of the stone during its motion is 10m/s2 in the downward direction, then what will be the height attained by the stone and what time will it take to reach there?
Answer.
Given, initial velocity, u = 5m/s
Acceleration, a = -10m/s2
Final velocity, v = 0
From 3rd equation of motion, v2 – u2 = 2as
0 – 52 = 2 x -10x s
s = 25/20 = 1.25m
Therefore, 1.25m will be the height attained by the stone.
From 1st equation of motion, v = u + at
0 = 5 + (-10) t
t = 5/10 = 0.5s
Motion Class 9 Questions Answers Science Chapter 8
Page No. 112 and 113
1. An athlete completes one round of a circular track of diameter 200m in 40s.What will be the distance covered and displacement at the end of 2min 20s.
Answer.
Given, diameter of the track= 200m
So, radius, r = 100m
Time, t = 2min 40sec = 140s
In 40s, athlete covers 1 round
So, in 140s, athlete covers = 140/40 = 3.5 rounds
Hence, distance covered by the athlete = 3.5 x 2πr = 3.5 x 2 x 22/7 x 100 = 2200m
Displacement is the shortest path covered = 2r = 2 x 100 = 200m
2. Joseph jogs from one end A to other end B of a straight 300m road in 2min 30s and then turns around and jogs 100m back to point C in another 1 min. What are Joseph’s average speeds and velocities in jogging
i. From A to B
ii. From A to C?
Answer.
i. From A to B, Joseph covers distance= 300m
Time taken = 2min 30s = 150s
Hence, average speed= total distance/ total time
= 300/150 = 2m/s
Average velocity = total displacement / total time
= 300/150 = 2m/s.
In this case, both distance and displacement covered is same.
ii. From A to C, Distance travelled by Joseph = 400m
Time taken = 150+60 = 210s
So, average speed = total distance/ total time
= 400/210 = 1.9m/s
Displacement = 200m
Time = 150 + 60 = 210s
Average velocity = total displacement / total time
= 200/210 = 0.952m/s
3. Abdul, while driving to school, computes the average speed for his trip to be 20km/h. On his return trip along the same route, there is less traffic and the average speed is 30km/h. What is the average speed for Abdul’s trip?
Answer.
Let the distance covered by Abdul while driving to school = s
If t1 is the time taken to reach the school, then
t1 = distance / average speed = x / 20
If t2 is the time taken to return back, then
t2 = distance / average speed = x / 30
Total time = t1 + t2
= (x / 20 + x / 30) = x/12
Total distance = x + x = 2x
Average speed = 2x / (x/12) = 24km/h
4. A motorboat starting from rest on a lake accelerates in a straight line at a constant rate of 3.0m/s2 for 8.0 s. How far does the boat travel during this time?
Answer.
Initial velocity, u = 0
Acceleration, a = 3m/s2
Time taken = 8.0s
From 2nd equation of motion, s = ut + ½ at2
s = 0 + ½ 3 x (8)2 = 96m
Hence, boat travels a distance of 96m.
5. A driver of a car travelling at 52km/h applies breaks and accelerates uniformly in the opposite direction. The car stops in 5s. Another driver going at 35km/h in another car applies his breaks slowly and stops in 10s. On the same graph paper plot speed versus time graph of two cars. Which of the two cars travelled farther, after the brakes were applied?
Answer.
Here, initial speed of Car I, u = 52km/h = 52 x 5/18 = 14.4m/s
Final speed, v = 0; time taken, t = 5s
Acceleration, a = (v – u) / t
= (0 – 14.4) / 5 = -2.88m/s2
For Car II, u = 34km/h = 34 x 5/18 = 9.4m/s
Acceleration = v – u / t
= (0 – 9.4) / 10 = -0.94m/s2
Negative sign shows retardation.
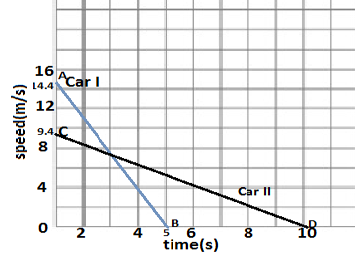
As distance travelled = Area enclosed between the speed time graph and time axis, thus Distance travelled by Car I= Area of ΔOAB
= ½ X 5 X 14.4 = 36m
Distance travelled by the Car II before it stops = Area of
= ½ X 9.4 x 10 = 47m
Therefore, Car II has travelled farther distance after the brakes were applied.
6. Fig 1.57 shows the distance-time graph of three objects, A, B and C. Study the graph and answer the following questions:
a) Which of the three is travelling the fastest?
b) Are all three ever on the same point on the road?
c) How far has C travelled when B passes A?
d) How far has B travelled by the time it passes C?
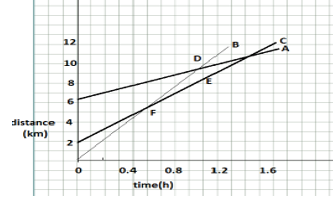
Answer.
a) As slope of distance-time graph represents speed, B has the maximum speed and will thus move the fastest.
b) For meeting at any point on the road, respective distance and time values must be same for all the three objects at that point. As this condition is not present in given graph, three objects will never meet on the road.
c) B passes A at D. At this time, C is at E, which corresponds to 7km. Hence, C is at 7km from the origin.
d) B crosses C at F at a distance of 4.5km from the origin.
7. A ball is gently dropped from a height of 20m. If its velocity increases uniformly at the rate of 10m/s2, with what velocity will it strike the ground?
Answer.
Given, height = Distance = 20m
Acceleration, a = 10m/s2
Final velocity, v =?
s = ut + ½ at2
20 = 0 + ½ 10(t)2
t = 2s
v = u + at
v = 0 + 10×2 = 20m
8. The speed time graph of a car is shown.
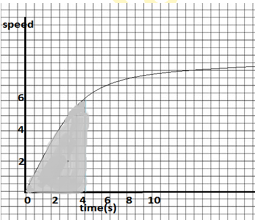
a) Find how far does the car travel in first 4 seconds.Shade the area on the graph that represents the distance travelled by the car during this period.
b) Which part of the graph represents uniform motion of the car?
Answer.
a) To calculate the distance travelled by the car, we need to find the number of squares in the shaded portion. It comes out to be 320.5 squares,
As one square on X-axis represents t = 1/6s and each square on Y-axis represents v= 1/3m/s. Thus, area of each square = v x t = 1/3 x 1/6 = 1/ 18m2
Total area of 320.5 squares = 320.5 x 1/18 = 17.80m
b) In uniform motion, the speed of the body is constant. In graph, t = 6s to t = 10s represents uniform motion of the car.
9. State which of the following situations are possible and give an example of each of these.
a) A body with a constant acceleration but zero velocity.
b) An object moving in a certain direction with an acceleration in the perpendicular direction.
Answer.
a) A body with constant acceleration and zero velocity is possible, For example, when a body is just released, its initial velocity, u = 0 but acceleration= g= 10m/s2
b) It is possible. For example, when a body is moving uniformly in a circle, acceleration is acting towards the centre of the circle while the velocity at any instant is tangent to the circle. Thus, the acceleration is directed in perpendicular direction.
10. An artificial satellite is moving in a circular orbit of radius 42250km. Calculate the speed if it takes 24 hours to revolve around the earth.
Answer.
Given, r = 42250km;
t = 24h;
From v = 2
v = (2 x 22/7 x 42250) / 24 = 1.1 x 104 km/h
Hence, speed of the satellite is 1.1 x 104 km/h
Topics Covered in Motion Class 9 Science
- Types of Motion
- Average Speed and Average Velocity
- Rate of Change of Velocity
- Graphical Representation of Motion
- Graphical Representation of Equation of Motion
- Uniform Circular Motion
NCERT Solutions for Class 9 Science