Linear Equations Worksheet for Class 6 contains 9 MCQ questions. Answers to Linear Equations Worksheet for Class 6 are available after clicking on the answer. Maths Worksheets for Class 6 help to check the concept you have learnt from detailed classroom sessions and application of your knowledge.
| Category | Maths Worksheets for Class 6 |
| Subject | Maths |
| Chapter | Linear Equations |
1. If a number triple itself and the result is increased by 5 we get 35. Find the number?
a) 8
b) 12
c) 10
Answer
Answer: c) 10
Explanation
Let the required number be x
If the Number is triple itself, we get 3 × x
We know that,
3 × x + 5 = 35
Transposing + 5 to -5 (Addition Changes to Subtraction)
3x = 35 – 5
3x = 30
x =30/3
x = 10
The required number is x = 10
2. If a number double itself and the result is increased by 4 we get 34. Find the number?
a) 14
b) 15
c) 13
Answer
Answer: b) 15
Explanation
Let the required number be x
If the Number is double itself, we get 2 × x
We know that,
2 × x + 4 = 34
Transposing + 4 to -4 (Addition Changes to Subtraction)
2x = 34 – 4
2x = 30
x = 30/2
x = 15
The required number is x = 15
3. Find the value of “a” if,
2a + 9 = 57 – 6a
a) 7
b) 6
c) 8
Answer
Answer: b) 6
Given Equation:
2a + 9 = 57 – 6a
In the given expression, write variables on one side and Exponents on other side
Therefore,
2a + 9 = 57 – 6a
Transposing + 9 to -9
2a + 6a = 57 – 9
Take “a” as common and add the variables
( 2 + 6 )a = 48
8a = 48
a = 48/8
Divide Numerator and Denominator with their HCF i.e, 8
![]()
a = 6/1
a = 6
Hence, the value of “a” is 6
4. 6 times a number is 42
a) 6 + a = 42
b) 6a = 42
c) 6 + 42 = a
Answer
Answer: b) 6a = 42
Explanation
Suppose, the required number is ‘ a ‘
So, 6 times the number will be 6a
Therefore, 6a = 42
Hence, the Required Equation is
6a = 42
5. Verify by substitution, whether one of the root of the equation 5a – 7 = 23 is true, when a = 6
a) True
b) False
Answer
Answer: a) True
Explanation
Given Equation :
5a – 7 = 23
Now, replace the value of a = 6 in the given equation
On substituion, the given equation becomes 5 x 6 – 7 = 23
According to BODMAS Rule, we will do multiplication first, i.e 5 x 6 = 30
Therefore, the equation would now be 30 – 7 = 23 or 23 = 23
LHS = RHS = 23
Hence, a = 6 verified.
6. Find the Value of “a” if, (4a+8)/6 = 4
a) 4
b) 6
c) 5
Answer
Answer: a) 4
Explanation
(4a+8)/6 = 4
On Cross Multiplying,
4a + 8 = 4 x 6
4a + 8 = 24
Transposing + 8 to -8 (Addition Changes to Subtraction)
4a = 24 – 8
4a = 16
On Cross Multiplying
a = 16/4
a = 16/4 = 4/1 = 4
Value of a = 4
7. If a bag contains 25 paisa and 50 paisa coins whose total values is Rs 25 and if the number of 25 paisa coins is two times that of 50 paisa coins, find the number of each type of coins ?
a) 15, 60
b) 35, 40
c) 25, 50
Answer
Answer: c) 25, 50
Explanation
Let number of the 50 paisa coins be x
As 25 paisa coins are 2 times of 50 paisa coins
Therefore, the number of 25 paisa coins will be ( 2 × x )
Now, we are given that
50 × x + 25 × ( 2 × x ) = 2500
Both the expressions have same Variable so we can add them,
or 50 × x + 50 × x = 2500
Take x as common
( 50 + 50 )x = 2500
100x = 2500
x = 2500/100
x = 25
Therefore the number of 50 paisa coins is 25
Number of 25 paisa coins = 2 × x
Number of 25 paisa coins = 2 × 25
Number of 25 paisa coins = 50
8. Solve the given equation for the value of a?
4a/5 = 24
a) 32
b) 30
c) 27
Answer
Answer: b) 30
Explanation
Given Equation:
4a/5 = 24
On Cross Multiplication,
4a = 24 x 5
4a = 120
Therefore,
a = 120/4
Dividing both the Numerator and Denominator by their HCF i.e, 4
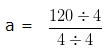
= 30/1 = 30
So, the value of ‘a’ = 30
9. If Samiksha is 12 years older than Kanchan and the sum of their age is 36 years, what are their present ages ?
a) 12 , 24
b) 11 , 25
c) 13 , 23
Answer
Answer: a) 12 , 24
Explanation
Let the present age of Kanchan be 1a
Since Samiksha is 12 years older than Kanchan
Present age of Samiksha will be ( 1a + 12 ) years
Given,
Sum of their ages = 36
i.e,
1a + ( 1a + 12 ) = 36
Take “a” as common
( 1 + 1 )a + 12 = 36
2a + 12 = 36
Transposing + 12 to -12 (Addition Changes to Subtraction)
2a = 36 – 12
2a = 24
or in other words
a = 24/2
a = 12
Present age of Kanchan = 12 Years
Present age of Samiksha = (1 x a + 12) years
= (1 x 12 + 12) years
= 24 years
Maths Worksheets for Class 6
- Area and Perimeter Worksheets Grade 6
- Factors and Multiples Class 6 Worksheets
- Fractions Class 6 Worksheet
- Ratio and Proportion Class 6 Worksheet
- Integers Worksheet for Class 6
- Whole numbers Class 6 Worksheet
- Decimals Class 6 Worksheet
- Triangles Worksheet for Class 6
- 3D Shapes Faces Edges Vertices Worksheets
- Linear Equations Worksheet for Class 6
- Algebraic Expressions for Class 6 Worksheets
- Basic Geometrical Ideas
2 thoughts on “Linear Equations Worksheet for Class 6”
It was helpful. Keep on posting!
The sums are easy try to make them hard.