Algebraic Expressions for Class 6 Worksheets contains 8 MCQ questions. Answers to Algebraic Expressions for Class 6 Worksheets are available after clicking on the answer. Maths Worksheets for Class 6 help to check the concept you have learnt from detailed classroom sessions and application of your knowledge.
| Category | Maths Worksheets for Class 6 |
| Subject | Maths |
| Chapter | Algebraic Expressions |
1. Identify the numerical coefficient of terms (other than constant) in the given expression.
4x+3y+7
a) 4, 3, 7
b) 4, 3
Answer
Answer: b) 4, 3
Explanation
4x+3y+7
In the given expression, various terms (other than the constant 7 ) are as under : –
4x – Numerical Coefficient of 4x is 4.
3y – Numerical Coefficient of 3y is 3.
2. State whether a given pair of terms is of Like terms or Unlike terms?
7x, 7y
a) Like terms
b) Unlike terms
Answer
Answer: b) Unlike terms
Explanation
When two terms have same variables and same power of each variable then those terms are called like terms otherwise unlike terms. The constant can be different. All constants are like terms.
The given terms are Unlike Terms, since both the terms have different variables , i.e, the first term 7x has a variable x and the second term 7y has a variable y.
3. State whether a given pair of terms is of Like terms or Unlike terms?
4xy, 7xy
a) Like terms
b) Unlike terms
Answer
Answer: a) Like terms
Explanation
When two terms have same variables and same power of each variable then those terms are called like terms otherwise unlike terms. The constant can be different. All constants are like terms.
Both the given terms are Like Terms, since both the terms have same variables , i.e, “xy”
4. Write the following in exponential form:
b x b x b x b x b x 19 times
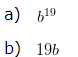
Answer
Answer: a) ![]()
Explanation
Given
b x b x b x b x b x 19 times
= b x 19 times
= ![]()
Algebraic Expressions for Class 6 Worksheets
5. If a = 7 and b = 3 then, Find the value of a + 6b
a) 25
b) 39
Answer
Answer: a) 25
Explanation
Given:
a = 7
b = 3
Given expression
a + 6b
Now we will replace a = 7 and b = 3
= 7 + 6 x 3
According to BODMAS rule we will do multiplication first
= 7 + 18
then, Addition
= 25
6. Check whether the given equation is true or false on substituting the value of variables?
5a – 2b = 3c , when a = 3 , b = 4 and c = 2
a) True
b) False
Answer
Answer: b) False
Explanation
LHS: 5a – 2b
Substitute the value, a = 3 and b = 4 in the given expression
We get,
( 5 x a ) – ( 2 x b )
= ( 5 x 3 ) – ( 2 x 4 )
According to BODMAS rule we will do multiplication first
= 15 – 8
then, Addition
= 7
On Solving RHS,
RHS = 3c
Substituting the value , c = 2
RHS = 3 x 2
RHS = 6
Hence, LHS ≠ RHS
So, the above expression is FALSE
7. Subtract 5a from 13a.
a) 6a
b) 4a
c) 8a
Answer
Answer: c) 8a
Explanation
Given Expression :
13a and 5a
Both the expression have same Variable so we can substract them,
Here,
Constants = 13 and 5
Variable = a
Therefore,
13a – 5a
Taking ” a ” as common we get
= ( 13 – 5 )a
= 8a
8. Add the terms 7a and 4a
a) 11a
b) 11a²
Answer
Answer: a) 11a
Explanation
Since both the expression have same Variable, we can add them
Given expression are 7a and 4a
Here 7 and 4 are constants
and ” a ” is variable
7 x a + 4 x a
Taking “a” as common
( 7 + 4 )a
11a
Maths Worksheets for Class 6
- Area and Perimeter Worksheets Grade 6
- Factors and Multiples Class 6 Worksheets
- Fractions Class 6 Worksheet
- Ratio and Proportion Class 6 Worksheet
- Integers Worksheet for Class 6
- Whole numbers Class 6 Worksheet
- Decimals Class 6 Worksheet
- Triangles Worksheet for Class 6
- 3D Shapes Faces Edges Vertices Worksheets
- Linear Equations Worksheet for Class 6
- Algebraic Expressions for Class 6 Worksheets
- Basic Geometrical Ideas