Arinjay Academy » Maths » Fractions Worksheets Grade 4

Fractions Worksheets Grade 4

Download Fractions Worksheets Grade 4

Fractions Worksheets Grade 4

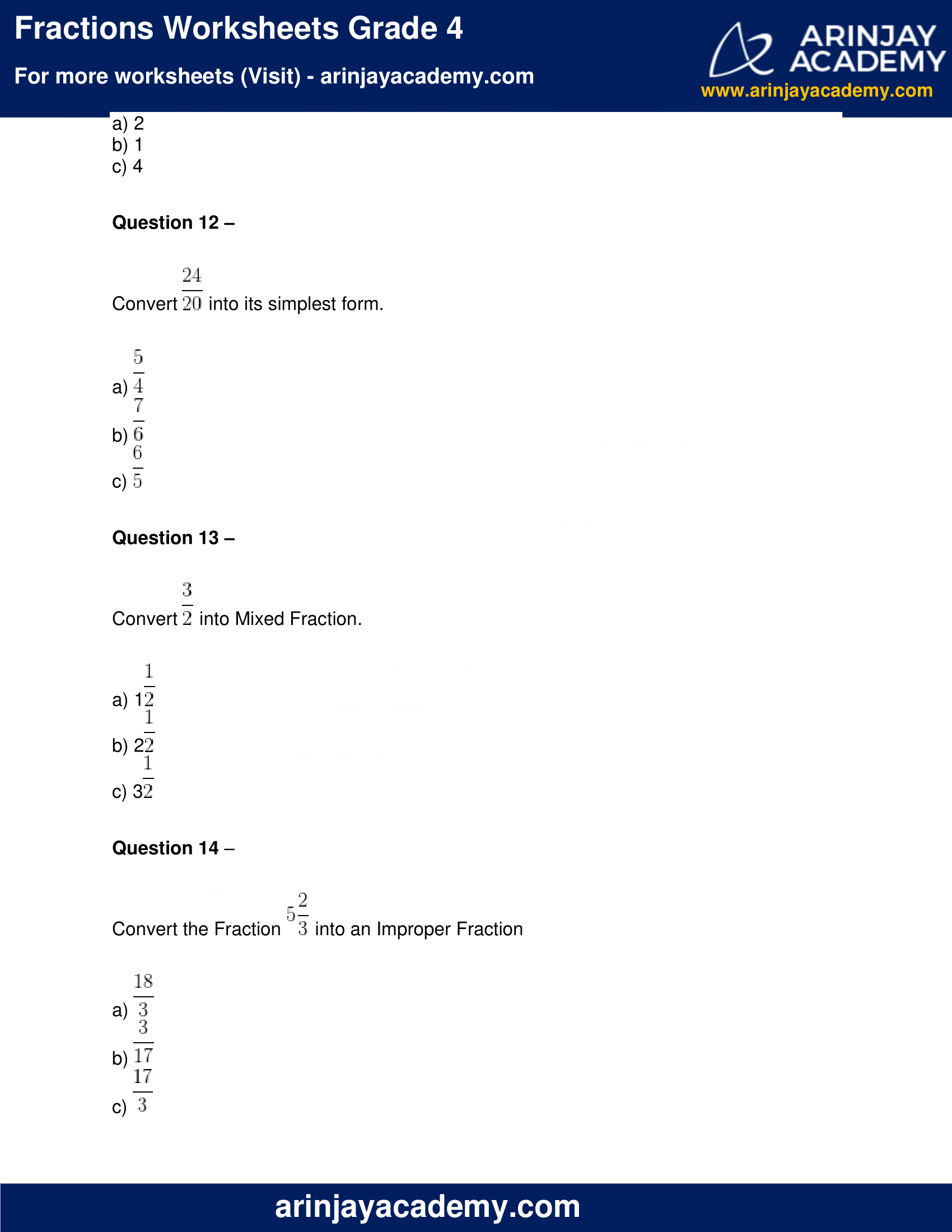
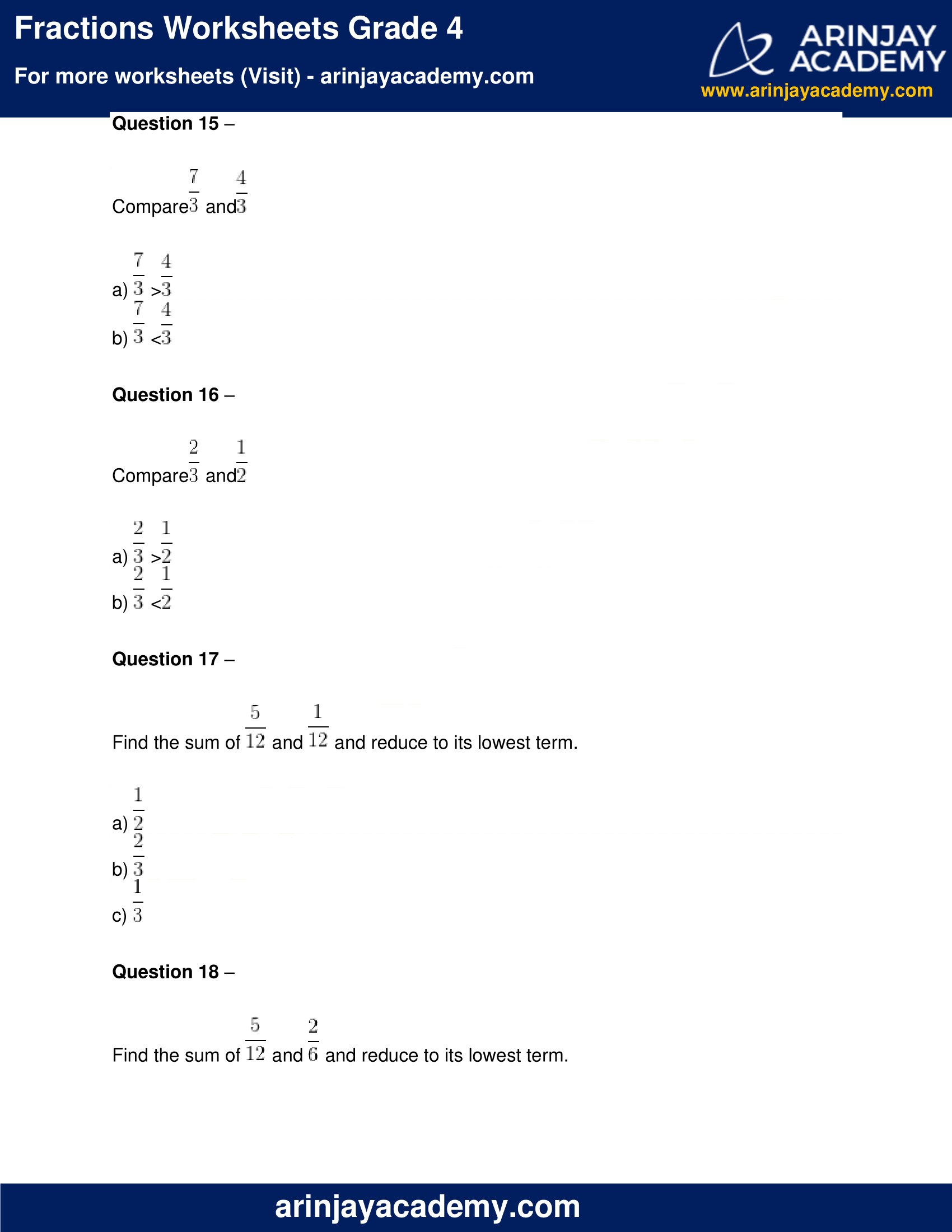
Fractions Worksheets Grade 4

Question 1 –

Fraction representing the Shaded part of the figure is?

a) $\cfrac{2}{5}$

b) $\cfrac{2}{4}$

Question 2

Is $\cfrac{3}{2}$ an Improper Fraction

a) Yes
b) No

Question 3 –

Is $\cfrac{3}{4}$ a proper Fraction

a) Yes
b) No

Question 4 –

Are the following Fractions are Like Fractions or Unlike Fractions?

$\cfrac{2}{3}$ , $\cfrac{3}{4}$ and $\cfrac{4}{5}$

a) Like Fractions
b) Unlike Fractions

Question 5 –

Is $\cfrac{1}{2}$ is a Unit Fraction ?

a) Yes
b) No

Question 6 –

Find : $\cfrac{7}{6}$ of 24

a) 21
b) 14
c) 28

Question 7 –

Find $\cfrac{4}{5}$ of an hour ?

a) 50 minutes
b) 45 minutes
c) 48 minutes

Question 8 –

Check whether $\cfrac{3}{4}$ and $\cfrac{9}{16}$ are Equivalent Fractions ?

a) Yes
b) No

Question 9 –

Write an equivalent Fraction of $\cfrac{20}{24}$ with denominator 6 .

a) $\cfrac{6}{4}$
b) $\cfrac{4}{6}$
c) $\cfrac{5}{6}$

Question 10 –

Write an equivalent Fraction of $\cfrac{2}{3}$ with Numerator 4 .

a) $\cfrac{4}{6}$
b) $\cfrac{4}{8}$
c) $\cfrac{8}{4}$

Question 11 –

Express $\cfrac{14}{7}$ as a whole number.

a) 2
b) 1
c) 4

Question 12 –

Convert $\cfrac{24}{20}$ into its simplest form.

a) $\cfrac{5}{4}$
b) $\cfrac{7}{6}$
c) $\cfrac{6}{5}$

Question 13 –

Convert $\cfrac{3}{2}$ into Mixed Fraction.

a) 1 $\cfrac { 1 }{ 2 }$
b) 2 $\cfrac { 1 }{ 2 }$
c) 3 $\cfrac { 1 }{ 2 }$

Question 14 –

Convert the Fraction $5\cfrac { 2 }{ 3 }$ into an Improper Fraction

a) $\cfrac { 18 }{ 3 }$
b) $\cfrac { 3 }{ 17 }$
c) $\cfrac { 17 }{ 3 }$

Question 15 –

Compare $\cfrac { 7 }{ 3 }$ and $\cfrac { 4 }{ 3 }$

a) $\cfrac { 7 }{ 3 }$ > $\cfrac { 4 }{ 3 }$
b) $\cfrac { 7 }{ 3 }$ < $\cfrac { 4 }{ 3 }$

Question 16 –

Compare $\cfrac { 2 }{ 3 }$ and $\cfrac { 1 }{ 2 }$

a) $\cfrac { 2 }{ 3 }$ > $\cfrac { 1 }{ 2 }$
b) $\cfrac { 2 }{ 3 }$ < $\cfrac { 1 }{ 2 }$

Question 17 –

Find the sum of $\cfrac{5}{12}$ and $\cfrac{1}{12}$ and reduce to its lowest term.

a) $\cfrac{1}{2}$
b) $\cfrac{2}{3}$
c) $\cfrac{1}{3}$

Question 18 –

Find the sum of $\cfrac{5}{12}$ and $\cfrac{2}{6}$ and reduce to its lowest term.

a) $\cfrac{2}{5}$
b) $\cfrac{3}{4}$
c) $\cfrac{1}{4}$

Question 19 –

Find the difference of $\cfrac{10}{6}$ and $\cfrac{7}{6}$ and reduce to its lowest term.

a) $\cfrac{3}{2}$
b) $\cfrac{1}{6}$
c) $\cfrac{1}{2}$

Question 20 –

Find the difference of $\cfrac{3}{4}$ and $\cfrac{1}{2}$ and reduce to its lowest term.

a) $\cfrac{1}{2}$
b) $\cfrac{1}{4}$
c) $\cfrac{3}{4}$

Fractions Worksheets Grade 4 Explanations

Q.1) Explanation – Fractions Worksheets Grade 4

As we know that a fraction represent a part of a whole.

Fraction of Shaded Part = $\cfrac { Shaded\quad part }{ Total\quad part }$

In the given figure,

Total part = 4

Shaded part = 2

Therefore,Fraction for the Shaded part = $\cfrac{2}{4}$

Correct Answer – b) $\cfrac{2}{4}$

Q.2) Explanation – Fractions Worksheets Grade 4

Improper Fractions, are a combination of Whole Number and a Proper Fraction. In an Improper Fraction, Numerator is greater than its Denominator

i.e Numerator > Denominator

In the given Fraction,

Numerator = 3

Denominator = 2

Here, 3 > 2

i.e, Numerator > Denominator

Hence, $\cfrac{3}{2}$ is an Improper Fraction

Correct Answer – a) Yes

Q.3) Explanation – Fractions Worksheets Grade 4

Proper Fraction, is a Fraction which represents the part of Whole Number. In Proper Fraction, Numerator is always less than its Denominator.

i.e Numerator < Denominator

In the given Fraction,

Numerator = 3

Denominator = 4

Here 3 < 4

i.e, Numerator < Denominator Hence, $\cfrac{3}{4}$ is a Proper Fraction.

Correct Answer – a) Yes

Q.4) Explanation – Fractions Worksheets Grade 4

In case of Like Fraction, the denominator of the Fractions are the same.

While, In case of Unlike Fraction denominator of the Fractions are different.

In the present case, the given Fractions are $\cfrac{2}{3}$ , $\cfrac{3}{4}$ and $\cfrac{4}{5}$

Since the Denominator in the present cases are 3 , 4 , 5 , which are not same, the given Fractions are Unlike Fractions

Correct Answer – b) Unlike Fractions

Q.5) Explanation – Fractions Worksheets Grade 4

Fractions with 1 as the numerator are called Unit Fractions.
Here, Numerator = 1
Hence, $\cfrac{1}{2}$ is a Unit Fraction

Correct Answer – a) Yes

Q.6) Explanation – Fractions Worksheets Grade 4

Step 1 : Divide the Whole Number by the denominator to get the Quotient.

24 ÷ 6 = 4

Step 2 : Multiply the Quotient by the Numerator.

4 x 7 = 28 Hence, $\cfrac{7}{6}$ of 24 = 28

Correct Answer – c) 28

Q.7) Explanation – Fractions Worksheets Grade 4

$\cfrac{4}{5}$ of an hour “means” $\cfrac{4}{5}$ of 60 minutes

i.e, ( $\cfrac{4}{5}$ x 60 ) minutes

Step 1 : Divide the Whole Number by the denominator to get the Quotient.

60 ÷ 5 = 12

Step 2 : Multiply the Quotient by the Numerator.

12 x 4 = 48

Hence, $\cfrac{4}{5}$ of an hour = 48 minutes

Correct Answer – c) 48 minutes

Q.8) Explanation – Fractions Worksheets Grade 4

If two fractions are equivalent, on cross multiplication, their Products will be the same

Cross multiplying $\cfrac{3}{4}$ and $\cfrac{9}{16}$ We get,

3 x 16 = 48

and

9 x 4 = 36

Since, the products are not same

Hence, $\cfrac{3}{4}$ and $\cfrac{9}{16}$ are not Equivalent Fractions.

Correct Answer – b) No

Q.9) Explanation – Fractions Worksheets Grade 4

Let,

$\cfrac{20}{24}$ = $\cfrac{?}{6}$

In order to obtain an equivalent fraction, we need to divide the Numerator and Denominator of a given number , by same digit

To get 6 in the denominator, we need to divide 24 by ( 24 ÷ 6 ) or 24 by 4

So, in order to get an equivalent Fraction, we have to divide the Numerator also by 4

i.e,

$\cfrac{20 \div 4 }{24 \div 4 }$ = $\cfrac{5}{6}$

Hence, $\cfrac{5}{6}$ is an equivalent Fraction of $\cfrac{20}{24}$ with denominator 6

Correct Answer – c) $\cfrac{5}{6}$

Q.10) Explanation – Fractions Worksheets Grade 4

Let,

$\cfrac{2}{3}$ = $\cfrac{4}{?}$

In order to obtain an equivalent fraction, we need to multiply the Numerator and Denominator of a given number , by same digit

To get 4 as Numerator, we have to multiply 2 by ( 4 ÷ 2 ) or 2 by 2

In order to get an equivalent Fraction, we have to multiply the Denominator by the same number, i.e, 2

i.e, $\cfrac { 2\times 2 }{3\times 2}$ = $\cfrac{4}{6}$

Hence, $\cfrac{4}{6}$ is an equivalent Fraction of $\cfrac{2}{3}$ with numerator 4

Correct Answer – a) $\cfrac{4}{6}$

Q.11) Explanation – Fractions Worksheets Grade 4

In order to convert an Improper Fraction to a Whole number, we have to divide Numerator by Denominator of the Fraction

Here, Numerator of Fraction = 14

Denominator of Fraction = 7

i.e, 14 ÷ 7 = 2

Hence, the required whole number is 2

Correct Answer – a) 2

Q.12) Explanation – Fractions Worksheets Grade 4

Given Fraction: $\cfrac{24}{20}$

In order to convert a fraction, into its simplest form, we first find the HCF of the Numerator and Denominator HCF of 24 and 20 is 4

Thereafter, we divide both the Numerator and Denominator by their HCF

i.e, 4 $\cfrac{24 \div 4 }{20 \div 4 }$ = $\cfrac{6}{5}$

Hence, $\cfrac{6}{5}$ is the simplest form of $\cfrac{24}{20}$

Correct Answer – c) $\cfrac{6}{5}$

Q.13) Explanation – Fractions Worksheets Grade 4

Given Fraction:

$\cfrac { 3 }{ 2 }$ Divide the Numerator by the Denominator

On dividing 3 by 2

We get Quotient = 1

Remainder = 1

For a Mixed Fraction we have to write ( Quotient + $\cfrac{Remainder}{Divisor}$ )

So, the Mixed Fraction is 1 + $\cfrac{1}{2}$ = 1 $\cfrac { 1 }{ 2 }$

Correct Answer – a) 1 $\cfrac { 1 }{ 2 }$

Q.14) Explanation – Fractions Worksheets Grade 4

A combination of Whole Number and a Proper Fraction is called a Mixed Fraction

Here,

Mixed Fraction = $5\cfrac { 2 }{ 3 }$

Whole Number Part = 5

Numerator = 2

Denominator = 3

Step 1 : Multiply the Whole Number Part and Denominator of the Mixed Fraction

5 x 3 = 15

Step 2 : Add the Numerator to the product obtained in Step 1

2 + 15 = 17

Write the sum as the numerator and denominator would remain the same , as in the Mixed Fraction.

$\cfrac { 17 }{ 3 }$

Hence, $5\cfrac { 2 }{ 3 }$ = $\cfrac { 17 }{ 3 }$

Correct Answer – c) $\cfrac { 17 }{ 3 }$

Q.15) Explanation – Fractions Worksheets Grade 4

$\cfrac { 7 }{ 3 }$ and $\cfrac { 4 }{ 3 }$ are Like Fraction as Denominator of both the Fractions is the same i.e, 3

In case of Like Fraction, the Fraction with the higher numerator is Higher

On Comparing the Numerators, we find

7 > 4

Hence, $\cfrac { 7 }{ 3 }$ > $\cfrac { 4 }{ 3 }$

Correct Answer – a) $\cfrac { 7 }{ 3 }$ > $\cfrac { 4 }{ 3 }$

Q.16) Explanation – Fractions Worksheets Grade 4

$\cfrac { 2 }{ 3 }$ and $\cfrac { 1 }{ 2 }$ are Unlike Fractions as Denominator of both the Fractions is different i.e, 3 and 2

To compare Unlike Fractions we have two methods:

First Method : By Converting Given Fractions into Like Fractions

Given Fractions : $\cfrac { 2 }{ 3 }$ and $\cfrac { 1 }{ 2 }$

Taking LCM of the Denominator of both the Fractions.

i.e, LCM of 3 and 2 is 6

To change the Unlike Fractions into Like Fractions

We have to multiply the Numerator and Denominator of the Given Fraction by a number such that the Denominator of the given Fraction becomes equal to its LCM i.e, 6

We have to multiply Numerator and Denominator of $\cfrac { 2 }{ 3 }$ i.e, 2 and 3 by $\cfrac { 6 }{ 3 }$ or 2

$\cfrac { 2\times 2 }{3\times 2}$ = $\cfrac{4}{6}$

We have to multiply Numerator and Denominator of $\cfrac { 1 }{ 2 }$ i.e, 1 and 2 by $\cfrac { 6 }{ 2 }$ or 3

$\cfrac { 1\times 3 }{2\times 3}$ = $\cfrac{3}{6}$

Now the Given Fractions are Like Fraction as their Denominator become same.

On Comparing their Numerators, we find 4 > 3

Therefore, $\cfrac { 4 }{ 6 }$ > $\cfrac { 3 }{ 6 }$ Hence, $\cfrac { 2 }{ 3 }$ > $\cfrac { 1 }{ 2 }$

Second Method : By Cross Multiplication Method

On Cross multiplying $\cfrac { 2 }{ 3 }$ and $\cfrac { 1 }{ 2 }$

In Cross Multiplication Method we multiply the Numerator of First Fraction namely 2 by the Denominator of Second Fraction namely 2

i.e, 2 x 2 = 4

Then, we multiply the Numerator of Second Fraction namely 1 by the Denominator of First Fraction namely 3

i.e, 1 x 3 = 3

Since, 4 > 3

Therefore, $\cfrac { 2 }{ 3 }$ > $\cfrac { 1 }{ 2 }$

Correct Answer – a) $\cfrac { 2 }{ 3 }$ > $\cfrac { 1 }{ 2 }$

Q.17) Explanation – Fractions Worksheets Grade 4

Sum of Like Fraction = $\cfrac { Sum\quad of\quad their\quad Numerators }{ Common\quad Denominator }$

= $\cfrac{5+1}{12}$ = $\cfrac{6}{12}$

Hence, the sum of $\cfrac{5}{12}$ and $\cfrac{1}{12}$ is $\cfrac{6}{12}$

Simplifying further,

HCF of 6 and 12 is 6

Dividing both Numerator and Denominator by their HCF i.e,

$\cfrac{6 \div 6 }{12 \div 6 }$ = $\cfrac{1}{2}$

Hence, the sum of $\cfrac{5}{12}$ and $\cfrac{1}{12}$ = $\cfrac{1}{2}$

Correct Answer – a) $\cfrac{1}{2}$

Q.18) Explanation – Fractions Worksheets Grade 4

In order to add Unlike Fraction

Firstly, we have to change the Unlike Fraction, into equivalent Like Fractions, and then add the two equivalent Like Fractions

Take LCM of 12 and 6 is 12

Converting the Unlike Fraction into Equivalent Like Fraction

We have to multiply , both the numerator and denominator of $\cfrac{5}{12}$ by 1

$\cfrac { 5\times 1 }{12\times 1}$ = $\cfrac{5}{12}$

We have to multiply , both the numerator and denominator of $\cfrac{2}{6}$ by 2

$\cfrac { 2\times 2 }{6\times 2}$ = $\cfrac{4}{12}$

Now $\cfrac{5}{12}$ + $\cfrac{4}{12}$ = $\cfrac{9}{12}$

Simplifying further,

HCF of 9 and 12 is 3

Dividing both Numerator and Denominator by their HCF

i.e, $\cfrac{9 \div 3 }{12 \div 3 }$ = $\cfrac{3}{4}$

Hence, the sum of $\cfrac{5}{12}$ and $\cfrac{2}{6}$ = $\cfrac{3}{4}$

Correct Answer – b) $\cfrac{3}{4}$

Q.19) Explanation – Fractions Worksheets Grade 4

Difference of Like Fraction = $\cfrac { Difference\quad of\quad their\quad Numerators }{ Common\quad Denominator }$

= $\cfrac{10 - 7}{6}$ = $\cfrac{3}{6}$

Simplifying further,

HCF of 3 and 6 is 3

Dividing both Numerator and Denominator by their HCF i.e, $\cfrac{3 \div 3 }{6 \div 3 }$ = $\cfrac{1}{2}$

Hence, the difference of $\cfrac{10}{6}$ and $\cfrac{7}{6}$ = $\cfrac{1}{2}$

Correct Answer – c) $\cfrac{1}{2}$

Q.20) Explanation – Fractions Worksheets Grade 4

To find the difference of Unlike Fraction

Firstly, we have to change the Unlike Fraction into equivalent Like Fraction, and then subtract the two equivalent Like Fraction

Take LCM of 4 and 2 is 4

Converting the Unlike Fraction into Equivalent Like Fraction

We have to multiply Numerator and Denominator of $\cfrac{3}{4}$ by 1

$\cfrac { 3\times 1 }{4\times 1}$ = $\cfrac{3}{4}$

We have to multiply Numerator and Denominator of $\cfrac{1}{2}$ by 2

$\cfrac { 1\times 2 }{2\times 2}$ = $\cfrac{2}{4}$

Now $\cfrac{3}{4}$ – $\cfrac{2}{4}$ = $\cfrac{1}{4}$

Hence, the difference of $\cfrac{3}{4}$ and $\cfrac{1}{2}$ = $\cfrac{1}{4}$

Correct Answer – b) $\cfrac{1}{4}$

Maths Worksheets for Class 4

Fractions Worksheets Grade 4

Fractions Worksheets Grade 4

Fractions Worksheets Grade 4 Explanations

Worksheets for Class 4

CBSE Notes for Class 4

Leave a Comment Cancel reply