NCERT Solutions for Class 8 Maths Chapter 11 Exercise 11.4 Mensuration has been designed by the NCERT to test the knowledge of the student. Class 8th maths exercise 11.4 contains 8 questions and each question has explained stepwise. If you are class 8th student you must be looking for the class 8th maths exercise 11.4 solutions for your exams preparation. Here we are providing complete NCERT solutions for class 8 maths chapter 11 exercise 11.4.
NCERT Solutions for Class 8 Maths Chapter 11 Exercise 11.4
- – Cuboid
– Cube
– Cylinders - Volume and Capacity
NCERT Solutions for class 8th maths exercise 11.4 chapter 11 Mensuration
1. Given a cylindrical tank, in which situation will you find surface area and in which situation volume.
(a) To find how much it can hold.
Sol.: – To find how much it can hold; we need to find VOLUME of the cylindrical tank.
(b) Number of cement bags required to plaster it.
Sol.: – To find Number of cement bags required to plaster it, we need to calculate SURFACE AREA of the cylindrical tank.
(c) To find the number of smaller tanks that can be filled with water from it.
Sol.: – To find the number of smaller tanks that can be filled with water from it, we need to find VOLUME of the cylindrical tank.
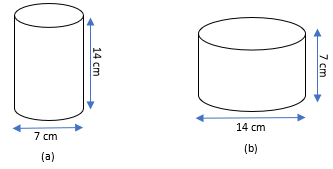
2. Diameter of cylinder A is 7 cm, and the height is 14 cm. Diameter of cylinder B is 14 cm and height is 7 cm. Without doing any calculations can you suggest whose volume is greater? Verify it by finding the volume of both the cylinders. Check whether the cylinder with greater volume also has greater surface area?
Sol.: – We know that,
Volume of cylinder = ?r2h
And, Surface area of cylinder = 2?r (r + h)
Volume of fig. (a) = (22/7) × 3.52 × 14
=539 cm3
Surface area of fig. (a) = 2 × (22/7) × 3.5 × (3.5 + 14)
= 385 cm2
Volume of fig. (b) = (22/7) × 72 × 7
= 1078 cm3
Surface area of fig. (b) = 2 × (22/7) × 7 × (7 + 7)
= 616 cm2
As we observe that, Volume and Surface area of figure (b) is higher than (a).
3. Find the height of a cuboid whose base area is 180 cm2 and volume is 900 cm3?
Sol.: –
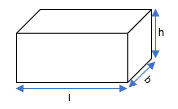
Let, Length of Cuboid = l,
Breadth of Cuboid = b,
And, Height of Cuboid = h
Given,
Area of base = 180 cm2
Volume of cuboid = 900 cm3
As, Area of base = 180 cm2
l × b = 180 .. (eq. 1)
And, Volume of cuboid = 900 cm3
l × b × h = 900
180 × h = 900 .. (From eq. 1)
So, h = 900/180 = 5 cm
So, Height of given cuboid is 5 cm.
4. A cuboid is of dimensions 60 cm × 54 cm × 30 cm. How many small cubes with side 6 cm can be placed in the given cuboid?
Sol.: – Since cube is to be placed inside cuboid.
So, Volume of cuboid = Number of cubes × Volume of one cube
Number of cubes = (Volume of cuboid/Volume of one cube)
Volume of cuboid = l × b × h
Where, l = Length = 60 cm
b = Breadth = 54 cm
h = Height = 30 cm
Volume of cuboid = 60 × 54 × 30
= 97200 cm3
Volume of one cube = a3
Where, a = Side = 6 cm
So, Volume of one cube = 63
= 216 cm3
Number of cubes = 97200/216
= 450 cubes
Therefore, 450 small cubes can be placed in the given cuboid.
5. Find the height of the cylinder whose volume is 1.54 m3 and diameter of the base is 140 cm?
Sol.: –
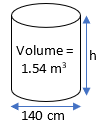
Volume of cylinder = 1.54 m3 = ?r2h
Where, r = Radius = Diameter/2 = (140/2) = 70 cm = (70/100) = 0.7 m
h = Height
Volume of cylinder = 1.54 = (22/7) × 0.72 × h
On solving this equation, we get
h = (1.54 × 7)/(22 × 0.7 × 0.7) = 1 m
So, Height of the cylinder is 1 m.
6. A milk tank is in the form of cylinder whose radius is 1.5 m and length is 7 m. Find the quantity of milk in litres that can be stored in the tank?
Sol.: – Radius of milk tank = 1.5 m
Length of milk tank = 7 m
So, Volume of tank = ?r2h
= (22/7) × 1.52 × 7
= 49.5 m3
= 49500 L .. (As 1 m3 = 1000 L)
So, quantity of milk that can be stored in the tank is 49500 L.
7. If each edge of a cube is doubled,
(i) How many times will its surface area increase?
Sol.: – We know that,
Surface area of cube = 6 a2
Where a = Length of edges of cube
When we doubled the length of edge of cube,
i.e. a = 2a
So, New surface area = 6 (2a)2
= 6 x 4 x a2
So, surface area becomes four time of original area when length of edge of cube is doubled.
(ii) How many times will its volume increase?
Sol.: – We know that,
Volume of cube = a3
After the length of edge of cube is doubled,
New Volume of cube = (2a) 3
= 8 a3
So, Volume becomes eight time of original when length of edge of cube is doubled.
8. Water is pouring into a cubiodal reservoir at the rate of 60 litres per minute. If the volume of reservoir is 108 m3, find the number of hours it will take to fill the reservoir.
Sol.: – Total capacity of reservoir = 108 m3
= 108000 L .. (As 1 m3 = 1000 L)
Water is coming in the reservoir at the rate of 60 litres per minute
So, Time taken to fill the tank = (Total capacity of reservoir/Rate at which water is coming in the reservoir)
= 108000/60
= 1800 minutes
= 30 Hours
So, Time taken to fill the reservoir is 30 Hours.
NCERT Solutions for class 8 Maths chapter 11
- Exercise 11.1 – Mensuration
- Exercise 11.2 – Mensuration
- Exercise 11.3 – Mensuration
- Exercise 11.4 – Mensuration
