NCERT Solutions for Class 8 Maths Chapter 11 Exercise 11.2 Mensuration

NCERT Solutions for Class 8 Maths Chapter 11 Exercise 11.2 Mensuration, has been designed by the NCERT to test the knowledge. Class 8 maths chapter 11 exercise 11.2 contains 5 questions and each question has explained in detail. If you are a class 8th student you must be looking for ncert solutions for maths class 8 chapter 11 exercise 11.2. Here We are providing the best quality ncert solutions for class 8 maths chapter 11 exercise 11.2. These solutions may help you to get good marks in your exams.

NCERT solutions for class 8 maths chapter 11 exercise 11.2

of the student on the following topics:-

• Area of Trapezium
• Area of a General Quadrilateral
  – Area of special quadrilaterals
• Area of a Polygon

NCERT Solutions for Class 8 Maths Chapter 11 Exercise 11.2 Mensuration

1. The shape of the top surface of a table is a trapezium. Find its area if its parallel sides are 1 m and 1.2 m and perpendicular distance between them is 0.8 m.

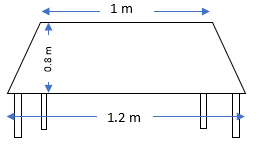
Sol.: – Area of table = (1/2) x h(a+b)
Where, h = distance between two parallel sides = 0.8 m
a = One of the parallel sides of the trapezium = 1 m
b = other parallel sides of the trapezium = 1.2 m

Area of table = (1/2) x 0.8 x (1 + 1.2)
= 0.88 m²

2. The area of a trapezium is 34 cm² and the length of one of the parallel sides is 10 cm and its height is 4 cm. Find the length of the other parallel side.

Sol.: – Area of trapezium = (1/2) x h(a+b)

Where, h = distance between two parallel sides = 4 cm
a = One of the parallel sides of the trapezium = 10 cm
b = other parallel sides of the trapezium

34 = (1/2) x 4 x (10+b)

After solving his equation, we get
b = [(34 x 2)/4] – 10 = 7 cm

So, length of other side of trapezium = 7 cm

3. Length of the fence of a trapezium shaped field ABCD is 120 m. If BC = 48 m, CD = 17 m and AD = 40 m, find the area of this field. Side AB is perpendicular to the parallel sides AD and BC.

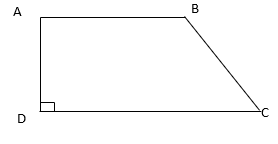
Sol.: – Length of the fence of a trapezium ABCD = AB + BC + CD + AD
120 = AB + 48 + 17 +40
So, AB = 15 m.

Area of trapezium = (1/2) × sum of parallel side×height between them
=(1/2)×(AD+BC)×AB
=(1/2)×(40+48)×15
= 660 m²

4. The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.

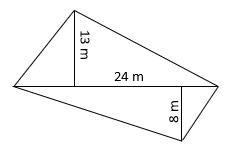
Sol.: – Area of quadrilateral = (1/2) × d × (h₁ + h₂)

Where d = Length of Diagonal = 24 m
h₁ and h₂ = Height from opposite vertices on diagonal = 13 m and 8 m.

So, Area of quadrilateral shaped field = (1/2)×24×(13+8)
= 252 m²

5. The diagonals of a rhombus are 7.5 cm and 12 cm. Find its area.

Sol.: – Area of Rhombus = (1/2) × d₁ × d₂
Where d₁ and d₂ = Length of diagonals = 7.5 cm and 12 cm

So, Area of Rhombus = (1/2) × 7.5 × 12
= 45 cm²

6. Find the area of a rhombus whose side is 6 cm and whose altitude is 4 cm. If one of its diagonals is 8 cm long, find the length of the other diagonal.

Sol.: – We know that,
Area of Rhombus = side × altitude
= 6 × 4
= 24 cm²

Also, Area of Rhombus = (1/2) × d₁ × d₂
Where d₁ and d₂ = Length of diagonals

So, Area of Rhombus = 24 = (1/2) × 8 × d₂
On solving this we get d₂ = 6 cm
So, Length of other diagonal = 6 cm.

7. The floor of a building consists of 3000 tiles which are rhombus shaped and each of its diagonals are 45 cm and 30 cm in length. Find the total cost of polishing the floor, if the cost per m² is Rs 4.

Sol.: – Diagonals of each rhombus d₁ and d₂ = 45 cm and 30 cm
So, Area of each rhombus shaped tiles = (1/2) × d₁ × d₂
= (1/2) × 45 × 30
= 675 cm²

As there are 3000 tiles on the floor.
So, Total area of floor = Area of one tile × Total number of tiles
= 675 × 3000
= 2025000 cm²
= (2025000/10000) m² (As 1 m² = 10000 cm²)
= 202.5 m²

So, total cost of polishing the floor = Total area of floor × Cost of polishing per m²
= 202.5 × 4
= ₹ 810

8. Mohan wants to buy a trapezium shaped field. Its side along the river is parallel to and twice the side along the road. If the area of this field is 10500 m² and the perpendicular distance between the two parallel sides is 100 m, find the length of the side along the river.

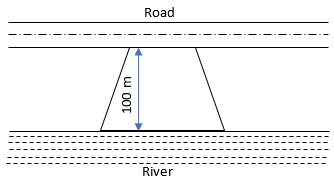
Sol.: – Given, Distance between the two parallel sides, h = 100 m
Area of the trapezium shaped field = 10500 m²

Let, Length of field along road side = L
So, Length of field along river side = 2L (given in question)

As we know that,
Area of trapezium = (1/2)×sum of parallel side × Distance between parallel sides
10500 = (1/2) x (L + 2L) × 100
On solving this equation, we get,
3L = [(10500 x 2)/100]
L = 210/3
L =  70 m
So, length of side along river = 2L = 2 × 70 = 140 m

9. Top surface of a raised platform is in the shape of a regular octagon as shown in the figure. Find the area of the octagonal surface.

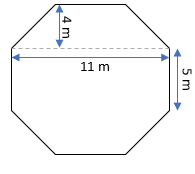
Sol.: – We can think of the given figure as three separate figures as below

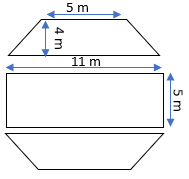
As we can see, we get two trapezium and one rectangle.
Now, the area of Octagonal figure
= 2 × Area of trapezium + Area of rectangle
= 2 × (1/2) × 4 × (5+11) + 11 ×5
= 64 + 55
= 119 m²

10. There is a pentagonal shaped park as shown in the figure. For finding its area Jyoti and Kavita divided it in two different ways.

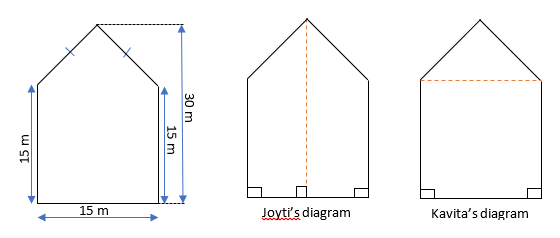
Find the area of this park using both ways. Can you suggest some other way of finding its area?

Sol.: – Area by Joyti’s diagram

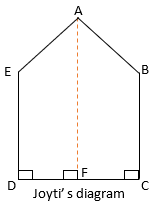
We can see that there are two trapeziums forming in the figure.
So, Area of Pentagon = Area of trapezium (ABCF + AEDF)
= 2 × Area of trapezium ABCF
=2× (1/2)×sum of parallel side × Distance between parallel sides
= 2 × (1/2) × (15/2) × (15 + 30)
= 337.5 m²

Area by Kavita’s diagram

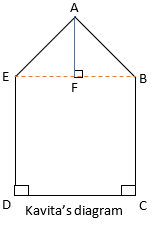
As we can see from Kavita’s figure, one square and one triangle is forming.
So, Area of Pentagon = Area of ABE + Area of square BCDE
= (1/2) × base × height + side²
= (1/2) × BE × AF + (CD)²
= (1/2) × 15 ×15 + 15²
=112.5 + 225
=337.5 m²

11. Diagram of the adjacent picture frame has outer dimensions =24 cm × 28 cm and inner dimensions 16 cm × 20 cm. Find the area of each section of the frame, if the width of each section is same.

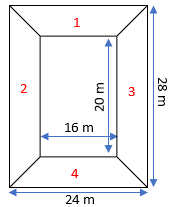
Sol.: – We can observe from the figure that, area of frame (1) = (4) and (2) = (3).
(As dimensions are equal for both figure)

Also, Height between any two-parallel sides = (24-16)/2 or (28-20)/2 = 4 m
(It will be same for all frame as mentioned in question)

So, Area of frame (1) or (4) = (1/2) × 4 × (16 + 24)
= 80 m²

And Area of frame (2) or (3) = (1/2) ×4 × (20 + 28)
= 96 m²

NCERT Solutions for maths class 8 chapter 11 Mensuration

• Exercise 11.1 – Mensuration
• Exercise 11.2 – Mensuration
• Exercise 11.3 – Mensuration
• Exercise 11.4 – Mensuration

Download NCERT Solutions for class 8 maths chapter 11 exercise 11.2 – Mensuration