NCERT Solutions for Class 8 Maths Chapter 11 Exercise 11.1 Mensuration, has been designed by the NCERT to test the knowledge of the student on the topic – Mensuration Introduction. Class 8 math exercise 11.1 contains 5 questions and each question has explained in detail. If you are a class 8th student you must be looking for ncert solutions for class 8 maths chapter 11 exercise 11.1. Here We are providing the best quality class 8 math exercise 11.1 solutions. These solutions may help you to get good marks in your exams.
NCERT Solutions for Class 8 Maths Chapter 11 Exercise 11.1 Mensuration
1. A square and a rectangular field with measurements as given in the figure have the same perimeter. Which field has a larger area?
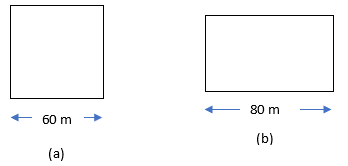
Sol.: – We know that,
Area of Square = (Side)2
Area of Rectangular = Length × Breadth
As we don’t know Breadth of Rectangle, we need to find it first to calculate area.
We know that,
Perimeter of square = Perimeter of rectangular, (Mentioned in question)
Also,
Perimeter of square = Sum of all side = 4 × Side, And
Perimeter of rectangular = 2 × (Length + Breadth)
So,
4 × Side = 2 × (Length + Breadth)
4 × 60 = 2 × (80 + Breadth)
After solving this equation, we get
Breadth = [(4×60)/2] – 80
= 40m
Area of Square = (Side)2 = (60)2 = 60 × 60 = 3600 m2
And, Area of Rectangle = Length × Breadth = 40 × 80 = 3200 m2
Therefore, area of Square field is larger than Rectangular field.
2. Mrs. Kaushik has a square plot with the measurement as shown in the figure. She wants to construct a house in the middle of the plot. A garden is developed around the house. Find the total cost of developing a garden around the house at the rate of Rs 55 per m2.
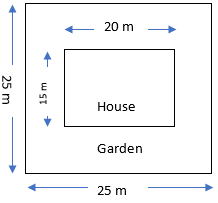
Sol.: – Area of garden = Area of Total plot – Area of house
= 25 × 25 – 15 × 20
= 625 – 300
=325 m2
 So, total cost of developing a garden around the house
= Total Area of garden × Cost of developing the garden per m2
= 325 × 55
= ₹ 17875
3. The shape of a garden is rectangular in the middle and semi circular at the ends as shown in the diagram. Find the area and the perimeter of this garden [Length of rectangle is 20 – (3.5 + 3.5) metres].
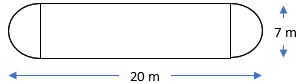
Sol.: – As we can see in the figure,
Perimeter of the garden = Perimeter of rectangle × perimeter of semi-circle
= (2 × Length of rectangle) + (2 × π × Radius of circle)
(Here, Length of rectangle = 20 – (3.5 + 3.5) = 13 m)
(Here, Radius of circle = 7/2 = 3.5 m)
So, Perimeter of the garden = (2 x 13) + (2 x (22/7) x 3.5)
= 26 + 22
= 48 m
And, Area of the garden = Area of rectangle + 2 × Area of semi-circle
= (Length × Breadth) + 2 × (πr²/2)
= (13 × 7) + 2 × (22×3.5²/2×7)
= 91 + 38.5
=129.5 m2
4. A flooring tile has the shape of a parallelogram whose base is 24 cm and the corresponding height is 10 cm. How many such tiles are required to cover a floor of area 1080 m2? (If required you can split the tiles in whatever way you want to fill up the corners).
Sol.: – We know that,
Area of parallelogram = Base × Height
= 24 × 10
= 240 cm2
Area of floor = 1080 m2
= 1080 × 10000 m2 (As 1m2= 10000 cm2 )
= 10800000 m2
 So, Number of tiles required to cover the floor = (Area of floor/Area of parallelogram)
= 10800000/240
= 45000 tiles
5. An ant is moving around a few food pieces of different shapes scattered on the floor. For which food-piece would the ant have to take a longer round? Remember, circumference of a circle can be obtained by using the expression c = 2Ï€r, where r is the radius of the circle.
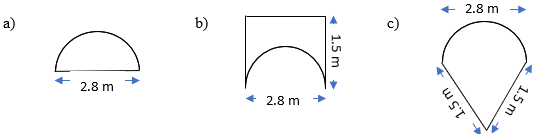
Sol.: – For checking on which food-piece the ant would take longer round; we need to find Perimeter of all food-piece.
a). Perimeter of 1st food-piece = circumference of semi-circle + D
= πr + D
= [(22 × 1.4)/7] + 2.8
= 7.2 cm
b). Perimeter of 2nd food-piece = circumference of semi-circle + 3 sides of rectangle
= [(22 × 1.4)/7] + 1.5 +1.5 +2.8
= 10.2 cm
c). Perimeter of 3rd food-piece = circumference of semi-circle + 2 sides of triangle
= [(22 × 1.4)/7] + 2 + 2
= 8.4 cm
Therefore, Perimeter of food piece (b) is largest. So, ‘Ant’  will take longest round around food piece (b).
NCERT Solutions for class 8 maths chapter 11 exercise 11.1
- Exercise 11.1 – Mensuration
- Exercise 11.2 – Mensuration
- Exercise 11.3 – Mensuration
- Exercise 11.4 – Mensuration
Download NCERT Solutions for Class 8 Maths Chapter 11 Exercise 11.1 Mensuration
