NCERT Solutions For Class 10 Maths Chapter 6 Exercise 6.3 Triangles

NCERT Solutions For Class 10 Maths Chapter 6 Exercise 6.3 Triangles

Download NCERT Solutions For Class 10 Maths Chapter 6 Exercise 6.3 Triangles. This Exercise contains 16 questions, for which detailed answers have been provided in this note. In case you are looking at studying the remaining Exercise for Class 10 for Maths NCERT solutions for other Chapters, you can click the link at the end of this Note.

Category	NCERT Solutions for Class 10
Subject	Maths
Chapter	Chapter 6
Exercise	Exercise 6.3
Chapter Name	Triangles

NCERT Solutions For Class 10 Maths Chapter 6 Exercise 6.3 Triangles

1. State which pair of triangles in the figures are similar. Write the similarity criterion used by you for answering the equation and also write the pair of similar triangles in the symbolic form.

(i)

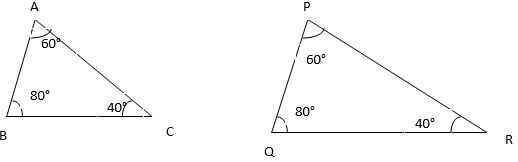
Solution:

In ∆ABC and ∆PQR we have,
∠A = ∠P = 60°
∠B = ∠Q = 80°
∠C = ∠R = 40°
∆ABC∼∆PQR  [By AAA similarity criteria]

 

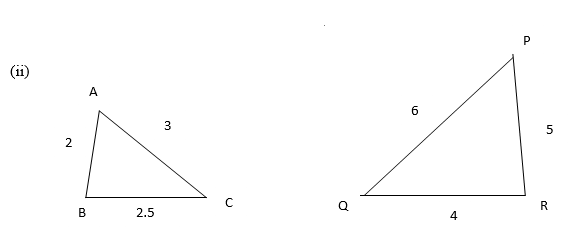
Solution:

Here  = = , = = and = =

Since corresponding sides are proportional, then by SSS similarity criteria ∆ABC∼∆QRP

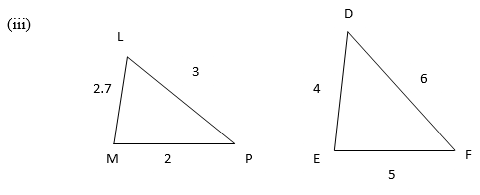
Solution: Corresponding sides of the given triangles are not proportional. Hence the given two triangles are not similar.

(iv)

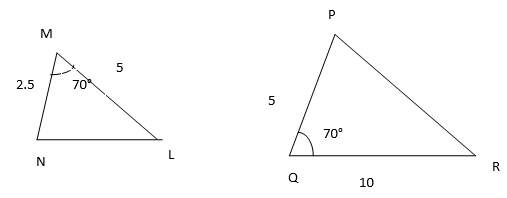
Solution: Corresponding sides of the given triangles are not proportional. Hence the given two triangles are not similar.

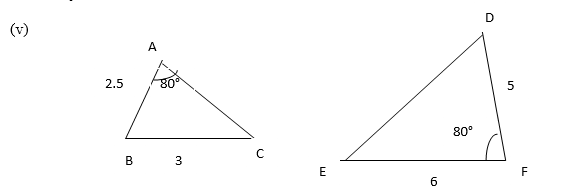
Solution: The ratio of AB and DF is and that of the sides BC and EF is . But the corresponding angle is not contained by the corresponding sides. Hence these two triangles are not similar.

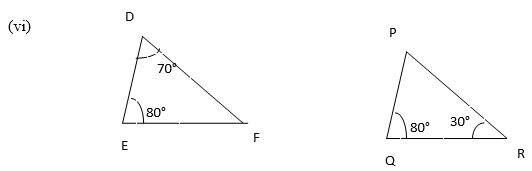
Solution: We know that sum of the angles of a triangle is 180°.
In ∆DEF, ∠D = 70°, ∠E = 80°
∴ ∠F = 180°-(70°+80°) = 30°
In ∆PQR, ∠Q = 80°, ∠R =30°
∴ ∠P = 180°-(80°+30°) = 180°-110° = 70°
In ∆DEF and ∆PQR
∠D = ∠P = 70°
∠E = ∠Q = 80°
∠F = ∠R = 30°
∆DEF∼∆PQR  [By AAA similarity criterion]

 

2. In the figure ∆ODC ∼∆OBA, ∠BOC = 125° and ∠CDO = 70°. Find ∠DOC, ∠DCO, and ∠OAB.

 

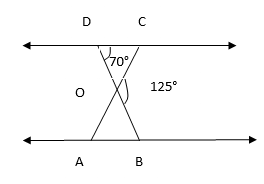
Solution:

∠DOC+∠BOC = 180° [ Linear pair of Angles ]
∠DOC+125° = 180°
∴∠DOC = 55°
By using Angle sum property, In ∆DOC
∠DOC+∠ODC+∠DCO = 180°
55°+70°+∠DCO = 180°
125°+∠DCO = 180°
∴∠DCO = 55°
Since ∆ODC ∼∆OBA and corresponding angles are equal in a similar triangle, therefore
∠OAB =∠DCO = 55°
∴∠OAB = 55°

3. Diagonal AC and BD of a trapezium ABCD with AB||DC intersect each other at the point O. Using a similarity criterion for two triangles, show that =

Solution:

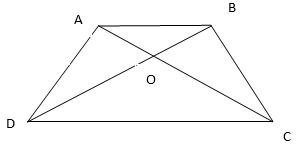
In ∆ABO and ∆DOC, AB||DC
∠BOA = ∠DOC [Vertical opposite angles]
∠OAB = ∠OCD [Alternate interior angles]
∠OBA = ∠ODC [Alternate interior angles]
∆ABO∼∆DOC [ By AAA similarity criteria]
=   [Corresponding sides are proportional]
=

 

4. In the figure =  and ∠1= ∠2. Show that ∆PQS∼∆TQR.

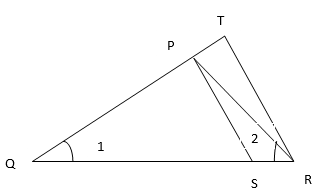
Solution:
In ∆PQR, ∠PQR = ∠PRQ
PQ=PR……..(1) (Sides opposite to equal angles are also equal)
Given that = …….(2)
Substitute the value of equation (1) in the equation (2) we have
=
In ∆PQS and ∆TQR
= [From equation 2]
∠PQS = ∠TQR [Common]
∆PQS∼∆TQR [By SAS similarity criteria]

 

5. S and T are points on sides PR and QR of the ∆PQR such that ∠P = ∠RTS. Show that ∆RPQ∼∆RTS

Solution:

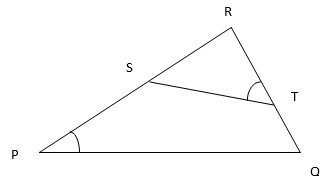
In ∆RPQ and ∆RTS
∠RPQ = ∠RTS [Given]
∠PRQ = ∠SRT [Common]
∆RPQ∼∆RTS  [By AA similarity criterion]

 

6. In the figure ∆ABE ≅ACD, show that ∆ADE∼∆ABC

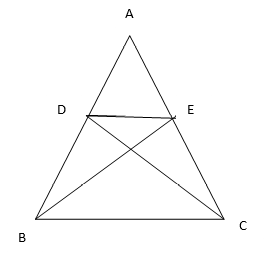
Solution:

Given ∆ABE ≅ACD, then
AB = AC…..(1)
AD = AE……(2)
Dividing equation (1) by equation (2) we have
=
In ∆ADE and ∆ABC
=
∠A = ∠A [Common]
∆ADE∼∆ABC [By SAS similarity criterion]

 

7. In the figure altitudes AD and CE of ∆ABC intersect each other at the point P.

 

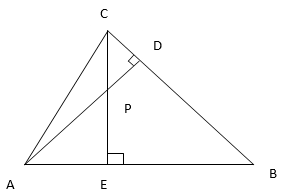
Show that

(i) ∆AEP∼∆CDP

Solution:

In ∆AEP and ∆CDP
∠APE=∠CPD (Vertically opposite angles)
∠AEC=∠CDE = 90°
∆AEP∼∆CDP [By AA similarity criterion]

(ii) ∆ABD∼∆CBE

Solution:

In ∆ABD and ∆CBE,
∠ABD = ∠EBC (Common)
∠ADB=∠BEC = 90°
∆ABD∼∆CBE [By AA similarity criterion]

(iii) ∆AEP∼∆ADB.

Solution:

In ∆AEP and ∆ADB.
∠AEP=∠ADB = 90°
∠PAE=∠DAB [Common]
∆AEP∼∆ADB [By AA similarity criterion]

(iv) ∆PDC∼∆BEC.

Solution:

In ∆PDC and ∆BEC
∠PCD=∠ECB [Common]
∠PDC=∠CEB = 90°
∆PDC∼∆BEC [By AA similarity criterion]

 

8. E is a point on the side AD produced on a parallelogram ABCD and BE intersects CD at F. Show that ∆ABE∼∆CFB.

Solution:

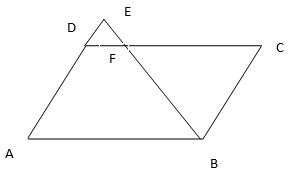
In ∆ABE and ∆CFB
∠EAB=∠FCB (Opposite angles of the parallelogram)
∠AEB=∠FBC (Since AE || BC, Alternate angles)
∆ABE∼∆CFB [By AA similarity criterion]

 

9. In the figure ABC and AMP are two right triangles, right-angled at B and M respectively.

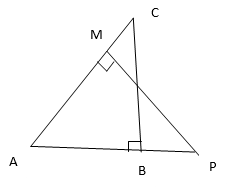
Prove that

(i) ∆ABC∼∆AMP.

Solution:

In ∆ABC and ∆AMP,
∠ ABC = ∠AMP= 90°
∠ CAB = ∠MAP [Common]
∆ABC∼∆AMP [By AA similarity criterion]

(ii) =

Solution:

Since ∆ABC∼∆AMP, then corresponding sides are proportional.
Therefore,  =

10. CD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ∆ABC and ∆EFG respectively. If ∆ABC∼∆FEG, show that

(i) =

(ii) ∆DCB∼∆HGE

(iii) ∆DCA∼∆HGF

Solution:

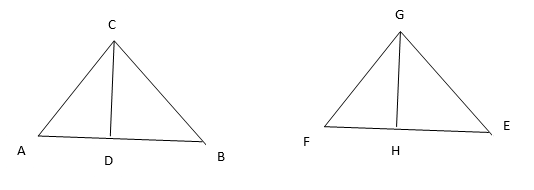
Given: In ∆ABC∼∆FEG
Then, ∠ACB= ∠FGE, ∠CAB=∠GFE and ∠ABC=∠FEG
Since, ∠DCA=∠FGH and ∠DCB=∠HGE (Angle bisector)

(i) In ∆ACD and ∆FGH
∠CAD=∠GFH [Given]
∠DCA=∠FGH [Proved above]
∆ACD∼∆FGH [By AA similarity criterion]
Hence, =

(ii) In ∆DCB and ∆HGE
∠DCB=∠HGE  [CD is the angle bisector]
∠DBC=∠HEG   [Given]
∆DCB∼∆HGE [By AA similarity criterion]

(iii) In ∆DCA and ∆HGF
∠DCA=∠FGH [CD is the angle bisector]
∠CAD=∠GFH [Given]
∆DCB∼∆HGF [By AA similarity criterion]

 

11. In figure E is a point on side CB produced of an isosceles triangle ABC with AB=AC. If AD⊥BC and EF⊥AC, prove that ∆ABD∼∆ECF.

 

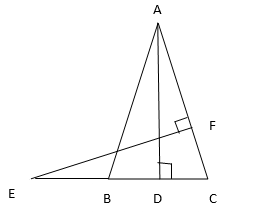
Solution:

Given: ∆ABC is isosceles triangle
AB=AC.
∠ABD= ∠ACB= ∠ACE…..(1)
In ∆ABD and ∆ECF,
∠ADB= ∠EFC= 90°
∠ABD= ∠FCE (From Equation (1))
∆ABD∼∆ECF  [By AA similarity criterion]

 

12. Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of triangle PQR. Show that ∆ABC∼∆PQR

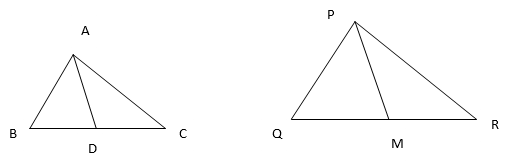
Solution: Since AD and PM are the median of ∆ABC and ∆PQR, then
BD = and QM = …….(1)
= = …..(2) [Given]
Hence = = (using (1))
= =   ……..(3)
In ∆ABD and ∆PQM
= = [From equation (3)]
∆ABD∼∆PQM [By SSS similarity criterion]
Therefore ∠ABD=∠PQM …..(3) (Corresponding angles of similar triangles)
In ∆ABC and ∆PQR
∠ABD=∠PQM (From Equation (3))
= (From Equation (2))
∆ABC∼∆PQR [By AA similarity criterion]

 

13. D is a point on the side BC of a triangle ∆ABC such that ∠ADC=∠ Show that CA²=CB.CD.

Solution:

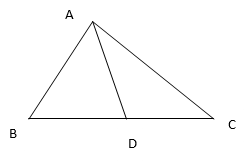
In ∆ADC and ∆BAC we have
∠ACD=∠BCA [Common]
∠ADC=∠BAC [Given]
∆ADC∼∆BAC [By AA similarity criterion]
Then, the corresponding sides are in proportion.
=
CA² = CB.CD

 

14. Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ∆ABC∼∆PQR.

Solution:

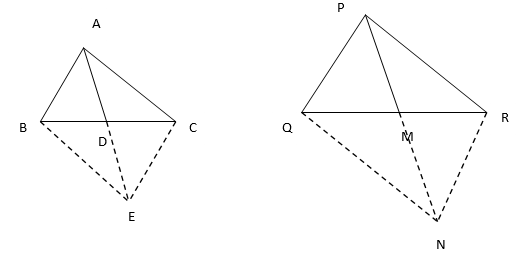
Given = = ……(1)
Let us extend AD and PM up to the point E and N respectively so that AD=DE and PM=MN
Join points B and E, C and E; Q and N, R and N.
Since AD and PM are the median of ∆ABC and ∆PQR respectively, then
BD=DC and QM=MR
Since, diagonal AE and BC of the quadrilateral ABEC bisect each other at D, then ABEC is parallelogram.
Hence AC=BE and AB=CE……(2)
Similarly, quadrilateral PQRN is parallelogram.
Therefore PR=QN and PQ=RN…..(3)
From equation (1), (2) and (3) we have
= =
= =
= =
∆ABE∼∆PQN [By SSS similarity criterion]
∴ ∠BAE=∠QPN …….(4)(as these are the corresponding angles of similar triangles)
Similarly, ∆AEC∼∆PNR
hence ∠CAE=∠RPN……(5)
Adding equation (4) and (5) we get
∠BAE + ∠CAE = ∠QPN + ∠RPN
∠BAC=∠QPR
In ∆ABC and ∆PQR.
∠BAC=∠QPR
=   (From equation (1))
∆ABC∼∆PQR [By SSS similarity criterion]

Exercise 6.3 class 10 NCERT solutions Chapter 6

15. The vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.

Solution:

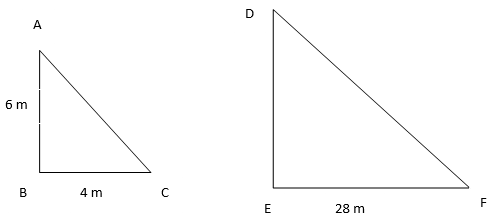
Let AB and DE be the pole and tower respectively and the shadow of AB be BC and shadow of DE be EF.
Hence AB= 6 m, BC=4 m, EF=28 m…..(1)
Since sun rays fall on the tower and the pole at the same angel at the same time.
∴ ∠BAC=∠EDF
∠BCA=∠EFD
Then, ∆ABC∼∆DEF [By AAA similarity criterion]
∴ =   [Corresponding sides of a similar triangle are same]
= (using (1))
DE =
DE = 42 m
Therefore, the height of the tower is 42 m.

 

16. If AD and PM are medians of triangles ABC and PQR, respectively where ∆ABC∼∆PQR, prove that =

Solution:

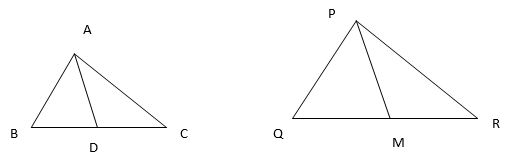
Given: ∆ABC∼∆PQR
Therefore, corresponding sides are in proportion.
= = …….(1) and
∠A=∠P, ∠B=∠Q and ∠C=∠R……..(2)
Since, AD and PM are medians of the triangles then
BC=2BD and QR=2QM……..(3)
From equation (1) and (3) we get
= =
=
In ∆ABD and ∆PQM
=
∠B=∠Q (From equation (2))
∆ABD∼∆PQM (by SAS similarity criterion)
= [Ratio of corresponding sides of similar triangle are same]

NCERT Solutions for Class 10 Maths Chapter 6 Exercise 6.3 Triangles, has been designed by the NCERT to test the knowledge of the student on the topic – Criteria for Similarity of Triangles

• NCERT Solutions For Class 10 Maths Chapter 6

  • NCERT Solutions Class 10 Maths Chapter 6 Ex. 6.1 Triangles
  • NCERT Solutions Class 10 Maths Chapter 6 Ex. 6.2 Triangles
  • NCERT Solutions Class 10 Maths Chapter 6 Ex. 6.3 Triangles
  • Maths – NCERT Solutions Class 10
  • NCERT Solutions Class 10

Download NCERT Solutions For Class 10 Maths Chapter 6 Exercise 6.3 Triangles