NCERT Solutions For Class 10 Maths Chapter 5 Exercise 5.2 Arithmetic Progressions
Download NCERT Solutions For Class 10 Maths Chapter 5 Exercise 5.2 Arithmetic Progressions. This Exercise contains 20 questions, for which detailed answers have been provided in this note. Arithmetic Progressions exercise 5.2 class 10 chapter 5 NCERT Solutions have been explained in a simple and easy-to-understand language to help you learn and prepare for your upcoming class 10 Maths exams. Here we are sharing Arithmetic Progressions ex 5.2 class 10 solution.
| Category | NCERT Solutions for Class 10 |
| Subject | Maths |
| Chapter | Chapter 5 |
| Exercise | Exercise 5.2 |
| Chapter Name | Arithmetic Progressions |
NCERT Solutions For Class 10 Maths Chapter 5 Exercise 5.2 Arithmetic Progressions
NCERT Solutions For Class 10 Maths Chapter 5 Exercise 5.2 – Arithmetic Progressions
A. Fill in the blanks in the following table, given that a is the first term, d the common difference, and an the nth term of the AP:
Solution : If a be the first term and d be the common difference of an AP then the nth term of that AP is given by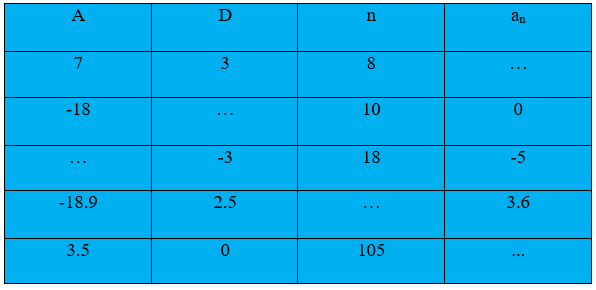
an = a+(n-1)d
(i) a = 7, d = 3, n = 8
Solution: We know that,
an = a + (n-1) d
= 7 + (8-1)×3
= 7 + 21
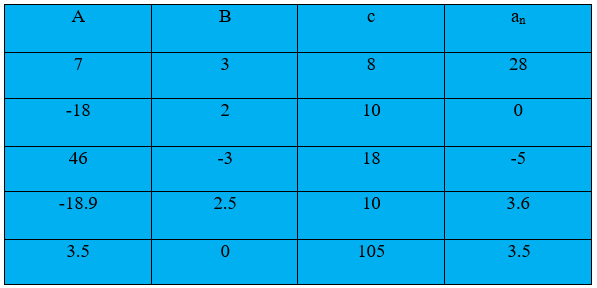
= 28
(ii) a = -18, n = 10, an = 0
Solution: We have,
an = a + ( n – 1 ) d
Substituting the given values in the above formula we get,
0 = -18 + (10-1) d
0 = -18 + 9d
18 =9d
d = 2
(iii) d = -3, n =18, an= -5
Solution: We know that,
an = a + (n-1) d
Substituting the given values in the above formula we get
– 5 = a + (18 – 1)×(- 3)
– 5 = a + 17 ×(- 3)
– 5 = a-51
a = 51-5
a = 46
(iv) a = – 18.9, d = 2.5, an = 3.6
Solution: We know the relation is
an= a + (n – 1)d
Substituting the given values in the above equation,
3.6 = -18.9+(n – 1) ×2.5
(n – 1)×2.5 = 3.6+18.9
(n – 1) ×2.5 = 22.5
n – 1= (22.5/2.5)
n – 1 = 9
n = 9 + 1
n = 10
(v) a = 3.5, d = 0, n =105
Solution: We know that,
an = a + (n – 1)d
Substituting the values in the above equation
an = 3.5 +( 105-1)×0
= 3.5 + 104×0
= 3.5 + 0
= 3.5
Answer
B. Choose the correct choice in the following and justify :
(i) 30th term of the AP: 10, 7, 4, . . . , is
(A) 97 (B) 77 (C) –77 (D) – 87
Solution: The AP is given by 10, 7, 4, …
First term, a = 10,
Common difference, d = 7 – 10 = – 3
We know that,
an = a + (n – 1) d
a30 = a + (30 – 1)×d
a30= 10 + (30 – 1)(- 3)
a30= 10 + 29× (-3)
a30= 10 – 87
a30= -77
Hence, the correct answer is option (C)
(ii) 11th term of the AP: – 3, (-1/2) , 2, . . ., is
(A) 28 (B) 22 (C) –38 (D) –48
Solution : AP is given by -3, (-1/2), 2, …
First term, a = -3
Common difference, d = (-1/2) – ( – 3 )
= (-1/2) + 3 = (5/2)
We know that,
an = a + (n – 1) d
a11= -3+(11-1)(5/2)
a11= – 3+10×(5/2)
a11= – 3+25
a11= 22
Hence, the correct answer is option (B)
3. In the following APs find the missing terms in the boxes:
(i) 2, ___, 26
Solution: In the given A.P.,
a = 2
a3 = 26
We know that,
an = a + (n – 1) d
a3 = 2 + (3 – 1) d
26 = 2 + 2d
24 = 2d
d = 12
a2 = a + d = 2 + 12 = 14
Hence the missing term is 14.
(ii) ___, 13, ___, 3
Solution: In the given AP, a2 =13 and a4 = 3
We know that,
an = a + (n – 1) d
a+d = 13….(1) and
a+3d = 3….(2)
On Subtracting equation (1) from equation (2), we get
2d = -10
d = -5
a = a2 – d = 13 – (-5) = 13 + 5 = 18
a3 = a2 + d = 13 + (-5) = 13 – 5 = 8
Hence the missing term are 18 and 8.
(iii) 5, ___, ___, 9 1⁄2
Solution: In the given AP, a = 5 and a4 = 9 1⁄2
We know that,
an = a + (n – 1) d
a4= a+(4-1)d
9 1⁄2 = 5+3d
3d = (19/2) -5
3d = (19/2)
d = 3/2
a2 = a + d = 5 + (3/2) = (13/2) = 6 1⁄2
a3 = a+2d = 5+ 2 3⁄2 = 5+3 = 8
Hence the missing terms are 6 and 8 respectively.
(iv) -4 , __, __, __, 6
Solution: In the given AP, a = -4 and a4 = 6
We know that,
an = a + (n – 1) d
a6= a+(6-1)d
6 = -4+5d
5d = 10
d = 2
Therefore,
a2 = a + d = -4+2 = -2
a3 = a+2d = -4+2×2 = -4+4 = 0
a4 = a+3d = -4+3×2 = -4+6 = 2
a5 = a+4d = -4+4×2 = -4+8 = 4
Therefore the missing terms are -2, 0, 2, 4
(v) __, 38, __, __, __, -22
Solution: In the given AP, a2 = 38 and a6 = -22
We know that,
an = a + (n – 1) d
a2= a+(2-1)d
38 = a+d
a+d = 38…..(1)
a6 = a+(6-1)d
-22 = a+5d
a+5d = -22…..(2)
On Subtracting equation (1) from equation (2) we get
4d = -60
d = -15
Substituting the value of d in the equation (1) we get
a-15 = 38
a = 53
Therefore
a3 = a+2d = 53+2×(-15) = 53-30 = 23
a4 = a+3d = 53+3×(-15) = 53-45 = 8
a5 = a+4d = 53+4×(-15) = 53-60 = -7
Therefore the missing terms are 53, 23, 8, -7 respectively.
Arithmetic Progressions NCERT Solutions For Class 10 Maths Chapter 5 Exercise 5.2
4. Which term of the AP: 3, 8, 13, 18, …, is 78?
Solution: Let 78 is the nth term of the given AP.
First term, a = 3
Common ratio, d = 8-3 = 5
We know that,
an = a + (n-1) d
78 = 3+(n-1)5
75 = (n-1)5
15 = n-1
n = 16
Hence, 16th term is of the given AP is 78.
5. Find the number of terms in each of the given APs.
(i) 7, 13, 19, …,205
Solution: Let the number of terms of the given AP is n.
First term, a =7
Common difference, d = 13-7 = 6.
an = 205
an = a + (n-1) d
205 = 7+(n-1)6
198 = (n-1)6
n-1 = 33
n = 34
Hence, the number of terms of the AP is 34.
(ii) 18, 15 1⁄2 , 13, …,.-47
Solution: Let the number of terms of the given AP is n.
First-term, a =18
Common difference, d = 15 1⁄2 – 18 = (31/2) – 18 = (-5/2)
As we know that,
an = a + (n-1) d
-47 = 18+(n-1)(-5/2)
-65 = (n-1)(-5/2)
(65×2)/5= n-1
26 = n -1
n = 27
Hence, the number of terms of the AP is 27.
6. Check whether -150 is a term of the AP: 11, 8, 5, 2,…
Solution: In the given AP,
First term, a = 11
Common difference d = 8-11 = -3
Let nth term of the given AP is -150.
As we know that,
an = a + (n-1) d
-150 = 11+(n-1)(-3)
-161 = (n-1)(-3)
n-1 = (161/3)
n = 1+(161/3), which is not possible because 1+(161/3) is not an integer value.
Hence, -150 is not a term of this AP.
7. Find the 31st term of an AP whose 11th term is 38 and the 16th term is 73.
Solution: Let a be the first term and d be the common difference of the AP.
As we know that,
an = a + (n-1) d
a11 = a + (11-1) d
38 = a + 10 d
a+10d = 38……(1) and
Similarly, a16 = a + (16-1) d
73 = a+15d
a+15d = 73……(2)
Subtracting the equation (1) from the equation (2) we get
5d = 35
d = 7
Substituting the value of d in the equation (1) we get
a+10×7 = 38
a+70 = 38
a = -32
Then, 31th term of the AP is
a31 = -32 + (31-1) 7
a31 = -32+210
a31 = 178.
Hence, the 31st term of the AP is 178.
8. An AP consists of 50 terms of which the 3rd term is 12 and the last term is 106. Find the 29th
Solution: Let a be the first term and d be the common difference of the AP.
As we know that,
an = a + (n-1) d
a3 = a + (3-1) d
12 = a+2d
a+2d = 12……(1) and
a50 = a + (50-1) d
106 = a+49d
a+49d = 106……(2)
Subtracting the equation (1) from (2) we get
47d = 94
d = 2
Substituting the value of d in the equation (1) we get
a+2×2 = 12
a+4 = 12
a = 8
Then, 29th term of the AP is,
a29 = 8+(29-1)2
a29 = 8+28×2
a29 = 64.
Hence, 29th term of the AP is 64.
9. If the 3rd and 9th terms of an AP are 4 and -8 respectively, which term of this AP is zero?
Solution: Let a be the first term and d be the common difference of the AP and nth term of this AP be zero.
Given:
a3 = 4
a9 = -8
As we know that,
an = a + (n-1) d
a3 = a + (3-1) d
4 = a+2d
a+2d = 4……(1)
a9 = a + (9-1) d
-8 = a + 8d
a+8d = -8……(2)
Subtracting the equation (1) from equation (2) we get
6d = -12
d = -2
Substituting the value of d in the equation (1) we get
a+2(-2) = 4
a-4 = 4
a = 8
If nth term of this AP is zero, then an = 0
As we know that,
an = a + (n-1) d
0 = 8+(n-1)(-2)
-(n-1)2 = -8
n-1 = 4
n = 5
Therefore the 5th term of this AP is zero.
10. The 17th term of an AP exceeds its 10th term by 7. Find the common difference.
Solution: Let a be the first term and d be the common difference of the AP.
As we know that,
an = a + (n-1) d
a17 = a + (17-1) d
a17 = a + 16d
Similarly, a10 = a + 9d
Then using the given condition we have,
a+16d = a+9d+7
7d = 7
d = 1
Therefore, the common difference of the AP is 1.
11. Which term of the AP: 3, 15, 27, 39, … will be 132 more than its 54th term
Solution: In the given AP,
First term, a = 3
Common difference, d = 15-3 = 12.
As we know that,
an = a + (n-1) d
a54 = 3 + (54-1) 12
a54 = 3 + 53 x 12
a54 = 3 + 636
a54 = 639
Let nth term of the given AP be 132 more than 54th term.
3+(n-1)12 = a54 + 132
3+(n-1)12 = 639 + 132
3+(n-1)12 = 771
(n-1)12 = 768
n-1 = 64
n = 65.
Hence, 65th term of this AP is 132 more than 54th term.
12. Two APs has the same common difference. The difference between their 100th terms is 100. What is the difference between their 1000th terms?
Solution: Let a and b be the first terms of the given two APs respectively and the common difference of both the APs is d.
As we know that,
an = a + (n-1) d
For 1st AP
a100 = a + (100-1) d
a100 = a + 99d
a1000 = a + (1000-1) d
a1000 = a + 999d
For 2nd AP
a100 = b + (100-1) d
a100 = b + 99d
a1000 = b + (1000-1) d
a1000 = b + 999d
Then using the given condition, we have
(a+99d)-(b+99d) = 100
a-b = 100 —— (Eq 1)
Difference between their 1000th terms,
= (a+999d)-(b+999d)
= a-b (From eq 1)
= 100
Hence, the difference between 1000th terms of this AP is 100.
13. How many three-digit numbers are divisible by 7?
Solution: We know that the first and last three-digit numbers divisible by 7 are 105 and 994.
Therefore, we get an AP whose first term is 105, common difference is 7 and last term is 994. Let 994 is the nth term.
a = 105
d = 7
an = 994
n = ?
As we know that,
an = a + (n-1) d
994 = 105 + (n-1)7
889 = (n-1)7
127 = n-1
n = 128
Hence, there are 128 three-digit numbers which are divisible by 7.
14. How many multiplies of 4 lies between 10 and 250?
Solution: We know that the numbers divisible by 4 after 10 and before 250 are
12, 16, 20, …, 248
First term, a = 12
Common difference, d = 16-12 = 4
Let the nth term of this AP is 248.
an = 248
As we know that,
an = a + (n-1) d
248 = 12+(n-1)4
236 = (n-1)4
n-1 = 59
n = 60
There are 60 multiples of 4 between 10 and 250.
15. For what value of n, are the nth term of two APs: 63, 65, 67,…and 3, 10, 17,…equal?
Solution: For the AP: 63, 65, 67,…
First term, a = 63
Common difference, d = 65-63 = 2.
an = 63+(n-1)2
And for the AP 3, 10, 17, …
First term, a = 3
Common difference, d = 10-3 = 7.
an = 3+(n-1)7
Then by given condition we have
63+(n-1)2 = 3+(n-1)7
5(n-1) = 60
n-1 = 12
n = 13.
Therefore, 13th term of both the A.P.s are equal.
16. Determine the AP whose third term is 16 and the 7th term exceed the 5th term by 12.
Solution: Let a be the first term and d be the common difference of the AP.
a3 = a + (3-1)d
16 = a + 2d ——–(1)
a7 = a + (7-1)d
a7 = a + 6d
a5 = a + (5-1)d
a5 = a + 4d
a7 – a5 = 12
a + 6d – (a + 4d) = 12
a + 6d – a – 4d = 12
2d = 12
d = 6
Substituting the value of d in the equation (1) we get
16 = a+2×6
16 = a+12
a = 4
Therefore, A.P. will be
a, a+d, a+2d,…
4, 4+6, 4+2×6,…
4, 10, 16,…
17. Find the 20th term from the last term of the AP: 3, 8, 13, …, 253.
Solution: A.P. = 3, 8, 13,……, 253.
To find the 20th term from the last of the A.P., we will reverse the order of A.P.
253, …….13, 8, 3
First term, a = 253
Common difference, d = 3-8 = -5
n = 20
an = ?
As we know that,
an = a + (n-1) d
an = 253+(20-1)-5
an = 253 +19 x -5
an = 253 – 95
an = 158
Therefore the 20th term from the last term is 158
18. The sum of the 4th and 8th term of the AP is 24 and the sum of the 6th and 10th term is 44. Find the first three terms of the AP.
Solution: As we know that,
an = a + (n-1) d
a4 = a + (4-1) d
a4 = a + 3d
Similarly,
a8 = a + 7d
a6 = a + 5d
a10 = a + 9d
From the given condition,
(a+3d)+(a+7d) = 24
2a+10d = 24……(1) and
(a+5d)+(a+9d) = 44
2a+14d = 44……(2)
Subtracting the equation (1) form equation (2) we get
4d = 20
d = 5
Substituting the value of d in equation (2), we get
2a+10×5 = 24
2a+50 = 24
2a = -26
a = -13
a2 = a + d = -13 + 5 = -8
a3 = a + 2d = -13 + 2(5) = -3
Therefore, first three terms of the AP are given by -13, -8, -3.
19. Subba Rao started work in 1995 at an annual salary of ₹5000 and received an increment of ₹200 each year. In which year did his income reach ₹7000?
Solution: Since the increment of each year is same. Therefore, it forms an AP,
5000, 5200, 5400, ……….7000
Here, a = 5000
d = 200
an = 7000
n = ?
We know that,
an = a + (n-1)d
7000 = 5000+(n-1)200
2000 = (n-1)200
n-1 = 10
n = 11
Therefore, in 11 year his salary will be ₹7000.
20. Ramkali save ₹5 in the first week of a year and then increased her weekly savings by ₹75. If in the nth week, her weekly savings become ₹20.75, find n.
Solution: Since the increment is same, therefore it forms an AP
a = 5
d = 1.75
an = 20.75
We know that,
an = a + (n-1)d
20.75 = 5+(n-1)×1.75
15.75 = (n-1)×1.75
9 = n-1
n =10
Therefore, the required value of n is 10.
NCERT Solutions for Class 10 Maths Chapter 5 Exercise 5.2 – Arithmetic Progressions, has been designed by the NCERT to test the knowledge of the student on the topic – nth Term of an AP
NCERT Solutions for Class 10 Maths Chapter 5
- NCERT Solutions Class 10 Maths Chapter 5 Ex. 5.1 Arithmetic Progressions
- NCERT Solutions Class 10 Maths Chapter 5 Ex. 5.2 Arithmetic Progressions
- NCERT Solutions Class 10 Maths Chapter 5 Ex. 5.3 Arithmetic Progressions
- Maths – NCERT Solutions Class 10f
- NCERT Solutions Class 10
Download NCERT Solutions For Class 10 Maths Chapter 5 Exercise 5.2 – Arithmetic Progressions
