NCERT Solutions For Class 10 Maths Chapter 6 Exercise 6.2 Triangles

NCERT Solutions For Class 10 Maths Chapter 6 Exercise 6.2 Triangles

Download NCERT Solutions For Class 10 Maths Chapter 6 Exercise 6.2 Triangles. This Exercise contains 10 questions, for which detailed answers have been provided in this note. In case you are looking at studying the remaining Exercise for Class 10 for Maths NCERT solutions for other Chapters, you can click the link at the end of this Note.

Category	NCERT Solutions for Class 10
Subject	Maths
Chapter	Chapter 6
Exercise	Exercise 6.2
Chapter Name	Triangles

NCERT Solutions For Maths Chapter 6 ex 6.2 Class 10 Triangles

1. In given figure, (i) and (ii), DE||BC. Find EC in (i) and AD in (ii) 

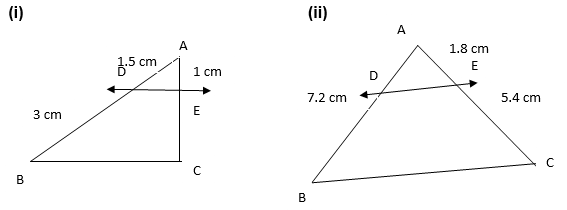
Solution:

(i) Let EC = x cm
Since DE||BC
By Basic proportionality theorem, we get


x =
x = 2
Therefore, EC = 2 cm

(ii) Let AD = x cm.
Since DE||BC in the figure (ii)
By Basic proportionality theorem, we get


x =
x = 2.4
Therefore, AD = 2.4 cm

Class 10 Maths Chapter 6 Exercise 6.2 Triangles

2. E and F are points on the sides PQ and PR respectively of a ∆ PQR. For each of the following cases state whether EF||QR:

(i) PE=3.9 cm, EQ=3 cm, PF=3.6 cm, and FR=2.4 cm
(ii) PE=4 cm, QE=4.5 cm, PF=8 cm, and RF=9 cm
(iii) PQ=1.28 cm, PR=2.56 cm, PE=0.18 cm, and PF=0.36 cm

Solution:

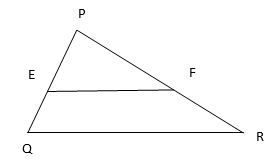
(i) Given: PE=3.9 cm, EQ=3 cm, PF=3.6 cm, and FR=2.4 cm
= 1.3
= 1.5
Since
Hence in this case EF is not parallel QR.

(ii) Given: PE=4 cm, QE=4.5 cm, PF=8 cm, and RF=9 cm


Since
Hence in this case EF is parallel to QR.

(iii) Given: PQ=1.28 cm, PR=2.56 cm, PE=0.18 cm, and PF=0.36 cm


Since
Hence in this case EF is parallel to QR.

 

3. In this figure if LM||CB and LN||CD, prove that 

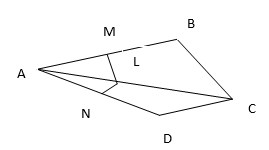
Solution: Given that LM || CB then using the basic proportionality theorem we have
……(1)
Also, LN || CD
……(2)
From equation (1) and (2) we get

Hence Proved

 

4. In the figure DE||AC and DF||AE. Prove that 

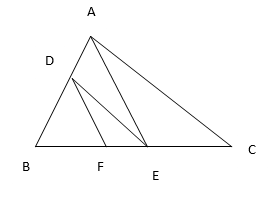
Solution: In ∆ABC we have DE||AC
Then by basic proportionality theorem, we have
….(1)
In ∆ABE we have DF||AE
Then by basic proportionality theorem, we have
……(2)
From equation (1) and (2) we get

 

5. In the figure, DE||OQ and DF||OR. Show that EF||QR.

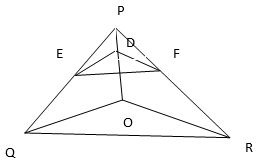
Solution: In ∆ POQ, DE||OQ
By using basic proportionality theorem, we have
……(1)
In ∆ POR, DF||OR
By using basic proportionality theorem, we have
……(2)
From equation (1) and (2) we have

By using the converse of basic property theorem, we have EF||QR.

 

6. In Figures A, B and C are the points on OP, OQ, and OR respectively such that AB||PQ and AC||PR. Show that BC||QR.

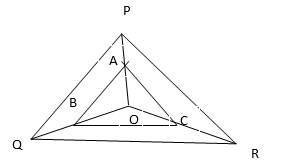
Solution: In ∆POQ, we have AB||PQ
By using the basic proportionality theorem, we have
……..(1)
In ∆POR, we have AC||PR
By using basic proportionality theorem, we have
……(2)
From equation (1) and (2), we get

By using the converse of basic proportionality theorem, we have
BC||QR

 

7. Using the basic proportionality theorem prove that the line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side. (Recall that you have proved in class IX).

Solution:

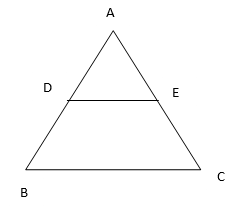
Let ∆ABC be any triangle and DE be the line drawn through the mid-point of the side AB and any point E on AC. Here DE||BC
By using the basic proportionality theorem, we have

[since D is the mid-point of AB]
AE = EC
Hence E is also the mid-point of AC.

 

8. Using the converse of basic proportionality theorem, prove that the line joining the mid-points of any sides of a triangle is parallel to the third side.

 Solution:

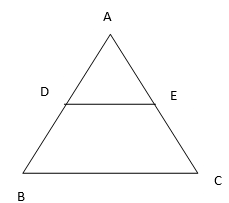
Let ∆ABC be any triangle and DE be the line segment joining mid-points D and E of the sides AB and AC respectively. Hence AD=DB and AE=EC
Therefore, and
Hence, 
By converse of basic proportionality theorem, we have DE||BC

 

9. ABCD is a trapezium in which AB||DC and its diagonal intersect each other at the point O. Show that

Solution:

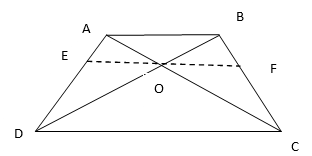
Draw a line EF passes through point O, such that EF||CD
In ∆ACD, EO||CD
By basic proportionality theorem, we have
…….(1)
In ∆ABD, EO||AB
By basic proportionality theorem, we have
…….(2)
From equation (1) and (2), we have

10. The diagonals of the quadrilateral ABCD intersect each other at the point O such that

. Show that ABCD is a trapezium.

Solution:

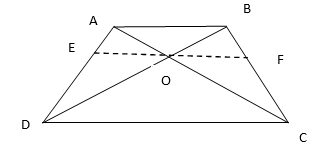
Draw a line EF parallel to AB.
In ∆ABD, EO||AB
By basic proportionality theorem, we have
……(1)
[Given]
…….(2)
From equation (1) and (2), we have

By converse of basic proportionality theorem, we have EO||DC
Hence, AB || OE || DC
⇒ AB || DC.
Therefore, ABCD is a trapezium.

NCERT Solutions for Class 10 Maths Chapter 6 Exercise 6.2 – Triangles, has been designed by the NCERT to test the knowledge of the student on the topic – Similarity of Triangles

NCERT Solutions For Class 10 Maths Chapter 6

• NCERT Solutions Class 10 Maths Chapter 6 Ex. 6.1 Triangles
• NCERT Solutions Class 10 Maths Chapter 6 Ex. 6.2 Triangles
• NCERT Solutions Class 10 Maths Chapter 6 Ex. 6.3 Triangles
• Maths – NCERT Solutions Class 10
• NCERT Solutions Class 10

Download NCERT Solutions For Class 10 Maths Chapter 6 Exercise 6.2 – Triangles