Polygons Worksheet Grade 5 contains 8 MCQ questions. Answers to Polygons Worksheet Grade 5 are available after clicking on the answer. Maths Worksheets for Class 5 help to check the concept you have learnt from detailed classroom sessions and application of your knowledge.
| Category | Maths Worksheets for Class 5 |
| Subject | Maths |
| Chapter | Polygons |
Polygons Worksheet Grade 5
Q.1) Determine, the type of Triangle for the given figure ?
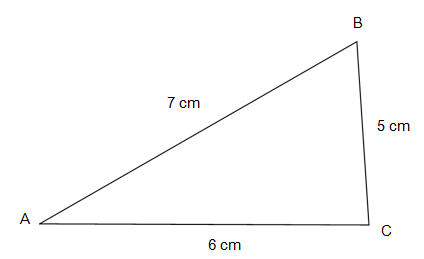
a) Equilateral Triangle
b) Isosceles Triangle
c) Scalene Triangle
Answer
Answer: c) Scalene Triangle
Explanation
In the given figure
Sides of the Triangle are
AB = 7 cm
BC = 5 cm
AC = 6 cm
We know that,
If all the sides of a Triangle are unequal, it is called a Scalene Triangle.
In the given figure all the sides of the Triangle are unequal.
Therefore, the given Triangle is a Scalene Triangle.
Q.2) Determine, the type of Triangle for the given figure ?
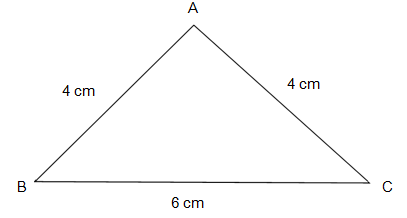
a) Equilateral Triangle
b) Isosceles Triangle
c) Scalene Triangle
Answer
Answer: b) Isosceles Triangle
Explanation
In the given figure
The Sides of the triangle are
AB = 4 cm
BC = 4 cm
AC = 6 cm
We know that,
If two of the sides of a Triangle are equal, it is called an Isosceles Triangle.
In the given figure, sides AB and BC of the Triangle are equal.
Therefore, the given Triangle is an Isosceles Triangle.
Q.3) Determine, the type of Triangle for the given figure ?
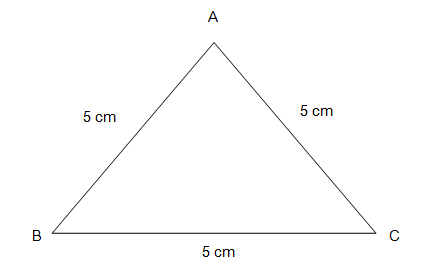
a) Equilateral Triangle
b) Isosceles Triangle
c) Scalene Triangle
Answer
Answer: a) Equilateral Triangle
Explanation
In the given figure
Sides of triangle are
AB = 5 cm
BC = 5 cm
AC = 5 cm
We know that,
If all the sides of a Triangle are equal, it is called an Equilateral Triangle.
In the given Triangle all the sides i.e. AB, BC and AC are equal.
Therefore, the given Triangle is an Equilateral Triangle.
Q.4) Determine, the type of Triangle for the given figure ?
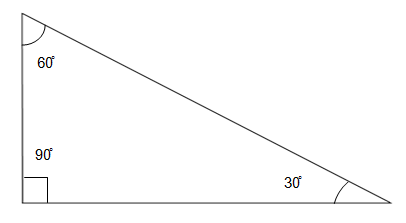
a) Acute Angled Triangle
b) Obtuse Angled Triangle
c) Right Angled Triangle
Answer
Answer: c) Right Angled Triangle
Explanation
In the given figure
The three angles of the Triangle are, 30˚, 60˚ and 90˚
We know that,
If one angle of a triangle is equal to 90˚, it is called a Right Angled Triangle.
In the given figure one of the angles in the Triangles is equal to 90˚
Therefore, the given Triangle is a Right Angled Triangle.
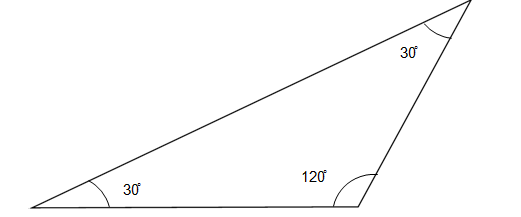
Q.5) Determine, the type of Triangle for the given figure ?
a) Obtuse Angled Triangle
b) Acute Angled Triangle
c) Right Angled Triangle
Answer
Answer: a) Obtuse Angled Triangle
Explanation
In the given figure
The three angles of the Triangle are 30˚, 30˚ and 120˚
We know that,
If one angle of a triangle is more than 90˚ (known as Obtuse angle), It is called an Obtuse Angled Triangle.
In the given figure one of the angles is 120˚, which is more than 90˚
Therefore, the given Triangle is an obtuse angled Triangle.
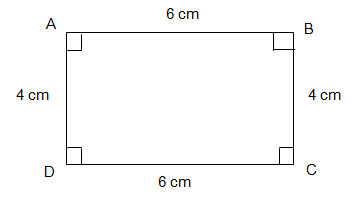
Q.6) Determine whether the given figure is a Square or Rectangle ?
a) Square
b) Rectangle
Answer
Answer: b) Rectangle
Explanation
Square – Square is a 2D shape in which all the sides are equal and each angle is of 90˚.
Rectangle – Rectangle is 2D shape is which Opposite sides are equal and each angle is 90˚.
In the given figure,
AB = CD = 6 cm and AD = BC = 4 cm and each angle is Right angle
Therefore, the given figure is a Rectangle (Since all the sides are not equal, it is not a square).
Polygons Worksheet Grade 5
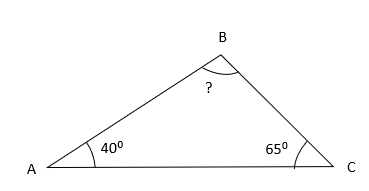
Q.7) If the two angles of the Triangle are ∠A = 40˚ , ∠C = 65˚, find ∠B ?
a) ∠B = 65˚
b) ∠B = 85˚
c) ∠B = 75˚
Answer
Answer: c) ∠B = 75˚
Explanation
In the given figure,
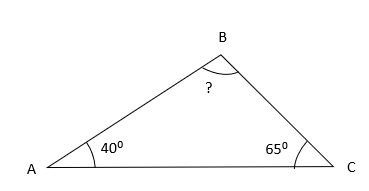
∠A = 40˚
∠C = 65˚
∠B = ?
We know that,
Sum of all the angles of Triangle = 180˚
Therefore,
∠A + ∠B + ∠C = 180˚
40˚ + 65˚ + ∠B = 180˚
105˚ + ∠B = 180˚
∠B = 180˚ – 105˚
∠B = 75˚
Q.8) In the given figure , find x˚ and y˚ ?
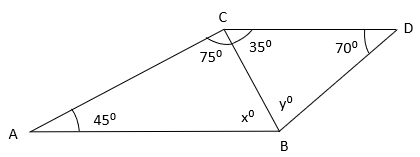
a) x˚ = 50˚ , y˚ = 85˚
b) x˚ = 70˚ , y˚ = 65˚
c) x˚ = 60˚ , y˚ = 75˚
Answer
Answer: c) x˚ = 60˚ , y˚ = 75˚
Explanation
In the given figure,
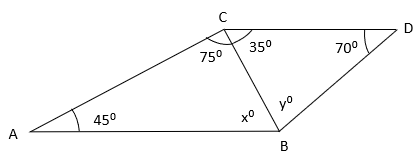
In Δ ABC
∠A = 45˚
∠ABC = x˚
∠ACB = 75˚
We know that,
Sum of all the three angles of Traingle = 180˚
∠A + ∠ABC + ∠ACB = 180˚
45˚ + x˚ + 75˚ = 180˚
120˚ + x˚ = 180˚
x˚ = 180˚ – 120˚
x˚ = 60˚
Similarly,
In Δ BCD
∠BCD = 35˚
∠CBD = y˚
∠D = 70˚
∠BCD + ∠CBD + ∠D = 180˚
35˚ + y˚ + 70˚ = 180˚
105˚ + y˚ = 180˚
y˚ = 180˚ – 105˚
y˚ = 75˚
Maths Worksheets for Grade 5
- Factors and Multiples Worksheet for Grade 5
- Fractions Worksheets Grade 5
- Ratio and Proportion Worksheets Grade 5
- Profit and Loss Worksheet for Grade 5
- Simple Interest Worksheets for Class 5
- Percentage Worksheets for Grade 5
- Perimeter Area and Volume Worksheets for Class 5
- Polygons Worksheet Grade 5
- Number Patterns Grade 5 Worksheets