Newton’s Second Law of Motion

The motion of bodies around us was associated with forces acting on them by the three laws of motion given by Isaac Newton. These three laws establish a relationship between the motion of a body with the forces that are responsible for its state of motion or compel it to change its state of motion. Newton’s second law of motion gives the dependence of force on momentum of a body.

We will now look at this law in detail but before that it is necessary to note that when two bodies of different masses, a heavy one and a light one, are acted upon by the same force for the same time, the light body attains a higher velocity or higher speed than the heavy one. But the momentum gained by both the bodies is the same. The link between fore and momentum is expresses in Newton’s second law of motion.

According to Newton’s second law of motion:

The rate of change of momentum of a body is directly proportional to the applied force, and takes place in the direction in which the force acts. The rate of change of momentum of a body can be obtained by dividing the ‘change in momentum’ by ‘time taken’ for change. So, Newton’s second law of motion can be expressed as:

Force ∝ (Change in momentum)/(time taken)

Let us suppose a body of mass  having an initial velocity . The initial momentum of this body will be  . Suppose a force  acts on this body for time  and causes the final velocity to become . The final momentum of this body will be . Now, the change in momentum of this body is  and the time taken for this change to happen is . So, according to Newton’s second law of motion:

Force ∝ (mv – mu)/(t)

Force ∝ m(v – u)/(t)

But (v-u)/t represents change in velocity with time which is known as acceleration . So, by writing  in place of (v-u)/t in the above relation, we get:

F ∝ m × a

Thus, the force acting on a body is directly proportional to the product of ‘mass’ of the body and ‘acceleration’ produced in the body by the action of the force, and it acts in the direction of acceleration. This can be used as another statement of Newton’s second law of motion.

The relation F ∝ m × a  can be turned into an equation by putting in a constant .

Thus,

F = k × m × a (where, k is constant)

The value of constant  is equal to 1 in SI units.

So, our final equation is

F = m × a

Force = mass × acceleration

Thus, Newton’s second law of motion gives us a relationship between ‘force’ and ‘acceleration’. When a force acts on a body, it produces acceleration in the body, the acceleration produced may be positive or negative.

Newton’s second law of motion also gives us a method of measuring the force in terms of mass and acceleration. the force acting on a body can be calculated by using the formula: F = m × a

We can also write the above equation as:

a = F/m

It is obvious from the above relation that: the acceleration produced in a body is directly proportional to the force acting on it and inversely proportional to the mass of the body. That is why it is easier to move lighter bodies and difficult to move heavier bodies when same amount of force is applied on them.

The SI unit of force is Newton which is denoted by N.

A newton is a force which when acting on a body of mass 1 kg produces an acceleration of 1 m/s² in it. As we know that,

F = m × a

Putting mass=1 kg and a=1 m/s², F becomes 1 newton:

So, 1 newton = 1 kg × m/s²

Now, we know that according to Newton’s first law of motion, if no force is applied on a body, its state of motion does not change. We can derive this result from Newton’s second law of motion. When no force is acting on the body, the acceleration is zero. Hence, no change can be brought in the speed of the body.

Applications of Newton’s second law of motion –

Newton’s second law of motion relates force with momentum and the observations that are explained using Newton’s second law usually focus on reducing force by altering the momentum or time taken by the body to change it.

1. A cricket player or fielder moves his hands backwards on catching a fast cricket ball. This is done to prevent injury to the hands. A fast moving cricket ball has a large momentum. In stopping the ball, its momentum reduces to zero. Now, when a cricket player moves back his hands on catching the fast ball, then the time taken to reduce the momentum of ball to zero is increased. Due to more time taken to stop the ball, the rate of change of momentum of the ball is decreased and hence, a small force is exerted on the hands of player.
2. These days all cars are provided with seat belts for passengers to prevent injuries in case of an accident. In a car accident, a fast running car stops suddenly. Due to this momentum of the car reduces to zero in a very short interval of time. The stretchable seat belts worn by passengers increase the time taken by the passengers to fall forwards. Due to the longer time, the rate of change of momentum is reduced and hence less force acts on the passenger.

Questions related to Newton’s second law of motion in NCERT textbook – Page 128 and 129

Question 5 –

A truck starts from rest and rolls down a hill with a constant acceleration. It travels a distance of 400 m in 20 s. find Its acceleration. find the force acting on it if its mass is 7 metric tonnes. (hint 1 metric tonne=1000 kg).

Solution –

Initial velocity (u) = 0

Distance travelled = 400 m

Time taken = 20 s

Acceleration (a) =?

Using, s = ut + (1/2)at²

400 = 0 × 20 + (1/2) × a ×(20)²

400  = a × 200

a = 400/200

a = 2m/s²

Force, F = ma

F = 7 × 1000 × 2

F = 14000 N

Question 6 –

A stone of 1 kg is thrown with a velocity of 20 ms^-1 across the frozen surface of a lake and comes to rest after travelling a distance of 50 m. What is the force of friction between the stone and the ice?

Solution –

Initial velocity (u) = 20 m/s

Final velocity (v) = 0

Acceleration (a) =?

Distance travelled = 50 m

Using, v² = u² + 2as

0 = (20)² + 2 × a ×50

0 = 400 + 100 a

100 a = -400

a = (-400)/100

Now, a = -4 m/s²

Force (F) = m × a

F = 1 × (-4)

F = -4N

The force of friction between ice and stone is 4 newtons.

Question 7 –

An 8000 kg engine pulls a train of 5 wagons, each of 2000 kg, along a horizontal track. If the engine exerts a force of 40000 N and the track offers a friction force of 5000 N, then calculate: (a) the net accelerating force and (b) the acceleration of the train and (c) the force of wagon 1 on wagon 2.

Solution –

Force exerted by the engine is 40000 N and the opposing force of friction is 5000 N

(a) Net accelerating force = 40000 – 5000
= 35000 N

(b) Net accelerating force = 35000 N
The mass of one wagon = 2000 kg
Mass of whole train = 5×2000 kg = 10000 kg
F = m × a
35000 = 10000 x a
a = 35000/10000
a = 3.5 m/s²

(c) force of wagon 1 on wagon 2

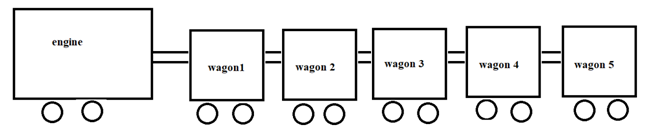
Wagon 1 has 4 wagons behind it. Total mass will be mass of 4 wagons

Force of wagon 1 on wagon 2 = mass of 4 wagons × acceleration
= 2000 × 4 × 3.5
= 28000 N

Question 8 –

 An automobile vehicle has a mass of 1500 kg. What must be the force between the vehicle and road if the vehicle is to be stopped with a negative acceleration of 1.7 m/s?

Solution –

Mass of vehicle = 1500 kg
Acceleration = -1.7 m/s²
Using, F = ma
F = 1500 × (-1.7)N
= -2550 N

Question 9 –

What is the momentum of an object of mass m, moving with a velocity v?

(a) (mv)²
(b) mv²
(c) ½ mv²
(d) mv

Solution –

(d) mv 

Conclusion – Newton’s second law of motion establishes a relationship between rate of change of momentum and force acting on a body. It also gives a relationship between acceleration and mass. The formula F=ma is useful in solving many real-life problems as shown above. This law helps to understand many observations and draw inferences about certain situations.