Download NCERT Solutions for Class 9 Maths Chapter 10 Exercise 10.4 – Circles. This Exercise contains 6 questions, for which detailed answers have been provided in this note. In case you are looking at studying the remaining Exercise for Class 9 for Maths NCERT solutions for Chapter 10 or other Chapters, you can click the link at the end of this Note.
NCERT Solutions for Class 9 Maths Chapter 10 Exercise 10.4 – Circles
NCERT Solutions for Class 9 Maths Chapter 10 Exercise 10.4 – Circles
1. Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
Solution :
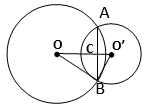
Given : Radius of the circle with center O is 5 cm
Radius of the circle with center O’ is 3 cm
OO’ = 4 cm
OB = OA = 5 cm
O’A = O’B = 3 cm
Let, OC = x cm
=> O’C = (4 – x) cm
From the triangle OCB,
(since triangle OCB is a right angled triangle)
OC2Â +Â CB2Â =Â OB2
=> x2 + CB2Â =Â 25Â Â ..(1)
From the triangle O’BC
(since the triangle is the right angled triangle)
O’C2Â +Â CB2Â =Â O’B2
=> (4 – x)2 + CB2 = 9Â ..(2)
Subtracting equation (2) from equation (1)
=> x2 – (4 – x )2Â Â =Â 16
=> x2 – 16 – x2 + 8x = 16
=> 8x = 32
=> x = 4 cm
Substituting x in equation (2)
=> (4 – 4)2 + CB2Â =Â 9
=> CB2Â =Â 9
=> CB = 3 cm
Since OC is the perpendicular bisector of AB
AC = CB
=> AC = CB = 3 cm
=> AB = AC + CB
AB = 3 + 3
=> ABÂ =Â 6 cm
Therefore, length of the chord = 6 cm
2. If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
Solution :
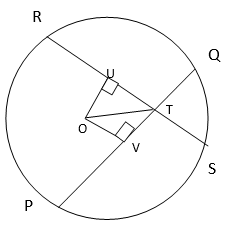
Let the two equal chords are PQ & RS
O is the center of the circle.
Construction :
Draw perpendiculars OV and OU on these chords and they also will be the bisectors of the chords.
From the triangles OVT & OUT
∠OUT = ∠OVT (Each 90˚)
OT = OT ( common side)
OV = OU (Equal chords are equidistant from the centers)
=> ∆ OVT and ∆ OUT are congruent.( RHS congruency rules)
=> VT = UT ( corresponding sides are equal in congruent triangles)Â ..(1)
Given, PQ = RS ..(2)
=> (1/2) PQ = (1/2)Â RS
=> PV = RUÂ Â ..(3)
Adding equation (1) & equation (3)
=> PV + VT =Â RU + UT
=> PTÂ =Â RTÂ ..(4)
Subtract equation (4) from equation (2)
=> PQÂ –Â PT = RSÂ –Â RT
=> QT = STÂ ..(5)
Equation (4) & Equation (5)
The segments of one chord are equal to corresponding segments of the other chord.
Hence Proved.
3. If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
Solution :
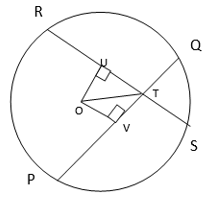
Let the two equal chords are PQ & RS
O is the center of the circle.
Construction :
Draw perpendiculars OV and OU on these chords and they also will be the bisectors of the chords.
From the triangles OVT & OUT
∠OUT = ∠OVT (Each 90˚)
OT = OT ( common side)
OV = OU (Equal chords are equidistant from the centers)
=> ∆ OVT and ∆ OUT are congruent.( By RHS congruency rules)
=> ∠OTV = ∠OTU ( corresponding angles are equal in congruent triangles)
Hence, The line joining the point of intersection to the centre makes equal angles with the chords.
4. If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D, prove that AB = CD (see Figure).
                                             Â
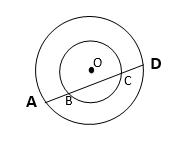
Solution :
Let us draw a perpendicular OM on line AD
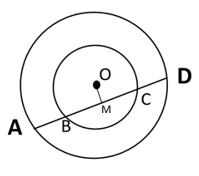
OM is the Perpendicular bisector of AD and BC
Since, AD & BC are chord of the concentric circles.
=> BMÂ =Â MC …(1)
& AMÂ =Â MDÂ …(1)
from equation (2)
AM – BM = MD – MC
=> ABÂ =Â CD
5. Three girls Reshma, Salma and Mandip are playing a game by standing on a circle of radius 5m drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If the distance between Reshma and Salma and between Salma and Mandip is 6m each, what is the distance between Reshma and Mandip?
Solution :
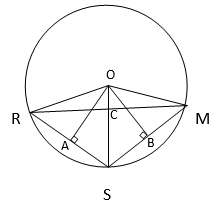
Construction :
Draw perpendiculars from O on SM and RS.
R – Reshma
S – Salma
M – Mandip
Given :
OR = OM = OS = 5 m  ( radius of the circle )
RSÂ =Â SMÂ =Â 6 m
ARÂ =Â (1/2) SM = 3 m
From the triangle OAR,
OA2Â +Â AR2Â =Â OR2
=> OA2Â + 9Â =Â 25
=> OA2 Â =Â 16
=> OAÂ Â =Â 4 m
Since OR = OM & RS = SM,
ORSM will be a kite.
And we know that in a kite,
Diagonals are perpendicular to each other and the diagonal which is common in both the isosceles triangle will bisect the other diagonal.
∠RCS = 90°  &  RC = CM
Area of the triangle ORS,
(1/2) x RC x OS =Â (1/2) x RS x OA
=> (1/2) x RC x 5Â =Â (1/2) x 6 x 4.
=> RCÂ =Â ( 24 / 5 )
=> RCÂ =Â Â 4.8 m
RMÂ =Â 2 RC
=>Â RMÂ =Â 9.6 m
=>Â Distance between Reshma and Mandip is 9.6 m
6. A circular park of radius 20m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone.
Solution :
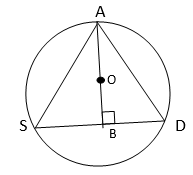
Let,
A – Ankur
SÂ Â – Syed
D – David
O is the center of the circle
OB is the perpendicular drawn on chord SD and it will also bisects the chord SD.
Given,
ASÂ =Â SDÂ =Â DA
OAÂ =Â OSÂ =Â ODÂ =Â 20 m
Since the triangle ASD is an equilateral triangle, circumcenter will coincide with its centroid.
So, O will be the centroid.
We know that centroid divides the median in 2:1 ratio .
Here AB is the perpendicular bisector of the chord SD. So, it will acts as median(through A) of the triangle ASD
(OA / OB)Â =Â (2/1)
=> (20/OB)Â =Â 2
=> OBÂ =Â 10 m
ABÂ =Â OAÂ +Â OB
=> ABÂ =Â 10 + 20
AB = 30 m
From the right angled triangle ABD,
AB2Â +Â BD2Â =Â AD2
=>Â 900 +Â (AD/2)2Â =Â AD2
=>Â AD2Â –Â (AD2/4) = 900
=>Â (3/4) AD2 = 900
=>Â AD2 = 1200
=> AD = 20√3 m
=> AS = AD = SD = 20√3 m
=> The length of the string of each phone = 20√3 m
NCERT Solutions for Class 9 Maths Chapter 10 Exercise 10.4 – Circles, has been designed by the NCERT to test the knowledge of the student on the topic – Equal Chords and Their Distances from the Centre
The next Exercise for NCERT Solutions for Class 9 Maths Chapter 10 Exercise 10.5 – Circles can be accessed by clicking here.
Download NCERT Solutions for Class 9 Maths Chapter 10 Exercise 10.4 – Circles
