Download NCERT Solutions for Class 9 Maths Chapter 10 Exercise 10.3 – Circles. This Exercise contains 3 questions, for which detailed answers have been provided in this note. In case you are looking at studying the remaining Exercise for Class 9 for Maths NCERT solutions for Chapter 10 or other Chapters, you can click the link at the end of this Note.
NCERT Solutions for Class 9 Maths Chapter 10 Exercise 10.3 – Circles



NCERT Solutions for Class 9 Maths Chapter 10 Exercise 10.3 – Circles
1. Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
Solution :
(i)
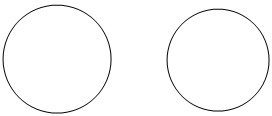
These circles doesn’t have any point in common. As they are not intersecting each other.
(ii)
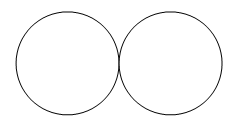
These circles have one common point. As they are touching each other externally.
(iii)
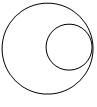
These circles have one common point. As they are touching each other internally.
(iv)
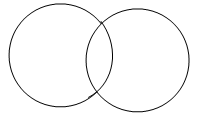
These circles have two common points. As they are intersecting each other.
(v) Consider the case when two congruent circles are taken and super impose each other, then there will be infinite points. That is, drawing the same circle two times.
2. Suppose you are given a circle. Give a construction to find its centre.
Solution :
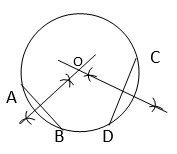
Step -1 : Take the given circle.
Step – 2 : Draw any two different chords ( AB & CD ).
Step – 3 : Draw the perpendicular bisectors of those two different chords. The intersection point of those perpendicular bisectors is the center of the circle.
Here, O is the centre of the circle.
3. If two circles intersect at two points, prove that their centres lie on the perpendicular bisector of the common chord.
Solution :
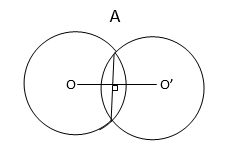
Here A and B are the intersecting points of two circles with centers O and O’.
Join AB.
Since, AB is the chord of the circle with center O, the perpendicular bisector of AB will pass through O.
Also, AB is the chord of the circle with center O’ , the perpendicular bisector of AB will pass through O’.
So, clearly the line OO’ will be the perpendicular bisector of AB ( common chord ).
=> Centers lies on the perpendicular bisector of the common chord.
Hence Proved.
NCERT Solutions for Class 9 Maths Chapter 10 Exercise 10.3 – Circles, has been designed by the NCERT to test the knowledge of the student on the following topics:-
- Perpendicular from the Centre to a Chord
- Circle through Three Points
The next Exercise for NCERT Solutions for Class 9 Maths Chapter 10 Exercise 10.4 – Circles can be accessed by clicking here.
Download NCERT Solutions for Class 9 Maths Chapter 10 Exercise 10.3 – Circles
