NCERT Solutions for Class 8 Maths Chapter 6 Exercise 6.4
NCERT Solutions for Class 8 Maths Chapter 6 Exercise 6.4 contains 6 questions and each question has explained in detail and stepwise. If you are class 8th student and currently preparing ex 6.4 class 8 maths then you must be looking for the class 8 maths chapter 6 exercise 6.4 solution for your exams preparation. Here we are providing complete class 8 maths chapter 6 exercise 6.4 solution.
Table of Content
| Category | NCERT Solutions Class 8 |
| Subject | Maths |
| Chapter | Chapter 6 |
| Exercise | Exercise 6.3 |
| Chapter Name | Square and Square Roots |
NCERT Solutions for Class 8 Maths Chapter 6 Exercise 6.1 Square and Square roots, has been designed by the NCERT to test the knowledge of the student on the following topics :
- Finding square root by division method
- Square Roots of Decimals
- Estimating Square Root
NCERT Solutions for Class 8 Maths Chapter 6 Exercise 6.4
Q.1 Find the square root of each of the following numbers by division method.
(i) 2304
(ii) 4489
(iii) 3481
(iv) 529
(v) 3249
(vi) 1369
(vii) 5776
(viii) 7921
(ix) 576
(x) 1024
(xi) 3136
(xii) 900
Solution:
(i) To calculate the square root of 2304
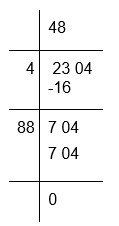
Therefore, √2304 = 48
(ii) To calculate the square root of 4489
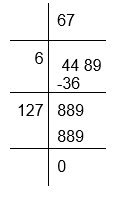
Therefore, √4489 = 67
(iii) To calculate the square root of 3481
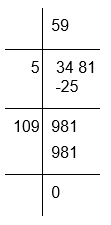
Therefore, √3481 = 59
(iv) To calculate the square root of 529
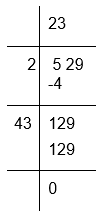
Therefore, √529 = 23
(v) To calculate the square root of 3249
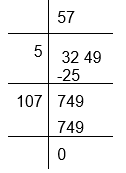
Therefore, √3249 = 57
(vi) To calculate the square root of 1369
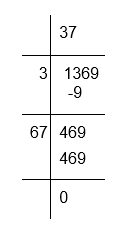
Therefore, √1369 = 37
(vii) To calculate the square root of 5776
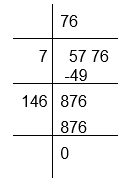
Therefore, √5776 = 76
(viii) To calculate the square root of 7921
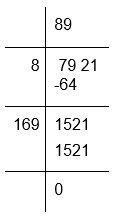
Therefore, √7921 = 89
(ix) To calculate the square root of 576
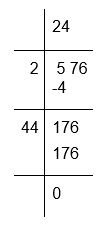
Therefore, √576 = 24
(x) To calculate the square root of 1024
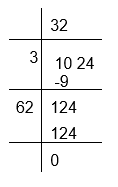
Therefore, √1024 = 32
(xi) To calculate the square root of 3136
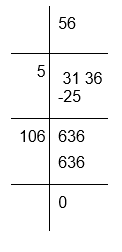
Therefore, √3136 = 56
(xii) To calculate the square root of 900
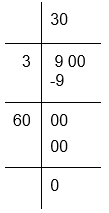
Therefore, √900 = 30
Q.2 Find the number of digits in the square root of each of the following numbers (without any calculation).
(i) 64
(ii) 144
(iii) 4489
(iv) 27225
(v) 390625
Solution:
By placing bars,
(i) We get only one bar on 64, So the square root of 64 will have only one digit
(ii) We get two bars on 144, So the square root of 144 will have two digits
(iii) We get two bars on 4489, So the square root of 4489 will have two digits
(iv) We get three bars on 27225, So the square root of 27225 will have three digits
(v) We get three bars on 390625, So the square root of 390625 will have three digits
Class 8 Maths Chapter 6 Exercise 6.4 Solution
Q.3 Find the square root of the following decimal numbers.
(i) 2.56
(ii) 7.29
(iii) 51.84
(iv) 42.25
(v) 31.36
Solution:
To calculate the square root of 2.56
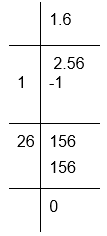
Therefore, √2.56 = 1.6
(ii) To calculate the square root of 7.29
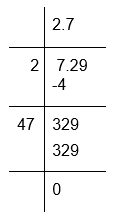
Therefore, √7.29 = 2.7
(iii) To calculate the square root of 51.84

Therefore,√51.84 = 7.2
(iv) To calculate the square root of 42.25
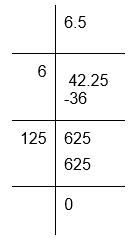
Therefore, √42.25 = 6.5
(v) To calculate the square root of 31.36
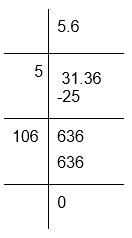
Therefore, √31.36 = 5.6
Q.4 Find the least number which must be subtracted from each of the following numbers so as to get a perfect square. Also find the square root of the perfect square so obtained.
(i) 402
(ii) 1989
(iii) 3250
(iv) 825
(v) 4000
Solution:
(i) To calculate the square root of 402
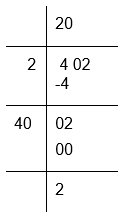
The remainder is 2
If we subtract 2 from 402 the resultant number will be 400 which is a perfect square, whose square root is 20
Therefore, required perfect square = 402 − 2 = 400
√400 = 20
(ii) To calculate the square root of 1989
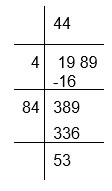
The remainder is 53
If we subtract 53 from 1989 the resultant number will be 1936 which is a perfect square, whose square root is 44
Therefore, required perfect square = 1989 − 53 = 1936
√1936 = 44
(iii) To calculate the square root of 3250
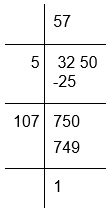
The remainder is 1
If we subtract 1 from 3250 the resultant number will be 3249 which is a perfect square, whose square root will be 57
Therefore, required perfect square = 3250 − 1 = 3249
√3249 = 57
(iv) To calculate the square root of 825
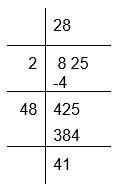
The remainder is 41
If we subtract 41 from 825 the resultant number will be 784 which is a perfect square, whose square root is 28
Therefore, required perfect square = 825 − 41 = 784
√784 = 28
(v) To calculate the square root of 4000
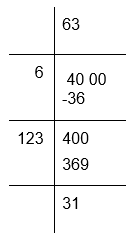
The remainder is 31
If we subtract 31 from 4000 the resultant number will be 3969 which is a perfect square whose square root is 63
Therefore, required perfect square = 4000 − 31 = 3969
√3969 = 63
Q.5 Find the least number which must be added to each of the following numbers so as to get a perfect square. Also find the square root of the perfect square so obtained.
(i) 525
(ii) 1750
(iii) 252
(iv) 1825
(v) 6412
Answer:
(i) To calculate the square root of 525
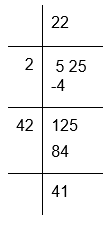
The remainder is 41.
525 is greater than square of 22 by 41. The next perfect square is 232 = 529
Hence, number to be added to 525 = 232 − 525 = 529 − 525 = 4 and √529 = 23
(ii) To calculate the square root of 1750
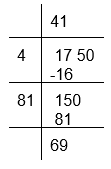
The remainder is 69.
1750 is greater than square of 41 by 69. The next perfect square is 422 = 1764
Hence, number to be added to 1750 = 422 − 1750 = 1764 − 1750 = 14 and √1764 = 42
(iii) To calculate the square root of 252
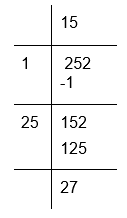
The remainder is 27
252 is greater than square of 15 by 27. The next perfect square is 162 = 256
Hence, number to be added to 252 = 162 − 252 = 256 − 252 = 4 and √256 = 16
(iv) To calculate the square root of 1825
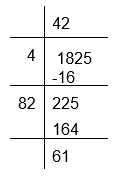
The remainder is 61
1825 is greater than square of 42 by 61. The next perfect square is 432 = 1849
Hence, number to be added to 1825 = 432 − 1825 = 1849 − 1825 = 24 and √1849 = 43
(v) To calculate the square root of 6412
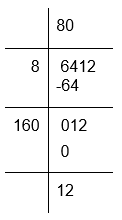
The remainder is 12
642 is greater than square of 80 by 12. The next perfect square is 812 = 6561
Hence, number to be added to 6412 = 812 − 6412 = 6561 − 6412 = 149 and √6561 = 81
Q.6 Find the length of the side of a square whose area is 441 m2.
Solution:
Let, length of each side of the square be x m.
Area of square = (x)2 = 441 m2 ( given )
x = √441
To calculate the square root of 441
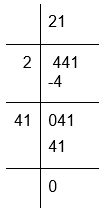
Therefore, √441 = 21
Hence, length of each side of the square is 21 m.
Q.7 In a right angled triangle ABC, ∠B = 90
(a) If AB = 6 cm, BC = 8 cm, find AC
(b) If AC = 13 cm, BC = 5 cm, find AB
Solution:
Given, ABC is right angled triangle
Applying Pythagoras theorem, we get
AC2 = AB2 + BC2
(a) AB = 6 cm, BC = 8 cm
AC2 = (6 cm)2 + (8 cm)2
AC2 = (36 + 64) cm2 =100 cm2
AC = √100 = 10 cm
AC = 10 cm
(b) AC = 13 cm, BC = 5 cm
(13 cm)2 = (AB)2 + (5 cm)2
AB2 = (13 cm)2 − (5 cm)2 = (169 − 25) cm2 = 144 cm2
AB = √144 = 12 cm
AB = 12 cm
Q.8 A gardener has 1000 plants. He wants to plant these in such a way that the number of rows and the number of columns remain same. Find the minimum number of plants he needs more for this.
Solution:
Given, A gardener has 1000 plants.
The number of rows and the number of columns should be same.
Let, the number of rows be x and number of columns be x.
To calculate square root of 1000
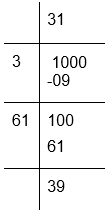
The remainder is 39
The next perfect square is 322 = 1024
Hence, to make 1000 a perfect square 322 − 1000 = 1024 − 1000 = 24 should be added
Therefore, the required number of plants is 24.
Q.9 These are 500 children in a school. For a P.T. drill they have to stand in such a manner that the number of rows is equal to number of columns. How many children would be left out in this arrangement?
Solution:
Given, there are 500 children in the school.
They have to stand for a P.T. drill in such a way that the number of rows is equal to the number of columns.
To calculate the square root of 500
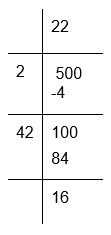
The remainder is 16.
500 is greater than square of 22 by 16.
Therefore, 16 has to be subtracted from 500 to make it a perfect square.
Therefore, the number of children who would be left out in this arrangement is 16.
NCERT Solutions for Class 8 Maths Chapter 6
- Exercise 6.1 – Square and Square roots
- Exercise 6.2 – Square and Square roots
- Exercise 6.3 – Square and Square roots
- Exercise 6.4 – Square and Square roots
The next Exercise for NCERT Solutions for Class 8 Maths Chapter 7 Exercise 7.1 Cube and Cube roots can be accessed by clicking here
Download NCERT Solutions for Class 8 Maths Chapter 6 Exercise 6.4
