NCERT Solutions for Class 8 Maths Chapter 7 Exercise 7.1
NCERT solutions for class 8 maths chapter 7 exercise 7.1contains 6 questions and each question has explained in detail and stepwise. If you are class 8th student and currently preparing class 8 maths chapter 7 exercise 7.1 maths then you must be looking for the maths class 8 chapter 7 exercise 7.1 solution for your exams preparation. Here we are providing complete ncert solutions for class 8 maths chapter 7 exercise 7.1.
Table of Content
| Category | NCERT Solutions Class 8 |
| Subject | Maths |
| Chapter | Chapter 7 |
| Exercise | Exercise 7.1 |
| Chapter Name | Cube and Cube roots |
NCERT Solutions for Class 8 Maths Chapter 7 Exercise 7.1 Cube and Cube roots, has been designed by the NCERT to test the knowledge of the student on the following topics:
- Introduction
- Cubes
Some interesting patterns
1. Adding consecutive odd numbers
2. Cubes and their prime factors
Smallest multiple that is a perfect cube
NCERT Solutions for Class 8 Maths Chapter 7 Exercise 7.1 Cube and Cube Roots
Q.1 Which of the following numbers are not perfect cubes?
(i) 216
(ii) 128
(iii) 1000
(iv) 100
(v) 46656
Solution:
(i) Prime factorisation of 216:
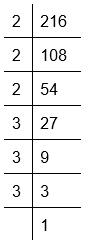
216 = 2 × 2 × 2 × 3 × 3 × 3 = 23 × 33
Here, factors of 216 can be grouped in triples.
Therefore, 216 is a perfect cube.
(ii) Prime factorisation of 128:
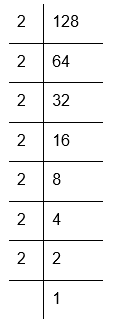
128 = 2 × 2 × 2 × 2 × 2 × 2 × 2
Here, all factors of 128 cannot be grouped in triples as one 2 is remaining.
Therefore, 128 is not a perfect cube.
(iii) Prime factorisation of 1000:

1000 = 2 × 2 × 2 × 5 × 5 × 5
Here, all factors of 1000 can be grouped in triples
Therefore, 1000 is a perfect cube.
(iv) Prime factorisation of 100:
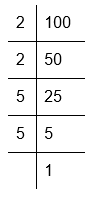
100 = 2 × 2 × 5 × 5
Here, factors of 100 cannot be grouped in triples
Therefore, 100 is not a perfect cube.
(v) Prime factorisation of 46656:

46656 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3 × 3 × 3 × 3
Here, factors of 46656 can be grouped in triples.
Therefore, 46656 is a perfect cube.
Q.2 Find the smallest number by which each of the following numbers must be multiplied to obtain a perfect cube.
(i) 243
(ii) 256
(iii) 72
(iv) 675
(v) 100
Solution:
(i) 243 = 3 × 3 × 3 × 3 × 3
Here, after grouping the factors into triples, two 3’s is left. To make them a group of triples one 3 has to be multiplied
243 × 3 = 3 × 3 × 3 × 3 × 3 × 3 = 729 is a perfect cube.
Hence, the smallest natural number by which 243 must be multiplied to make it a perfect cube is 3.
(ii) 256 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
Here, after grouping the factors into triples, two 2’s is left. To make them a group of triples one 2 has to be multiplied
256 × 2 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 512 is a perfect cube.
Hence, the smallest natural number by which 256 must be multiplied to make it a perfect cube is 2.
(iii) 72 = 2 × 2 × 2 × 3 × 3
Here, after grouping the factors into triples, two 3’s is left. To make them a group of triples one 3 has to be multiplied
72 × 3 = 2 × 2 × 2 × 3 × 3 × 3 = 216 is a perfect cube.
Hence, the smallest natural number by which 72 must be multiplied to make it a perfect cube is 3.
(iv) 675 = 3 × 3 × 3 × 5 × 5
Here, after grouping the factors into triples, two 5’s is left. To make them a group of triples one 5 has to be multiplied
675 × 5 = 3 × 3 × 3 × 5 × 5 × 5 = 3375 is a perfect cube.
Hence, the smallest natural number by which 675 must be multiplied to make it a perfect cube is 5.
(v) 100 = 2 × 2 × 5 × 5
Here, factors of 100 cannot be grouped in triples. To make them a group of triples one 2 and one 5 has to be multiplied
100 × 2 × 5 = 2 × 2 × 2 × 5 × 5 × 5 = 1000 is a perfect cube
Hence, the smallest natural number by which 100 must be multiplied to make it a perfect cube is 2 × 5 = 10.
Q.3 Find the smallest number by which each of the following numbers must be divided to obtain a perfect cube.
(i) 81
(ii) 128
(iii) 135
(iv) 192
(v) 704
Solution:
(i) 81 = 3 × 3 × 3 × 3
Here, one 3 is left after grouping factors in triples.
81 has to be divided by 3, to make it a perfect cube.
81 ÷ 3 = 27 = 3 × 3 × 3 is a perfect cube.
Hence, the smallest number by which 81 must be divided to make it a perfect cube is 3
(ii) 128 = 2 × 2 × 2 × 2 × 2 × 2 × 2
Here, one 2 is left after grouping factors in triples
128 has to be divided by 2, to make it a perfect cube.
128 ÷ 2 = 64 = 2 × 2 × 2 × 2 × 2 × 2 is a perfect cube.
Hence, the smallest number by which 128 must be divided to make it a perfect cube is 2
(iii) 135 = 3 × 3 × 3 × 5
Here, one 5 is left after grouping factors in triples
135 has to be divided by 5, to make it a perfect cube.
135 ÷ 5 = 27 = 3 × 3 × 3 is a perfect cube.
Hence, the smallest number by which 135 must be divided to make it a perfect cube is 5
(iv) 192 = 2 × 2 × 2 × 2 × 2 × 2 × 3
Here, one 3 is left after grouping the factors in triples
192 has to be divided by 3, to make it a perfect cube.
192 ÷ 3 = 64 = 2 × 2 × 2 × 2 × 2 × 2 is a perfect cube.
Hence, the smallest number by which 192 must be divided to make it a perfect cube is 3
(v) 704 = 2 × 2 × 2 × 2 × 2 × 2 × 11
Here, one 11 is left after grouping the factors in triples
704 has to be divided by 11, to make it a perfect cube
704 ÷ 11 = 64 = 2 × 2 × 2 × 2 × 2 × 2 is a perfect cube.
Hence, the smallest number by which 704 must be divided to make it a perfect cube is 11
Q.4 Parikshit makes a cuboid of plasticine of sides 5 cm, 2 cm, 5 cm. How many such cuboids will he need to form a cube?
Solution:
Given, Parikshit makes a cuboid of sides 5 cm, 2 cm, 5 cm
To form a cube with these cuboids:
LCM of 5, 2 and 5 = 10
Therefore, length of each side of cube should be 10 cm
For this arrangement, we have to put, 2 cuboids along with its length ( 2×5=10 ),
5 along with its width ( 5×2=10 ), and 2 along with its height ( 2×5=10 )
Therefore, total cuboids required = 2 × 5 × 2 = 20
NCERT Solutions for Class 8 Maths Chapter 7
The next Exercise for NCERT Solutions for Class 8 Maths Chapter 7 Exercise 7.2 Cube and Cube roots can be accessed by clicking here
