Mensuration Class 8 MCQ Questions with Answers Maths are covered in this Article. Mensuration Class 8 MCQs Test contains 31 questions. Answers to MCQs on Mensuration Class 8 Maths are available at the end of the last question. These MCQ have been made for Class 8 students to help check the concept you have learnt from detailed classroom sessions and application of your knowledge.
| Board | CBSE |
| Textbook | Maths (NCERT) |
| Class | Class 8 |
| Chapter | Chapter 11 Mensuration |
Mensuration Class 8 MCQ Questions with Answers
1.In a trapezium, the parallel sides are 4 cm and 7 cm, and the distance between them is 14 cm, find its area?
(a) 71 cm2
(b) 77 cm2
(c) 83 cm2
Answer
Answer: (b) 77 cm2
Explanation: Given:
Length of one of the parallel side = 4 cm
Length of other parallel side = 7 cm
Distance between parallel sides = 14 cm
Area of trapezium = (1/2) x ( sum of two parallel sides ) x ( distance between them )
Area of trapezium = { (1/2) x ( 4 + 7 ) x 14 } cm2
Area of trapezium = { (1/2) x ( 11 ) x 14 }cm2
Area of trapezium = (154/2)cm2
Area of trapezium = 77 cm2
2.The area of trapezium is 120 cm2 and the distance between its parallel sides is 10 cm . If the length of its one of the parallel side is 8 cm , find the length of the other parallel side?
(a) 15 cm
(b) 16 cm
(c) 14 cm
Answer
Answer: (b) 16 cm
Explanation: Given:
Area of trapezium = 120cm2
Distance between parallel sides = 10 cm
Length of one of the parallel side = 8 cm
Length of other parallel side = ?
Let the length of the other parallel side be y cm
Area of trapezium = (1/2) x ( sum of two parallel sides ) x ( distance between them )
120 cm2 = {(1/2) x ( 8 + y ) x 10 } cm2
120 = 40 + 5y
120 – 40 = 5y
5y = 80
y = 80/5
y = 16
Hence, the length of other parallel side is 16 cm
3.The area of trapezium is 60 cm2 and the distance between its parallel sides is 6 cm. If difference between the length of parallel sides is 2 cm, find the length of its parallel sides ?
(a) 10 cm and 12 cm
(b) 9 cm and 11 cm
(c) 8 cm and 10 cm
Answer
Answer: (b) 9 cm and 11 cm
Explanation: Given:
Area of trapezium = 60 cm2
Distance between parallel sides = 6 cm
Difference between the length of parallel sides = 2 cm
Let the length of one parallel side be y cm
then, the length of other parallel side be ( y + 2 ) cm
Area of trapezium = (1/2) x ( sum of two parallel sides ) x ( distance between them )
60 cm2 = { (1/2) x ( y + y + 2 ) x 6 } cm2
60 = { (1/2) x ( 2y + 2 ) x 6 }
60 = { ( 2y + 2 ) x 3
60/3 = 2y + 2
20 = 2y + 2
20 – 2 = 2y
18 = 2y
y = 18/2
y = 9
Therefore,
Length of one of its parallel side = y cm = 9 cm
Length of other parallel side = ( y + 2 ) cm = ( 9 + 2 ) cm = 11 cm
Mensuration Class 8 MCQ Questions with Answers
4.The area of trapezium is 64 cm2 and the perpendicular distance between the parallel sides is 8 cm. If the ratio of its parallel sides are 1 : 3, then find its smaller side ?
(a) 2 cm
(b) 12 cm
(c) 4 cm
Answer
Answer: (c) 4 cm
Explanation: Given:
Area of trapezium = 64 cm2
Distance between parallel sides = 8 cm
Ratio of its parallel sides = 1 : 3
Let the length of one parallel side be 1y cm
then, the length of other parallel side would be 3y cm
Area of trapezium = (1/2) x ( sum of two parallel sides ) x ( distance between them )
64 cm2 = { (1/2) x ( 1y + 3y ) x 8 } cm2
64 = { (1/2) x ( 4y ) x 8 }
64 = ( 4y x 4 )
64/(4×4) = y
y = 4
Therefore,
Length of one of its parallel side = 1y cm = ( 1 x 4 ) cm = 4 cm
Length of its other parallel side = 3y cm = ( 3 x 4 ) cm = 12 cm
Hence, the length of the smaller side is 4 cm
5.If the base and height of triangle are 12 cm and 15 cm respectively, find its area ?
(a) 90 cm2
(b) 86 cm2
(c) 82 cm2
Answer
Answer: (a) 90 cm2
Explanation: Given:
Base = 12 cm
Height = 15 cm
As we know that,
Area of triangle = (1/2) x Base x Height
Area of triangle = ( (1/2) x 12 x 15 ) cm2
Area of triangle = 90 cm2
6.The area of triangle is 24 cm2 and its base is 6 cm. Find the length of its height?
(a) 10 cm
(b) 9 cm
(c) 8 cm
Answer
Answer: (c) 8 cm
Explanation: Given:
Area of triangle = 24 cm2
Base = 6 cm
Height = ?
Let,
the height of the triangle be = y cm
As we know that,
Area of triangle = (1/2) x Base x Height
24 = (1/2) x 6 x y
(24×2)/6 = y
y = 8
Hence, the length of the height of the Triangle would be 8 cm
7.The area of triangle is 180 cm2 and its height is 15 cm. Find the length of its base ?
(a) 22 cm
(b) 23 cm
(c) 24 cm
Answer
Answer: (c) 24 cm
Explanation: Given:
Area of triangle = 180 cm2
Height = 15 cm
Base = ?
Let,
the Base of the Triangle = y cm
As we know that,
Area of triangle = (1/2) x Height x Base
180 = (1/2) x 15 x y
(180×2)/15 = y
y = 24
Hence, the length of the base of the Triangle would be 24 cm
Mensuration Class 8 MCQ Questions with Answers
8.In the given figure, ABCD is a quadrilateral in which AC = 14 cm, BE ⏊ AC, DF ⏊ AC such that BE = 12 cm and DF = 7 cm. Find the area of quadrilateral ABCD?
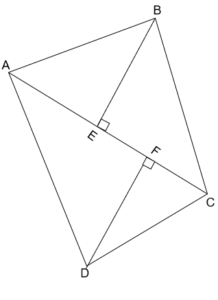
(a) 256 cm2
(b) 266 cm2
(c) 268 cm2
Answer
Answer: (b) 133 cm2
Explanation :
BE ⏊ AC
DF ⏊ AC
AC = 14 cm
BE = 12 cm
DF = 7 cm
Area of quad. ABCD = Area of ∆ABC + Area of ∆ADC
Area of ∆ABC = { (1/2) x base x height }
Area of ∆ABC = { (1/2) x AC x BE }
Area of ∆ABC = { (1/2) x 14 x 12 } cm2
Area of ∆ABC = 84 cm2
Area of ∆ADC = { (1/2) x base x height }
Area of ∆ADC = { (1/2) x AC x DF }
Area of ∆ADC = { (1/2) x 14 x 7 } cm2
Area of ∆ADC = 49 cm2
Area of quad. ABCD = Area of ∆ABC + Area of ∆ADC
Area of quad. ABCD = 84 cm2 + 49 cm2
Area of quad. ABCD = 133 cm2
9.The dimensions of a rectangular water tank are 1m 40cm by 3m 10cm by 3m 10cm . How many litres of water does it hold when filled to the brim ?
(a) 13354 Litres
(b) 13454 Litres
(c) 13054 Litres
Answer
Answer: (b) 13454 Litres
Explanation: We are given that
Length of water tank ( l ) = 1m 40cm
= (1+(40/100)m (1cm=(1/100)m)
= ( 1 + 0.4 )m
= 1.4m
Breadth of water tank ( b ) = 3m 10cm
= (3+(10/100))m (1cm=(1/100)m)
= 3 + 0.1
= 3.1m
Height of water tank ( h ) = 3m 10cm
= (3+(10/100))m (1cm=(1/100)m)
= ( 3 + 0.1 )m
= 3.1m
Capacity of water tank = Volume of water tank
Volume of water tank = l x b x h
= ( 1.4 x 3.1 x 3.1 ) m3
Now 1 m3 = 1000 Litres
So, 13.454 m3 = 13.454 x 1000 Litres of water
= 13454 Litres of water
10.The area of a courtyard is 3200 m2. Find the cost of covering it with gravel to a height of 7cm , if the gravel costs ₹ 10 per cubic metre ?
(a) ₹ 2240
(b) ₹ 2220
(c) ₹ 2280
Answer
Answer: (a) ₹ 2240
Explanation: In this question we are given
Area of courtyard = 3200 m2
Height of gravel required = 7cm
= (7/100)m (1cm=(1/100)m)
= 0.07m
Volume of gravel = Area of courtyard x Height of gravel
= 3200 x 0.07
= 224m3
Costs of 1m3 gravel = ₹ 10
Costs of 224m3 gravel = ₹ 10 x 224
= ₹ 2240
11.Find the length of the longest pole that can be put in a room of dimensions 6m by 12m by 10m ?
(a) 12.73m
(b) 14.73m
(c) 16.73m
Answer
Answer: (c) 16.73m
Explanation: Dimensions of room are given as
Length (l) = 6m
Breadth (b) = 12m
Height (h) = 10m
Longest pole that can be put in a room, Diagonal (d) =√l2+b2+h2
= √62+122+102
= √36+144+100
= √280
= 16.73m ( approx )
12.How many bricks will be required for a wall which is 12m long, 15m high and 10cm thick , if each brick measures 8cm x 10cm x 5cm ?
(a) 45200
(b) 45000
(c) 44600
Answer
Answer: (b) 45000
Explanation: Length of wall = 12m
= 12 x 100 = 1200cm
Breath of wall of wall = 10cm
Height of wall = 15m
= 15 x 100 = 1500cm
Volume of wall = L x B x H
= ( 1200 x 10 x 1500 ) cm3
Volume of 1 brick = l x b x h
Dimensions of brick
l = 8cm
b = 10cm
h = 5cm
Volume = ( 8 x 10 x 5 ) cm3
Number of brick required = Volume of wall
Volume of 1 brick
= (1200×10×1500)/8×10×5
= 45000
So, the Number of brick required to build the wall = 45000
13.How many persons can be accommodated in a hall of length 12m , breadth 15m and height 10m , assuming that 4m3of air is required for each persons ?
(a) 410 persons
(b) 450 persons
(c) 440 persons
Answer
Answer: (b) 450 persons
Explanation: To find the number of persons that can be accommodated in a hall
We have to find the Volume of hall
Dimensions of hall are given as under
Length of hall ( l ) = 12m
Breadth of hall ( b ) = 15m
Height of hall ( h ) = 10m
Volume of hall = l x b x h
= ( 12 x 15 x 10 ) m3
= 1800m3
Volume of air required by each persons = 4m3
Number of persons that can be accommodated in a hall = Volume of hall / Volume required by each person
= 1800/4
= 450
So, the Number of persons that can be accommodated in a hall = 450 persons
14.Find the Lateral surface area and Total surface area of Cuboid which is 18m long , 12m wide and 4.5m high ?
(a) Lateral surface area of a Cuboid = 330m2 , Total surface area of a Cuboid = 722m2
(b) Lateral surface area of a Cuboid = 270m2 , Total surface area of a Cuboid = 702m2
(c) Lateral surface area of a Cuboid = 230m2 , Total surface area of a Cuboid = 670m2
Answer
Answer: (b) Lateral surface area of a Cuboid = 270m2 , Total surface area of a Cuboid = 702m2
Explanation: We are given that,
Length of Cuboid ( l ) = 18m
Breadth of Cuboid ( b ) = 12m
Height of Cuboid ( h ) = 4.5m
Lateral surface area of a Cuboid = 2 ( l + b ) x h
= 2 ( 18 + 12 ) x 4.5
= 2 x 30 x 4.5
Lateral surface area of a Cuboid = 270 m2
Total surface area of a Cuboid = 2 ( l b + b h + h l )
= 2 ( 18 x 12 + 12 x 4.5 + 4.5 x 18 )
= 2 ( 216 + 54 + 81 )
= 2 x 351
Total surface area of a Cuboid = 702 m2
Mensuration Class 8 MCQ Questions with Answers
15.The volume of a reservoir is 300 m3 . Water is poured into into it at the rate of 50 litres per minute . How many hours will it take to fill the reservoir ?
(a) 80 hours
(b) 105 hours
(c) 100 hours
Answer
Answer: (c) 100 hours
Explanation: Volume of reservoir = 300m3
= 300 x 1000 ( 1 m3 = 1000 litres )
= 300000 litres
Rate of flow of water = 50 litres per minute
Time taken to fill the reservoir =Volume of reservoir in litres/Rate of flow of water in litres per minute
=(300000/50)min
= 6000 min
=(6000/60)hours ( 1 min = 1/60 hours )
= 100 hours
16.Find the volume of a Cuboid which is 8m long , 5m wide and 5.5m high ?
(a) 240 m3
(b) 220 m3
(c) 190 m3
Answer
Answer: (b) 220 m3
Explanation: We are given that,
Length of Cuboid ( l ) = 8m
Breadth of Cuboid ( b ) = 5m
Height of Cuboid ( h ) = 5.5m
Volume of Cuboid is l x b x h
Therefore,
Volume of Cuboid = ( 8 x 5 x 5.5 ) m3
= 220 m3
17.Find the volume of the wood used to make a closed rectangular box of outer dimensions 12cm x 20cm x 15cm , if the thickness of wood is 4.5cm all around ? Also, find the capacity of the box ?
(a) 3202 cm3
(b) 3402 cm3
(c) 2902 cm3
Answer
Answer: (b) 3402 cm3
Explanation: External length = 12cm
External breadth = 20cm
External height = 15cm
Thickness = 4.5cm
Therefore,
Internal length = ( External length – 2 x Thickness )
= ( 12 – 2 x 4.5 )
= ( 12 – 9 ) cm
= 3cm
Internal breadth = ( External breadth – 2 x Thickness )
= ( 20 – 2 x 4.5 )
= ( 20 – 9 ) cm
= 11cm
Internal height = ( External height – 2 x Thickness )
= ( 15 – 2 x 4.5 )
= ( 15 – 9 ) cm
= 6cm
Now,
Volume of the wood required to make the box = External volume – Internal volume
= ( External length x External breadth x External height ) – ( Internal length x Internal breadth x Internal height )
= ( 12 x 20 x 15 ) – ( 3 x 11 x 6 )
= 3600 – 198
= 3402cm3
18.A swimming pool is 200m long and 180m wide . If 144000 cm3 of water is pumped into it, find the height of water level in the pool ?
(a) 4m
(b) 7m
(c) 6m
Answer
Answer: (a) 4m
Explanation: Length of the swimming pool = 200m
Breadth of the swimming pool = 180m
Volume of water pumped into it = 144000 m3
Volume of water = length x breadth x height
144000 = 200 x 180 x h
h x 200 x 180 = 144000
h =144000/(200×180)
= 144000/36000
= 4m
Hence, the height of water level in swimming pool is = 4m
19.Find the Curved surface area and Total surface area of a cylinder of radius 7cm and height 25cm ?
(a) Curved surface area of cylinder = 772 cm 2 , Total surface area of cylinder = 1390 cm 2
(b) Curved surface area of cylinder = 7900 cm 2 , Total surface area of cylinder = 1430 cm 2
(c) Curved surface area of cylinder = 7700 cm 2 , Total surface area of cylinder = 1408 cm 2
Answer
Answer: (c) Curved surface area of cylinder = 7700 cm 2 , Total surface area of cylinder = 1408 cm 2
Explanation: We are given that,
Height of cylinder ( h ) = 25cm
Radius of cylinder ( r ) = 7cm
Curved surface area of cylinder = (2πrh)sq units
=(2×(22/7)×7×7×25)cm2
Curved surface area of cylinder = 7700 cm2
Total surface area of cylinder = 2πr(h+r)sq units
= 2×(22/7)×7(7+25)
= 2×(22/7)×7×32
Total surface area of cylinder = 1408 cm2
20.A cylindrical tank has a capacity of 7436 m3 and the diameter of its base is 26m . Find the depth of the tank ?
(a) 12 m
(b) 22 m
(c) 14 m
Answer
Answer: (c) 14 m
Explanation: We are given that,
Capacity of cylindrical tank = 7436 m3
Diameter of its base = 26m
Radius = 12 x Diameter
= 12 x 26 m
= 13m
Let the Depth (height) of cylindrical tank be h m
Capacity of cylindrical tank = Volume of cylindrical tank
Since,
Volume of cylindrical tank =πr2h cubic units
7436 = ( (22/7) x 13 x 13 x h )
(22/7) x 13 x 13 x h = 7436
On cross multiplication,
h = (7436×7)/22×13×13
h = 52052/3718
h = 14m
Hence, Depth of cylindrical tank = 14m
21.Find the ratio of the Curved surface area and Total surface area of a cylinder whose radius and height are 10cm and 15cm respectively ?
(a) 5 : 2
(b) 3 : 2
(c) 2 : 4
Answer
Answer: (b) 3 : 2
Explanation: We are given that,
Radius of cylinder = 10cm
Height of cylinder = 15cm
As we know the formulas
Curved surface area of cylinder = 2πrh sq units
Total surface area of cylinder = 2πr(h+r)sq units
We have to find the ratio of Curved surface area and Total surface area
So,
Curved surface area of cylinder : Total surface area of cylinder
2πrh : 2πr(h+r)
2πr From both the sides will be cancelled out
h : ( h + r )
15 : 10
3 : 2
Hence, The ratio of Curved surface area and Total surface area = 3 : 2
Mensuration Class 8 MCQ Questions with Answers
22.Find the volume of a cylinder of radius 6m and height 4.9m ?
(a) 554.4 m3
(b) 564.4 m3
(c) 534.4 m3
Answer
Answer: (a) 554.4 m3
Explanation: We are given that,
Height of cylinder = 4.9m
Radius of cylinder = 6m
Volume of cylinder is πr2h cubic units
Therefore,
Volume of cylinder = ((22/7)×6×6×4.9)m3
= 554.4 m3
Hence, the Volume of cylinder = 554.4 m3
23.If the Total surface area of a cuboid is 456 cm2 and the ratio of the edges of cuboid are 1 : 3 : 4 , find the volume of cuboid ?
(a) 20706 cm3
(b) 20776 cm3
(c) 20736 cm3
Answer
Answer: (c) 20736 cm3
Explanation: We are given that,
Total surface area of cuboid = 456 cm2
Ratio of edges of cuboid = 1 : 3 : 4
Let the sides of cuboid be 1x , 3x and 4x
Total surface area of cuboid = 2( lb + bh + hL )
456 = 2x( 1x x 3x + 3x x 4x + 4x x 1x )
456 = 2 x ( 3x + 12x + 4x )
456 = 2 x 19x
38x = 456
x = 456/38
= 12
Edges of cuboid = 1x
= 1 x 12 = 12cm
= 3x
= 3 x 12 = 36cm
= 4x
= 4 x 12 = 48cm
Volume of cuboid = l x b x h
= 12 x 36 x 48
= 20736 cm3
24.If a rectangular shape paper of 10cm width is rolled along its width to form a cylinder of radius 14cm . Find the volume of the cylinder ?
(a) 6660 cm3
(b) 6160 cm3
(c) 6060 cm3
Answer
Answer: (b) 6160 cm3
Explanation: Since, the rectangular shape of paper is rolled along its width
Therefore, the height of the cylinder so formed would be 10cm
So,
Height of cylinder = 10cm
Radius of cylinder = 14cm
We know that,
Volume of cylinder = πr2h cubic units
=((22/7)×14×14×10)cm3
= 6160 cm3
Hence, the Volume of cylinder is = 6160 cm3
25.If the Curved surface area of a cylinder is 121 m2 and its height is 14m , find the Volume of the cylinder ?
(a) 22296 m3
(b) 21296 m3
(c) 21096 m3
Answer
Answer: (b) 21296 m3
Explanation: Curved surface area of a cylinder = 121 m2
Height of a cylinder (h) = 14m
We know that,
Curved surface area of a cylinder = (2πrh) sq units
121 = (2πrh) sq units
121 = 2 x (22/7) x r x 14
2 x (22/7) x r x 14 = 121
r = (121×7)/2×22×14
r = (5.5×7)/2×14
= (5.5×1)/2×2
r = 5.5/4
Volume of a cylinder = πr2h cubic units
= ((22/7)×(5.5/4)×(5.5/4)×14 ) m3
Volume of cylinder = 21296 m3
26.If the length , width and height of an iron beam are 10m , 20cm and 30cm respectively, and if 1 cubic metre of iron weighs 30 kg , what is the weight of the beam ?
(a) 18 kg
(b) 30kg
(c) 13 kg
Answer
Answer: (a) 18 kg
Explanation : We are given that,
Length of iron beam = 10m
Width of iron beam = 20cm
= 20/100 m ( 1cm = 1/100 m )
Height of iron beam = 30cm
= 30/100 m ( 1cm = 1/100 m )
Volume of iron beam = Length x Width x Height
= 10 x (20/100) x (30/100) m3
if 1 cubic metre of iron weighs = 30 kg
Weight of iron beam = 10 x (20/100) x (30/100) x 30 kg
= 180000/10000
= 18 kg
27.A solid rectangular piece of iron measures 14m x 10cm x 5cm . Find the weight of this piece in Kilograms if 1cm3 of iron weighs 10 grams ?
(a) 692 kg
(b) 704 kg
(c) 700 kg
Answer
Answer: (c) 700 kg
Explanation: Length of rectangular piece of iron ( l ) = 14m
= 14 x 100 cm ( 1m = 100cm )
= 1400cm
Breadth of rectangular piece of iron ( b ) = 10cm
Height of rectangular piece of iron ( h ) = 5cm
Volume of rectangular piece of iron = l x b x h
= ( 1400 x 10 x 5 ) cm3
We need to find the weight of of rectangular piece of iron = 70000 cm3
Weight of 1 cm3 of iron = 10 grams
Weight of 70000cm3 of iron = 10 x 70000
= 700000
= 700000 grams
= 700000/1000 Kg (1gm=1/1000Kg)
= 700 Kg
28.A field is 30m long and 70m broad . In one corner of the field , a pit which is 20m long , 5 m broad and 10m deep has been dug out . The earth taken out of it is evenly spread over the remaining part of the field . Find the rise in the level of the field ?
(a) 200 cm
(b) 50 cm
(c) 100 cm
Answer
Answer: (b) 50 cm
Explanation: Area of the field = length of the field x breadth of the field
Area of the field = 30 x 70
= 2100 m2
Are of the pit = length of pit x breadth of pit
= 20 x 5
= 100 m2
Area over which the earth is spread out = ( Area of the field – Are of the pit )
= ( 2100 – 100 ) m2
= 2000 m2
Volume of earth dug out will be equal to the volume of = length of pit x breadth of pit x depth of pit
= 20 x 5 x 10
= 1000 m3
Rise in the level of the field = Volume of earth dug out
Area over which the earth is spread out
= 1000/2000
= 0.5m
= 0.5 x 100 cm ( 1m = 100cm )
= 50cm
Hence, the rise in the level of the field = 50cm
Mensuration Class 8 MCQ Questions with Answers
29.If the circumference of the circular base of a cylinder is 440cm and its height is 4cm , find the volume of the cylinder ?
(a) 61600 m3
(b) 61630 m3
(c) 61300 m3
Answer
Answer: (a) 61600 m3
Explanation: We are given that,
Circumference of circular base of cylinder = 440cm
Height of cylinder = 4cm
Circumference of circle = 2πr
440 = 2πr
2 x (22/7) x r = 440
r = (440/44) x 7
r = 70cm
Volume of cylinder = πr2h cubic units
= ( (22/7) x 70 x 70 x 4 ) cm3
Volume of cylinder = 61600cm3
30.If the ratio of radii of two cylinders is 4 : 3 , and the ratio their heights is 5 : 8 , find the ratio of their volumes ?
(a) 10 : 6
(b) 8 : 10
(c) 10 : 9
Answer
Answer: (c) 10 : 9
Explanation: We are given that,
Ratio of radii of two cylinders = 4 : 3
Ratio of heights of two cylinders = 5 : 8
Let the radii of two cylinders be 4r and 3r
And heights of two cylinders be 5h and 8h
Volume of cylinder = πr2h cubic units
Therefore, the ratio of Volume of two cylinders
π x 4r x 4r x 5h : π x 3r x 3r x 8h
π will be cancelled out from both the sides
4r x 4r x 5h : 3r x 3r x 8h
80rh : 72rh
10 : 9
Hence, the ratio of Volume of two cylinders = 10 : 9
31.The external radius of an iron pipe is 7cm and the thickness of the pipe is 3cm . If the pipe is 21cm long and iron weighs 10 g/cm3, find the weight of the pipe ?
(a) 21.78 kg
(b) 23.78 kg
(c) 20.78 kg
Answer
Answer: (a) 21.78 kg
Explanation: We are given that,
External radius of iron pipe = 7cm
Thickness of the pipe = 3cm
Length of the pipe = 21cm
Internal radius = ( External radius – Thickness of the pipe )
= ( 7 – 3 ) cm
= 4cm
External volume of the pipe = πR2H cubic units
= ( (22/7) x 7 x 7 x 21 ) cm3
= 3234 cm3
Internal volume of the pipe = πr2hcubicunits
= ( (22/7) x 4 x 4 x 21 ) cm3
= 1056 cm3
Volume of iron = External volume of the pipe – Internal volume of the pipe
= ( 3234 – 1056 ) cm3
= 2178 cm3
Weight of iron = 10 g/cm3
Weight of the pipe = 10 x 2178 g
= 21780 g
Or,
Weight of the pipe = 21780/1000 kg ( 1 g = 1/1000 kg )
= 21.78 kg
MCQ Questions for Class 8 Maths with Answers
- Linear Equations in One Variable Class 8 MCQ Questions
- Understanding Quadrilaterals Class 8 MCQ Questions
- Data handling Class 8 MCQ Questions with Answers
- Square and Square Roots Class 8 MCQ with Answers
- Cube and Cube Roots Class 8 MCQ Questions
- Comparing Quantities Class 8 MCQ Questions
- Exponents and Powers Class 8 MCQ
- Direct and Inverse Proportion Class 8 MCQ Questions
- Factorization Class 8 MCQ Questions
- Introduction to graphs Class 8 MCQ Questions
- Playing with Numbers Class 8 MCQ Questions
- Time and Work Class 8 MCQ Questions
Frequently Asked Questions on Mensuration Class 8 MCQ Questions
1. Are these MCQs on Mensuration Class 8 are based on 2021-22 CBSE Syllabus?
Yes. There are 31 MCQ’s on this Chapter in this blog.
2. Are you giving all the chapters of Maths Class 8 MCQs with Answers which are given in CBSE syllabus for 2021-22 ?
Yes, we are providing all the chapters of Maths Class 8 MCQs with Answers.