Triangles Class 10 MCQ with Answers – Maths Class 10 MCQ Online Test are covered in this Article. Triangles Class 10 MCQ Test contains 25 questions. Answers to MCQ on Triangles Class 10 are available after clicking on the answer. MCQ Questions for Class 10 with Answers have been made for Class 10 students to help check the concept you have learnt from detailed classroom sessions and application of your knowledge.
| Board | CBSE |
| Textbook | Maths (NCERT) |
| Class | Class 10 |
| Chapter | Chapter 6 Triangles |
| Category | MCQ Questions for Class 10 Maths with Answers |
Triangles Class 10 MCQ with Answers
1. All similar figures are congruent.
(a) True
(b) False
Answer
Answer: (b) False
Explanation: All congruent figures are similar but the similar figures need not be congruent.
2. Two polygons of the same number of sides are similar, if
(a) their corresponding angles are equal
(b) their corresponding sides are equal
(c) their corresponding sides are proportional
(d) Both A and C
Answer
Answer: (d) Both A and C
3. In a triangle ABC in which a line parallel to side BC intersects other two sides AB and AC at D and E respectively, then AB and AC are
(a) AD/DB = AE/EC
(b) AD/DB ≠ AE/EC
(c) AD/DB > AE/EC
(d) AD/DB < AE/EC
Answer
Answer: (a) AD/DB = AE/EC
Explanation:
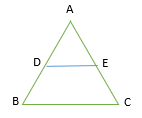
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
4. Given in a ∆ABC, AD/DB = AE/EC and ∠ADE= ∠ACB, then
(a) ∆ABC is equilateral triangle
(b) ∆ABC is isosceles triangle
(c) ∆ABC is scalene triangle
(d) Can’t say
Answer
Answer: (b) ∆ABC is isosceles triangle
Explanation:
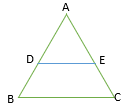
as given, AD/DB=AE/EC
So, DE || BC(If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side)
Then, ∠ADE= ∠ABC (Corresponding angles)
Given, ∠ADE= ∠ACB
By this,
∠ABC = ∠ACB
AB = AC (Sides opposite to the equal angles)
So, it is an isosceles triangle.
5. S and T are respectively the midpoints on the sides PQ and PR of a triangle PQR and QR = 7 cm. If ST || QR, then the length of ST is
(a) 3.5cm
(b) 3cm
(c) 4cm
(d) 7cm
Answer
Answer: (a) 3.5cm
Explanation: By midpoint theorem, which states that “the line segment in a triangle joining the midpoint of two sides of the triangle is said to be parallel to its third side and is also half of the length of the third side.”
ST= QR/2 = 3.5cm
6. Areas of two similar triangles are 30 cm2 and 120 cm2. If the length of a side of the larger triangle is 40 cm, then the length of the corresponding side of the smaller triangle is:
(a) 12cm
(b) 13cm
(c) 14cm
(d) 15cm
Answer
Answer: (a) 12cm
Explanation: Let the side of smaller triangle be x cm.
ar(Larger Triangle)/ar(Smaller Triangle) = (side of larger triangle/side of smaller triangle)2
120/30 = (40/x)2
x = √400
X = 20 cm
7. If in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio (or proportion) and hence the two triangles are similar. This refers to
(a) ASA criteria
(b) SAS criteria
(c) AAA criteria
(d) SSS criteria
Answer
Answer: (c) AAA criteria
8. In an ∆ DEF, GH || EF and divides the triangle in two equal areas. Find the ratio of corresponding sides.
(a) 2cm
(b) √2 cm
(c) 4cm
(d) 3cm
Answer
Answer: (b) √2 cm
Explanation:
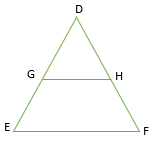
In ∆ DEF and ∆ DGH,
GH || EF
∠DEF = ∠DGH, ∠DFE = ∠DHG (Corresponding angles)
∆ DEF ~ ∆ DGH (AA Similarity)
Given, ar∆ DEF/ ar ∆ DGH = 2/1
ar∆ DEF/ ar ∆ DGH = (DE / DG)² {The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.}
(DE / DG)2 = 2/1
DE / DG = √2 /1
Triangles Class 10 MCQ with Answers
9.If in two triangles, sides of one triangle are proportional to (i.e., in the same ratio of) the sides of the other triangle, then their corresponding angles are equal and hence the two triangles are similar. This refers to
(a) ASA criteria
(b) SAS criteria
(c) AAA criteria
(d) SSS criteria
Answer
Answer: (d) SSS criteria
10.If one angle of a triangle is equal to one angle of the other triangle and the sides including these angles are proportional, then the two triangles are similar. This refers to
(a) ASA criteria
(b) SAS criteria
(c) AAA criteria
(d) SSS criteria
Answer
Answer: (b) SAS criteria
11. Which is not a right triangle.
(a) 3,4,5 (cm)
(b) 6,8,10 (cm)
(c) 4,3,7 (cm)
(d) 34,30,16 (cm)
Answer
Answer: (c) 4,3,7 (cm)
Explanation: 72 ≠ 42 + 32
12. In triangle ABC, if AB = 4 cm, AC = 12 cm, BD = 3 cm, and AD is the bisector of angle BAC, find DC
(a) 2
(b) 4
(c) 6
(d) 9
Answer
Answer: (d) 9
Explanation:
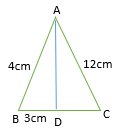
As Given, AD is the angle bisector of angle BAC,
So, by angle bisector theorem,
BD/DC = AB/AC
⇒ 3/DC = 4/12
⇒ DC = (3 X 12)/4 cm = 9 cm
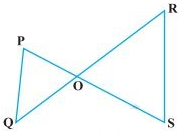
13.If PQ || RS then, ∆ POQ ~ ∆ SOR by
(a) SAS
(b) SSS
(c) AAA
(d) ASA
Answer
Answer: (c) AAA
Explanation: In ∆ POQ and ∆ SOR,
∠P=∠S (Alternate Interior angle, PQ || RS)
∠Q=∠R (Alternate Interior angle, PQ || RS)
∠POQ=∠SOR (VOA)
By AAA,
∆ POQ ~ ∆ SOR
14. All the isosceles triangles are
(a) Not Similar
(b) Congruent
(c) Both
(d) None
Answer
Answer: (a) Not Similar
15.If ∆ABC ~ ∆DEF, <A=36˚ and ∠E= 64˚, find ∠C
(a) 36˚
(b) 64˚
(c) 80˚
(d) 126˚
Answer
Answer: (c) 80˚
Explanation: given, ∆ABC ~ ∆DEF
So, ∠E= ∠B= 64˚
In ∆ABC,
∠A=36˚, ∠B= 64˚, ∠C= ?
∠A + ∠B + ∠C = 180˚
36˚ + 64˚ + ∠C = 180˚
∠C = 180˚ – 100˚ = 80˚
16.In a ∆ABC, AC = √25cm, AB = 3cm, BC = 4cm, find ∠B
(a) 30˚
(b) 60˚
(c) 90˚
(d) 120˚
Answer
Answer: (c) 90˚
Explanation: AC2 =AB2 + BC2
(√25)2 = (3)2 + (4)2
25=25
Satisfying Pythagoras, ∠B = 90˚
Triangles Class 10 MCQ with Answers
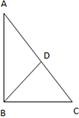
17.∆ABC is a right-angled triangle, right angled at B and BD ⊥ AC. If BD = 3cm, AB = 5 cm and BC = 5 cm find AC?
(a) 5 cm
(b) 8 cm
(c) 9 cm
(d) 10 cm
Answer
Answer: (b) 8 cm
Explanation: BD = 3cm and AB = 5cm
Now, in ∆ADB
AB2 = AD2 + BD2
AD2 = AB2 – BD2
AD2 = 25 – 9
AD2 = 16
AD = 4cm
Now, in ∆ABD and ∆CBD
BD = BD (Common Side)
∠ADB = ∠CDB (Both 90°)
AB = BC (Given)
∆ABD ≅ ∆CDB (RHS Congruency)
Therefore, AD = DC
AC = AD + DC = 2AD = 2 × 4cm = 8cm
18.The lengths of diagonals of a rhombus are 8 cm and 6 cm. What will be the length of the sides of rhombus?
(a) 6 cm
(b) 5 cm
(c) 7 cm
(d) 3 cm
Answer
Answer: (b) 5 cm
Explanation:
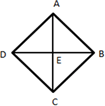
Diagonals of a rhombus bisect each other at right angles
Therefore, AE = 4cm and DE = 3cm; ∠E= 90˚
Now, in ∆AED
AD2 = AE2 + DE2
AD2 = 16 + 9
AD2 = 25
AD = √25 cm = 5 cm
19. What will be the length of the side of the rhombus inscribed in a circle of radius 3 cm?
(a) √18 cm
(b) 2√3 cm
(c) 6 cm
(d) 3√6 cm
Answer
Answer: (a) √18 cm
Explanation:
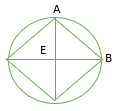
In ∆AEB,
AE= BE= 3cm (radius of the circle)
AB= ?
AB2 = AE2 + BE2 (Diagonals of the rhombus bisect each other and perpendicular)
= 9 + 9
= 18
AB = √18 cm
20.In ΔABC, if DE || BC, AD = x, DB = x + 4, AE = x – 4 and EC = x – 1, then value of x is
(a) 4
(b) 7
(c) 10
(d) 16
Answer
Answer: (d) 16
Explanation: ∆ABC ~ ∆ADE, (by AAA criteria) as DE || BC
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
Therefore,
AD/DB =AE/ EC
X/ x+4 = x-4 / x-1
X(x-1) = (x+4) (x-4)
X2 – x = x2 – 16
X = 16
21.An equilateral triangle ABC is of side 8cm. AD bisects the ∠BAC , find BD:DC.
(a) 8:4
(b) 3:2
(c) 1:1
(d) 2:3
Answer
Answer: (c) 1:1
Explanation: The Angle-Bisector theorem states that if a ray bisects an angle of a triangle, then it divides the opposite side into segments that are proportional to the other two sides.
BD / DC = AB / AC = 1:1
22.In below Figure –
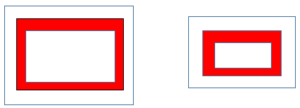
(a) All congruent figure are not Similar nor congruent.
(b) All congruent figure are not Similar but congruent.
(c) All congruent figure are Similar may or may not congruent.
(d) None of the above..
Answer
Answer: (c) All congruent figure are Similar may or may not congruent.
23.Two polygons of the same number of sides are similar, if their corresponding angles are………and their corresponding sides are ………………..
(a) Unequal, Proportional
(b) Equal, disproportional
(c) Equal; proportional
(d) Unequal, disproportional.
Answer
Answer: (c) Equal; proportional
24.Basic Proportionality Theorem Also known as ……………..
(a) Thales Theorem
(b) Mid-Point Theorem
(c) Pythagoras Theorem
(d) None of Above
Answer
Answer: (a) Thales Theorem
25. A Boy of height 180 cm is walking away from the base of a Flag at a speed of 0.8 m/s. If the Flag is 3.6 m above the ground, find the length of his shadow after 10 seconds.
(a) 4.4m
(b) 8.0m
(c) 2.4m
(d) 1.4 m
Answer
Answer: (b) 8.0m
Explanation:
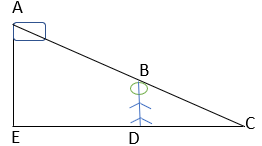
Let AE- FLAG, BD- BOY; DC- SHADOW
∠AEC = ∠BDC = 90°
∠ACE = ∠BCD
Hence ∆ACE ~ ∆BCD
So, AE / BD = EC / DC
ED = Distance travelled by boy = speed X time = .8 X10 m =8m
EC / DC = AE / BD
{ED+DC} / DC = AE / BD
{8+DC} / DC = 3.6 / 1.8
8 +DC = 2DC
DC= 8m
MCQ Questions for Class 10 Maths
- Real Numbers Class 10 MCQ with Answers
- Polynomials Class 10 MCQ with Answers
- Pair of Linear Equations in Two Variables
- MCQ Questions on Quadratic Equations for Class 10
- Arithmetic Progressions
- Triangles Class 10 MCQ with Answers
- Coordinate Geometry
- Introduction to Trignometry
- Some Applications of Trigonometry Class 10 MCQ with Answers
- Circles Class 10 MCQ with Answers
- Constructions Class 10 MCQ with Answers
- Areas Related to Circles
- Surface Areas and Volumes
- Statistics Class 10 MCQ with Answers
- Probability Class 10 MCQ
Frequently Asked Questions on Triangles Class 10 MCQ with Answers
1. Are these MCQ on Triangles Class 10 are based on 2021-22 CBSE Syllabus?
Yes . There are 25 MCQ’s on this Chapter in this blog.
2. Are you giving all the chapters of Maths Class 10 MCQs with Answers which are given in CBSE syllabus for 2021-22 ?
Yes, we are providing all the chapters of Maths Class 10 MCQs with Answers.