What is Supplementary Angles?
Two angles are said to be supplementary if the sum of their measure is 180o
Supplementary Angles Examples
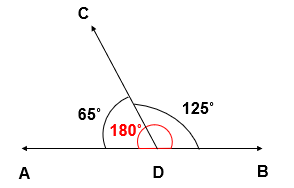
- In this figure, two angles i.e, 65˚ and 125˚ are Supplementary Angles.
As, 65˚ + 125˚ = 180˚
- In this figure, two angles i.e, 70˚ and 110˚ are Supplementary Angles.
As, 70˚ + 110˚ = 180˚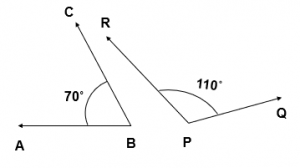
Supplementary Angles Examples
Examples 1
If two Angles are Supplementary, and one of the Angles is 65˚ , what is the measure of the other Angle?
Explanation
If two Angles are Supplementary, then their sum of measures is 180˚
Measure of one Angle = 65˚
Let the Measure of the Second Angle be = x˚
Sum of Supplementary Angles = 180˚
In other words, 65˚ + x˚ = 180˚
x˚ = 180˚ – 65˚
x˚ = 115˚
Hence, the measure of the other Angle is = 115˚
Examples 2
The difference of the measure of two supplementary Angles is 10˚ . Find the measure of Angles.
Explanation
If two Angles are supplementary, then their sum of measure is 180˚
Let the measure of one Angle = ( x )˚
Then, the measure of other Angle = ( x – 10 )˚
Sum of Supplementary Angles = 180˚
x˚ + x˚ – 10˚ = 180˚
2x˚ = 180˚ + 10˚
2x˚ = 190˚
x = 190/2
x = 95
Hence, the measure of one Angle = ( x )˚ = 95˚
and other Angle = ( x – 10 )˚ = ( 95 – 10)˚ = 85˚
Examples 3
Two supplementary Angles are in the ratio of 1 : 4 , find the Angles?
Explanation
If two Angles are Supplementary, then their sum of measure is 180˚
Let the measures of two Angles be ( 1a )˚ and ( 4a )˚
Sum of Supplementary Angles = 180˚
( 1a )˚ + (4a )˚ = 180˚
( 5a )˚ = 180˚
a = 180/5
a = 36
Hence, measure of two Angles are:
( 1a )˚ = ( 1 x 36 )˚ = 36˚
( 4a )˚ = ( 4 x 36 )˚ = 144˚