Standard form of Rational Number | Maths

Standard Form of Rational Number

Standard form of Rational Number – A Rational number a/b is said to be in Standard form if:-

• “a” and “b” are integers having no common divisor other than 1.
• “b” is a positive integer.

Examples : – 

Question 1

What is the standard form of Rational Number  24/32  ?

Explanation

Step 1: – To reduce a fraction into its standard form, we will first find the HCF of both Numerator and Denominator.

Step 2: – Thereafter, we will divide both Numerator and Denominator by their HCF

The HCF of 24 and 32 is 8

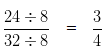
Hence, the standard form of Rational Number 24/32 is 3/4

Question 2

What is the standard form of 28/49 ?

Explanation

Step 1 : – To reduce a fraction into its standard form, we will first find the HCF of both Numerator and Denominator.

Step 2 : – Thereafter, we will divide both Numerator and Denominator by their HCF

The HCF of 28 and 49 is 7

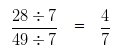
Hence, the standard form of  Rational Number 28/49 is 4/7.

Question 3

What is the standard form of Rational Number 39/(-78) ?

Explanation

Given Number = 39/(-78)

In order to reduce the given number into its standard form, we would first need to make the Denominator positive

Multiplying both the Numerator and Denominator (to make the Denominator positive) by (-1)

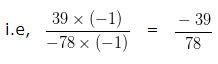
The HCF of 39 and 78 is 39

Dividing both the Numerator and Denominator by their HCF i.e, 39 we would get

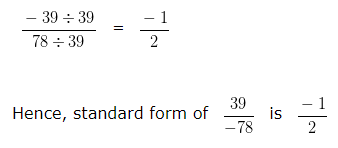
Question 4

What is the standard form of 27/(-15) ?

Explanation

Given Number = 27/(-15)

In order to reduce the given number into its standard form, we would first need to make the Denominator positive

Multiplying both the Numerator and Denominator (to make the Denominator positive) by (-1)

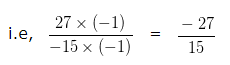
The HCF of 27 and 15 is 3

Dividing both the Numerator and Denominator by their HCF i.e, 3 we would get

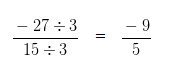
Hence, standard form of 27/(-15) is (-9)/5

Question 5

What is the standard form of 26/(-117)  ?

Explanation

Given Number = 26/(-117)

In order to reduce the given number into its standard form, we would first need to make the Denominator positive

Multiplying both the Numerator and Denominator (to make the Denominator positive) by (-1)

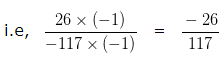
The HCF of 26 and 117 is 13

Dividing both the Numerator and Denominator by their HCF i.e, 13 we would get

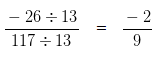
Hence, standard form of 26/(-117) is (-2)/9