Some Applications of Trigonometry Class 10 MCQ with Answers – Maths Class 10 MCQ Online Test are covered in this Article. Some Applications of Trigonometry Class 10 MCQ Test contains 20 questions. Answers to MCQs on Some Applications of Trigonometry Class 10 MCQ with Answers Maths are available at the end of the last question. These MCQ have been made for Class 10 students to help check the concept you have learnt from detailed classroom sessions and application of your knowledge.
| Board | CBSE |
| Textbook | Maths (NCERT) |
| Class | Class 10 |
| Chapter | Chapter 9 Some Applications of Trigonometry |
| Category | MCQ Questions for Class 10 Maths with Answers |
Some Applications of Trigonometry Class 10 MCQ with Answers – Maths Class 10 MCQ Online Test
1. Name a surveying instrument which is based on principles of Trigonometry.
(a) Telescope
(b) Theodolite
(c) Microscope
(d) None of the above
Answer
Answer: (b) Theodolite
2. A boy is looking on a top of a tower. Name the angle so formed by the line of sight with ground.
(a) Angle of elevation
(b) Angle of depression
(c) Angle of reflection
(d) None of the above
Answer
Answer: (a) Angle of elevation
Explanation: The angle formed by the line of sight with the horizontal when it is above the horizontal level is known as angle of elevation.
3. If a pole of height 10m casts a shadow of 10√3, then sun’s elevation.
(a) 30Ëš
(b) 45Ëš
(c) 60Ëš
(d) 90Ëš
Answer
Answer: (a) 30Ëš
Explanation:
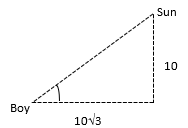
tanθ = 10/(10√3) = 1/(√3)
tanθ= tan30˚
θ= 30˚
4. A vertical tower of height H stands on a horizontal plane with 45Ëš angle of elevation. A boy of height h is standing over the tower with 60Ëš angle of elevation at horizontal plane. Find the ratio of height of tower to height of a boy.
(a) (√3+1)/(√3-1)
(b) 1/(√3+1)
(c) (√3+1)/2
(d) 2/(√3+1)
Answer
Answer: (c) (√3+1)/2
Explanation:
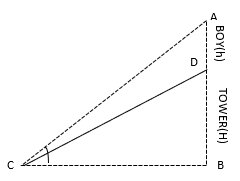
In ∆DBC ,
tan45Ëš = H/BC
BC = H…………(i)
In ∆ABC,
tan60Ëš = (H+h)/BC
BC = (H+h)/(√3) ………..(ii)
H = (H+h)/(√3)
√3 H = H + h
(√3 -1)H= h
H/h = 1/(√3 -1)
H/h = 1/(√3 -1) x (√3 +1)/(√3 +1)
= (√3 +1)/(3 -1)
= (√3 +1)/(2 )
5. A vertical tower of height H stands on a horizontal plane with 45Ëš angle of elevation. A boy of height h is standing over the tower with its 30Ëš angle of elevation from the point D which is H m vertically above the point C. Find the ratio of height of tower to height of a boy.
(a) 1:2
(b) 1: √3
(c) 2:1
(d) √3 :1
Answer
Answer: (d) √3 :1
Explanation:
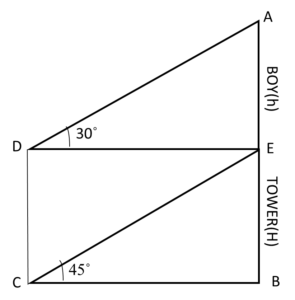
In ∆EBC,
Tan45Ëš = H/BC
BC = H……………………….(i)
In ∆AED,
Tan30Ëš = h/DE
1/√3 = h/DE
DE = √3h……………………….(ii)
BC = DE
H = √3h
H/h = (√3)/1
6. A girl of height 6m is standing on a level ground. The length of shadow changes with change in Sun’s altitude from 60˚ to 30˚. Find the change in length of her shadow.
(a) 4/√3m
(b) 4√3m
(c) √3m
(d) 12m
Answer
Answer: (b) 4√3m
Explanation:
In ∆ABC,
Tan60Ëš = AB/BC = 6/BC
√3= 6/BC
BC = 6/(√3)m
In ∆ABD,
Tan30Ëš = AB/BD = 6/BD
1/√3 = 6/BD
BD = 6√3m
Change in length of shadow = CD = BD – BC
= 6√3 – 6/(√3)
= (18 – 6)/(√3)
= 12/(√3)
= 12/(√3) x (√3)/(√3) = 4√3 m
7. Find the angle of elevation of the top of a tower of height 40m from a point on the ground, which is 40m away from the foot of the tower.
(a) 30Ëš
(b) 45Ëš
(c) 60Ëš
(d) 90Ëš
Answer
Answer: (b) 45Ëš
Explanation: tanθ = 40/40 = 1 = tan45˚
θ = 45˚
Some Applications of Trigonometry Class 10 MCQ with Answers – Maths Class 10 MCQ Online Test
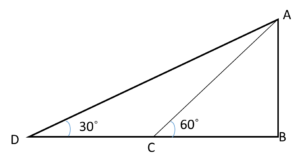
8. In below Fig. Two boys of different heights are standing facing to each other at a distance of 6m between them. The angle of elevation of the top of the two boys are 30Ëš and 60Ëš respectively. Find the heights of the boys.
(a) 6m, 3m
(b) 6√3m , 3m
(c) 6√3m, 2√3m
(d) 6m, 2√3m
Answer
Answer: (c) 6√3m, 2√3m
Explanation: Let height of boy 1 is h m and height of boy 2 is H m.
For boy 2,
Tan60Ëš = H/6
√3 = H/6
H = 6√3 m
For boy 1,
Tan30Ëš = h/6
1/√3 =h/6
h = 6/(√3)
h = 6/(√3) x (√3)/(√3) = 2√3m
9. If α and β are the angles of elevation of top of the tower vertical on a horizontal plane. The angles changes in relation to sun’s altitude. If the difference in shadow is 9m, then find the length of tower .
(a) (9 tanα tanβ)/(tanβ-tanα)
(b) 9/(tanβ-tanα)
(c) (tanα tanβ)/(tanβ-tanα)
(d) (9 tanα tanβ)/(tanβ+tanα)
Answer
Answer: (a) (9 tanα tanβ)/(tanβ-tanα)
Explanation:
In ∆ABC,
Tanβ = AB/BC
AB = BC × tanβ
BC = AB/tanβ
In ∆ABD,
Tanα = AB/BD
AB = BD × tanα
BD = AB/tanα
Change in length of shadow = CD = BD – BC
9 = AB/tanα – AB/tanβ
9 =AB ( 1/tanα – 1/tanβ )
9 tanα tanβ = AB(tanβ – tanα)
AB= (9 tanα tanβ)/(tanβ – tanα)
10. The angle of elevation of the top of a tower from two points at a distance of 16m and 25m from the base of the tower are complimentary. Find the height of the tower.
(a) 15 m
(b) 17m
(c) 20 m
(d) 22 m
Answer
Answer: (c) 20 m
Explanation: tan θ = height/16……(i)
tan (90˚- θ) = height/25 [ Angles are complementary]
1/tanθ =height/25………(ii) [ ∴ tan (90˚- θ) = cot θ = 1/tanθ ]
Multiplying (i) and (ii),
tanθ x (1/tanθ) = (height/16) x (height/25)
( height)2 = 16 x 25
Height = 20 m
11. The angle formed by the line of sight when we lower our head to see the object is
(a) Angle of elevation
(b) Angle of depression
(c) Angle of reflection
(d) None of the above
Answer
Answer: (b) Angle of depression
Explanation: The angle formed by the line of sight with the horizontal when it is below the horizontal level is known as angle of depression.
12. The angle of elevation of sun decreases with………….in length of shadow of any object.
(a) Increase
(b) Decrease
(c) No change
(d) None of the above
Answer
Answer: (a) Increase
13. Find the angle of elevation , when the length of the shadow is same as of height of the building.
(a) 30Ëš
(b) 45Ëš
(c) 60Ëš
(d) 90Ëš
Answer
Answer: (b) 45Ëš
Explanation: tanθ = height/(length of the shadow) = x/x = 1 = tan45˚
θ = 45˚
14. The angle of depression of a boy standing on the ground from top of the tower of height 60m is 60Ëš. Find the distance of the boy from tower.
(a) 60√3 m
(b) 30/ √3 m
(c) 20/ √3m
(d) 20√3m
Answer
Answer: (d) 20√3m
Explanation:
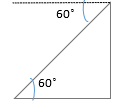
tan60Ëš= 60/x
x = 60/(√3) x (√3)/(√3) = 20√3 m
Some Applications of Trigonometry Class 10 MCQ with Answers – Maths Class 10 MCQ Online Test
15. Two poles are of equal height are standing on the ground opposite to each other as shown in given figure. Find the height of pole.
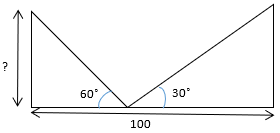
(a) 20√3m
(b) 10√3m
(c) 25√3m
(d) 25m
Answer
Answer: (c) 25√3m
Explanation: In ∆ABC,
Tan60Ëš= h/x
√3 =h/x
h = x√3 ……….(i)
In ∆EDC,
Tan30Ëš = h/(100-x)
1/(√3) = h/(100-x)
h = (100-x)/(√3)……….(ii)
From (i) and (ii)
x√3 = (100-x)/(√3)
3x = 100 – x
4x = 100
X = 25m
h = x√3 = 25√3m
16. Find the sun’s elevation, when a lamppost of 6√3m casts a shadow of 6m.
(a) 30Ëš
(b) 45Ëš
(c) 60Ëš
(d) 90Ëš
Answer
Answer: (c) 60Ëš
Explanation: tanθ = (6√3)/6 = √3 = tan60˚
θ = 60˚
17. Find the length of ladder placed against the wall of height 12m. The angle of elevation of the ladder is 30Ëš.
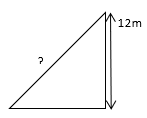
(a) 10m
(b) 24m
(c) 30m
(d) 36m
Answer
Answer: (b) 24m
Explanation: sin30Ëš = 12/x
1/2 = 12/x
x = 24m
18. At some time of the day, a boy’s shadow makes an angle of 45˚ with the ground. Find the ratio of height and length of his shadow.
(a) 1:2
(b) 2:1
(c) 1:1
(d) 1:√3
Answer
Answer: (c) 1:1
Explanation: tan45Ëš = h/l
1 = h/l
h = l
h:l = 1:1
19. The ratio of the height to length of the shadow of lamppost standing on a horizontal plane is 3:√ Find its angle of elevation.
(a) 30Ëš
(b) 45Ëš
(c) 90Ëš
(d) 60Ëš
Answer
Answer: (d) 60Ëš
Explanation: tanθ = 3/(√3) =(√3 x √3)/(√3)
= √3= tan60°
θ = 60˚
20. A tree is bend down from the mid due to storm and touches the ground making an angle of 30Ëš. The distance between the top of tree to the foot of tree is 6m. Find the length of tree.
(a) 4√3m
(b) 2√3 m
(c) √3m
(d) 3m
Answer
Answer: (a) 4√3m
Explanation: In ∆ABC,
Tan30Ëš= AB/6
1/(√3) = AB/6
AB= 6/(√3)
AB= 6/(√3) x (√3)/(√3)
AB = 2√3 m = AC [ Tree is broken from mid]
Length of tree = AB + AC
= 2√3 + 2√3
= 4√3m
MCQ Questions for Class 10 Maths
- Real Numbers Class 10 MCQ with Answers
- Polynomials Class 10 MCQ with Answers
- Pair of Linear Equations in Two Variables
- MCQ Questions on Quadratic Equations for Class 10
- Arithmetic Progressions
- Triangles Class 10 MCQ with Answers
- Coordinate Geometry
- Introduction to Trignometry
- Some Applications of Trigonometry Class 10 MCQ with Answers
- Circles Class 10 MCQ with Answers
- Constructions Class 10 MCQ with Answers
- Areas Related to Circles
- Surface Areas and Volumes
- Statistics Class 10 MCQ with Answers
- Probability Class 10 MCQ