Ratio and Proportion Problems and Solutions for Class 7

Ratio and Proportion Problems and Solutions for Class 7, deals with various concepts which are as under:-

• Convert Ratio into its simplest form
• Ratio of two quantities, by converting them into same units
• Equivalent ratios
• Find the numbers when their ratio and sum are given
• Divide sum of money between two persons when ratio are given
• Comparison of ratios
• Are the given ratio in proportion
• Are the given number are in proportion
• Find the value of y when four numbers are in proportion
• Finding Ratio A : B : C
• Finding Ratio A : B : C if Ratio A : B and B : C given
• Converting Ratio into another Ratio
• Finding ratio of present ages
• Finding ratio of ages of persons after some years
• Finding ratio of ages of persons some year ago.
• Third proportional value
• Mean proportional value
• Continued proportion

Ratio and Proportion Problems and Solutions for Class 7 – Convert Ratio into its simplest form

In order to convert the given ratio to Simplest Form, we should follow the following steps : –

• Find the HCF of both the numerator and denominator
• Dividing Both numbers by their HCF

The result is the ratio in its simplest form.

Question 1 :

Convert the ratio 66 : 18 in its simplest form

Solution:

HCF of 66 and 18 is 6

Since, 66 : 18

= 11 : 3

Hence, the simplest form of 66 : 18 is 11 : 3

Ratio and Proportion Problems and Solutions for Class 7 – Ratio of two quantities, by converting them into same units

Question 2 :

Find the ratio of 48 min to 4 hours

Solution:

Taking both the quantities in same unit, we have

4 hours = ( 4 x 60 ) = 240 min

The equation now becomes 48 min : 240 min

or

Hence, the required ratio is 1 : 5

 

Ratio and Proportion Problems and Solutions for Class 7 – Equivalent ratios

In order to find Equivalent Ratios of any given ratio, we multiply or divide the numerator and denominator of the ratio by the same non zero number.

Question 3 :

Find the Equivalent ratio of 6 : 7 ?

Solution:

On multiplying or dividing each term of a ratio by the same non zero number, we get a ratio equivalent to the given ratio

For, 24/28

Both numerator and denominator of given fraction is multiplied by same non zero number i.e 4

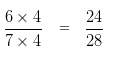
24/28 is an equivalent ratio of 6/7

7/6 is not an equivalent ratio of 6/7. As both 6 and 7 are not mutiply by

same non zero number

25/21 is not an equivalent ratio of 6/7. As both 6 and 7 are not mutiply

by same non zero number

22/21 is not an equivalent ratio of 6/7. As both 6 and 7 are not mutiply

by same non zero number

Ratio and Proportion Problems and Solutions for Class 7 – Find the numbers when their ratio and sum are given

Question 4 :

Two numbers are in the ratio 5 : 7 and their sum is 120. Find the numbers?

Solution:

Let the required number be 5a and 7a

Since the sum of these two numbers is given, we can say that

5a + 7a = 120

12a = 120

a = 120/12

a = 10

So, the first number is 5a = 5 x 10

= 50

Second number is 7a = 7 x 10

= 70

Hence, two numbers are 50 and 70

 

Ratio and Proportion Problems and Solutions for Class 7 – Divide sum of money between two persons when ratio are given

Question 5 :

Divide ₹ 2000 between X and Y in the ratio 5 : 3

Solution:

Total money = ₹ 2000

Given ratio = 5 : 3

Sum of ratio terms = ( 5 + 3 )

= 8

Give: 5/8 part of ₹ 2000 to X

Give: 3/8 part of ₹ 2000 to Y

that is,

X ‘s share = ₹ ( 2000 x 5/8) = ₹ 1250

Y ‘s share = ₹ ( 2000 x 3/8) = ₹ 750

 

Ratio and Proportion Problems and Solutions for Class 7 – Divide sum of money among three persons when ratio are given

Question 6 :

Divide ₹ 5000 among X , Y and Z in the ratio 1 : 2 : 7

Solution:

Total money = ₹ 5000

Given ratio = 1 : 2 : 7

Sum of ratio terms = ( 1 + 2 + 7 )

= 10

Share of X = ₹ ( 5000 x 1/10) = ₹ 500

Share of Y = ₹ ( 5000 x 2/10) = ₹ 1000

Share of Z = ₹ ( 5000 x 7/10) = ₹ 3500

Ratio and Proportion Problems and Solutions for Class 7 – Comparison of ratios

To Compare two Ratios, we should follow the following steps : –

• Write both the Ratios as Fractions
• Convert both the Fractions into Like Fraction:-
  – Find the L.C.M of denominator of both the Fractions
  – Make the denominator of each fraction equal to their L.C.M.
• In case of Like fractions, the number whose numerator is greater is larger.

Question 7 :

Compare the ratios ( 3 : 4 ) and ( 4 : 3 )

Solution:

We can write

( 3 : 4 ) = 3/4 and ( 4 : 3 ) = 4/3

Now, let us compare 3/4 and 4/3

LCM of 4 and 3 is 12

Making the denominator of each fraction equal to 12

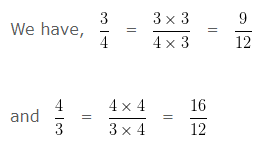
In case of Like fractions, the number whose numerator is greater is larger. Hence we can say 9/12 < 16/12

That is, 3/4 < 4/3

Hence, ( 3 : 4 ) < ( 4 : 3 )

 

Ratio and Proportion Examples With Answers – Proportion

When Two Ratios are equal then we say that they are in Proportion and use the symbol “: :” or “=” to equate two ratios.

Four Numbers in Proportion

Let a, b, c, d are four numbers said to be in proportion.
then, a : b = c : d  or a : b :: c : d
here a and d are called the extreme terms or extremes.
b and c are called the middle terms or means.
When Four numbers are in proportion
then, Product of extremes = Product of means.
i.e, In proportion a : b :: c : d,
(a x d) = (b x c)

Ratio and Proportion Problems and Solutions for Class 7 – Are the given ratio in proportion

Question 8 :

Are the ratios 15 m : 45 m and 30 km : 90 km in proportion?

Solution:

We have 15 m : 45 m

= 15 : 45

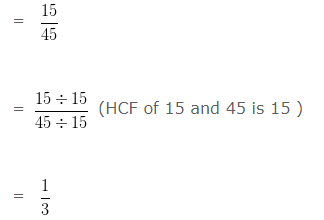
30 km : 90 km

= 30 : 90

Since, the ratios 15 m : 45 m and 30 km : 90 km are equal to 1/3. So, they are in proportion.

 

Ratio and Proportion Problems and Solutions for Class 7 – Are the given number are in proportion

Question 9 :

Are 3, 6, 5, 15 in proportion?

Solution:

Product of means = Product of extremes

Here, Means are 6 and 5

Extremes are 3 and 15

Product of extremes = 3 x 15 = 45

Product of means = 6 x 5 = 30

Since, Product of extremes ≠ Product of means

Hence, 3 , 6 , 5 , 15 are not in Proportion

Ratio and Proportion Problems and Solutions for Class 7 – Find the value of y when four numbers are in proportion

Question 10 :

If 20 : 12 : : y : 6, find the value of y?

Solution:

We know that, Product of means = Product of extremes

In the given numbers, we can say that 12 , y are means and 20 , 6 are extremes

12 x y = 20 x 6

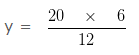
y = 10

Hence, y = 10

Question 11 :

If 45 : y : : y : 5, find the value of y?

Solution:

Clearly, Product of means = Product of extremes

y x y = 45 x 5

y² = 45 x 5

y² = 225

Hence, y = 15

 

Ratio and Proportion Problems and Solutions for Class 7 – Finding Ratio A : B : C

Question 12 :

If 3A = 5B = 4C , find A : B : C?

Solution:

Let,

3A = 5B = 4C = k

This implies that 3A = k

A = k/3

Also if 5B = k

B = k/5

Further, if 4C = k

C = k/4

A : B : C = k/3 : k/5 : k/4

LCM of 3 , 5 , 4 is 60

Multiplying each of the ratio by 60/k we get the ratios as

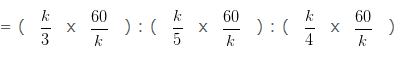
= 20 : 12 : 15

Hence, A : B : C = 20 : 12 : 15

 

Ratio and Proportion Problems and Solutions for Class 7 – Finding Ratio A : B : C if Ratio A : B and B : C given

Question 13 :

If A : B = 4 : 9 and B : C = 12 : 2, find A : B : C

Solution:

Given A : B = 4 : 9

and B : C = 12 : 2

To find A : B : C we have to make the value of common term in both the ratios equal

that is, B = 9

For this B : C = 1 : 2/12 ( On dividing each term by 12 )

B : C = ( 9 : 2/12 x 9 ) (On multiplying each term by 9 )

B : C = 9 : 18/12

We get, B : C = 9 : 3/2

Since, A = B = 4 : 9 and B : C = 9 : 3/2

Therefore, A : B : C = 4 : 9 : 3/2

Hence, A : B : C = 8 : 18 : 3 (Multiplying each term by 2 )

 

Ratio and Proportion Problems and Solutions for Class 7 – Converting Ratio into another Ratio

Question 14 :

What must be added to each term of the ratio 7 : 9 so that the new ratio becomes 7 : 8 ?

Solution:

Let the required number to be added be ‘ a ‘

then, ( 7 + a ) : ( 9 + a ) = 7 : 8

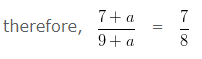
8 ( 7 + a ) = 7 ( 9 + a )

56 + 8a = 63 + 7a

8a – 7a = 63 – 56

1a = 7

Hence, the required number is 7

 

Ratio and Proportion Problems and Solutions for Class 7 – Finding ratio of present ages

Question 15 :

Present age of Sanjay is 52 years and the age of his Daughter is 28 years. Find the ratio of present age of Daughter to the present age of Sanjay ?

Solution:

Present age of Sanjay = 52 years

Present age of Daughter = 28 years

To find the ratio of present age of Daughter to the present age of Sanjay

Hence, the ratio of the present age of Daughter to Sanjay is 7 : 13

Ratio and Proportion Problems and Solutions for Class 7 – Finding ratio of ages of persons after some years

Question 16 :

Present age of Seema is 22 years and the age of her Brother is 26 years. Find the ratio of Seema’s age to her Brother’s age after 10 years.

Solution:

Present age of Seema = 22 years

After 10 years Seema’s age = 22 + 10 = 32 years

Present age of Brother = 26 years

After 10 years Brother’s age = 26 + 10 = 36 years

Ratio of age of Seema and Brother after 10 years

Taking, HCF of 32 and 36 is 4

Hence, the ratio of Seema’s age to her Brother’s age after 10 years is 8 : 9

 

Ratio and Proportion Problems and Solutions for Class 7 – Finding ratio of ages of persons some year ago.

Question 17 :

Present age of Ritu is 23 years and the age of her Brother is 18 years. What was the ratio of Ritu’s age to her Brother’s age 3 years ago?

Solution:

Present age of Ritu = 23 years

Ritu’s age 3 years ago = 23 – 3 = 20 years

Present age of Brother = 18 years

Brother’s age 3 years ago = 18 – 3 = 15 years

Ratio of age of Ritu and Brother 3 years ago

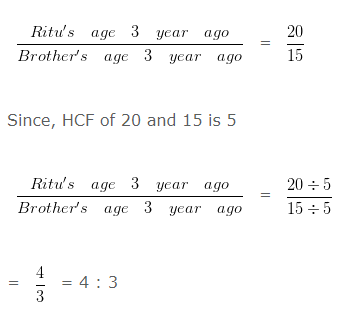
Hence, the ratio of Ritu’s age to Brother’s age is 4 : 3

 

Ratio and Proportion Problems and Solutions for Class 7 – Third proportional value

Let say a and b be two numbers and c is in third proportion with a and b

Then,

a : b = b : c

Question 18 :

Find the third proportion to 6 and 12?

Solution:

Let, the third proportion to 6 and 12 be a

6 : 12 :: 12 : a

(Product of Extremes= Product of Means)

Here, Extremes are= 6 and a

Means are = 12 and 12

6 x a = 12 x 12

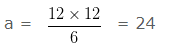
Hence, the value of ‘a’ is 24

 

Ratio and Proportion Problems and Solutions for Class 7 – Mean proportional value

Let say a and b be two numbers and c is mean proportional between a and b

Then,

a : c = c : b

Question 19 :

Find the mean proportional between 10 and 40 ?

Solution:

Let, the mean proportional between 10 and 40 be ‘ a ‘

10 : a :: a : 40

(Product of extremes = Product of means)

Here, Extremes are 10 and 40

Means are a and a

10 x 40 = a x a

a² = 10 x 40 = 400

a = 20

Hence, the value of ‘a’ is 20

Ratio and Proportion Problems and Solutions for Class 7 – Continued proportion

Three numbers are said to be in Continued Proportion if the ratio of first and second number is equal to the ratio of second and third number.

If a, b, c are in continued proportion

Then,

a : b : : b : c

Question 20 :

If 12, 42, a are in continued proportion, find the value of a?

Solution:

Given –  12 , 42 , a are in continued proportion.

Then,

12 : 42 :: 42 : a

(Product of extremes = Product of means)

Here, Extremes are 12 and a

Means are 42 and 42

12 x a = 42 x 42

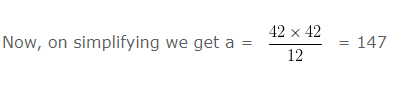
Hence, the value of ‘a’ is 147

Click here for Class 7 Chapterwise Explanations