Ratio and Proportion Class 6

Ratio and Proportion Class 6, deals with various concepts which are as under:-

• Converting Ratios to Simplest Form
• Equivalent Ratios
• Find the numbers when their ratio and sum are given
• Divide sum of money between two persons when ratio are given
• Divide sum of money among 3 persons when ratio are given
• Are the given number are in proportion
• Find the value of y when four numbers are in proportion

Ratio and Proportion Class 6 –   Converting Ratios to Simplest Form

In order to convert the given ratio to Simplest Form, we should follow the following steps : –

• Find the HCF of both the numerator and denominator
• Dividing Both numbers by their HCF

The result is the ratio in its simplest form.

Question 1:

Convert 16 : 28 into its simplest form

Explanation:

Convert the ratio 16 : 28 in its simplest form.

HCF of 16 and 28 is 4

Since, 16 : 28

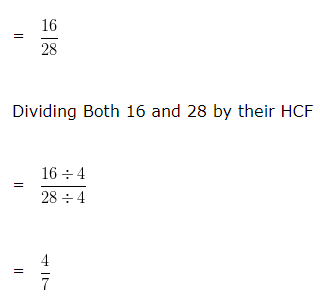
= 4 : 7

Hence, the simplest form of 16 : 28 is 4 : 7

Ratio and Proportion Class 6 –  Equivalent Ratios

In order to find Equivalent Ratios of any given ratio, we multiply or divide the numerator and denominator of the ratio by the same non zero number.

Question 2:

Find the Equivalent ratio of 2 : 5?

9/15, 5/2, 8/20 and 6/15

Explanation:

On multiplying or dividing each term of a ratio by the same non zero number, we get a ratio equivalent to the given ratio

For, 8/20

Both numerator and denominator of given fraction is multiplied by same nonzero number i.e 4

8/20 is an equivalent ratio of 2/5

9/15 is not an equivalent ratio of 2/5, As both 2 and 5 are not multiply by same non zero number

5/2 is not an equivalent ratio of 2/5. As both 2 and 5 are not multiply by same non zero number

6/15 is not an equivalent ratio of 2/5. As both 2 and 5 are not multiply by same non zero number

Ratio and Proportion Class 6 – Find the numbers when their ratio and sum are given

Question 3:

Two numbers are in the ratio 3 : 1 and their sum is 68. Find the numbers?

Explanation:

Let the required number be 3a and 1a

Since the sum of these two numbers is given, we can say that

3a + 1a = 68

4a = 68

a = 68/4

a = 17

So, the first number is 3a = 3 x 17

= 51

Second number is 1a = 1 x 17

= 17

Hence, two numbers are 51 and 17

Ratio and Proportion Class 6 – Divide sum of money between two persons when ratio are given

Question 4:

Divide ₹ 1500 among X and Y in the ratio 1 : 2

Explanation:

Total money = ₹ 1500

Given ratio = 1 : 2

Sum of ratio terms = ( 1 + 2 ) = 3

Give: 1/3 part of ₹ 1500 to X

Give: 2/3 part of ₹ 1500 to Y

that is,

X ‘s share = ₹ ( 1500 x 1/3) = ₹ 500

Y ‘s share = ₹ ( 1500 x 2/3) = ₹ 1000

Ratio and Proportion Class 6 – Divide sum of money among 3 persons when ratio are given

Question 5:

Divide ₹ 1200 among X , Y and Z in the ratio 2 : 3 : 1

Explanation:

Total money = ₹ 1200

Given ratio = 2 : 3 : 1

Sum of ratio terms = ( 2 + 3 + 1 ) = 6

X share = ₹ ( 1200 x 2/6) = ₹ 400

Y share = ₹ ( 1200 x 3/6) = ₹ 600

Z share = ₹ ( 1200 x 1/6) = ₹ 200

Ratio and Proportion Class 6 – Comparison of ratios

To Compare two Ratios, we should follow the following steps : –

• Write both the Ratios as Fractions
• Convert both the Fractions into Like Fraction:-
  – Find the L.C.M of denominator of both the Fractions
  – Make the denominator of each fraction equal to their L.C.M.
• In case of Like fractions, the number whose numerator is greater is larger.

Question 6:

Compare the ratios ( 2 : 1 ) and ( 1 : 4 )

Explanation:

We can write

( 2 : 1 ) = 2/1 and ( 1 : 4 ) = 1/4

Now, let us compare 2/1 and 1/4

LCM of 1 and 4 is 4

Making the denominator of each fraction equal to 4

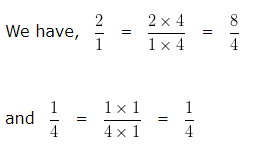
In case of Like fractions, the number whose numerator is greater is larger. Hence we can say 8/4 > 1/4

That is, 2/1 > 1/4

Hence, ( 2 : 1 ) > ( 1 : 4 )

Ratio and Proportion Class 6 – Four Numbers in Proportion

Let a, b, c, d are four numbers said to be in proportion.
then, a : b = c : d  or a : b :: c : d
here a and d are called the extreme terms or extremes.
b and c are called the middle terms or means.
When Four numbers are in proportion
then, Product of extremes = Product of means.
i.e, In proportion a : b :: c : d,
(a x d) = (b x c)

Ratio and Proportion Class 6 –  Are the given number are in proportion

Question 7:

Are 4 , 12 , 6 , 18 in proportion?

Explanation:

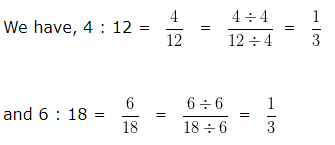
Since, 4 : 12 = 6 : 18

Hence, 4 , 12 , 6 , 18 are in Proportion

Alternative method: Product of extremes = Product of means

Here, Means are 12 and 6

Extremes are 4 and 18

Product of extremes = 4 x 18 = 72

Product of means = 12 x 6 = 72

Since, Product of extremes = Product of means

Hence, 4 , 12 , 6 , 18 are in Proportion

Ratio and Proportion Class 6 – Find the value of y when four numbers are in proportion

Question 8:

If 6 : 3 : : y : 2, find the value of y?

Explanation:

We know that, Product of means = Product of extremes

In the given numbers, we can say that 3 , y are means and 6 , 2 are extremes

3 x y = 6 x 2

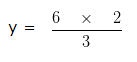
y = 4

Hence, y = 4

Click here for Class 6 Chapterwise Explanations