Properties of Integers | Closure, Commutative, Associative, Distributive

Properties of Integers, deals with various concepts which are as under:-

• Closure Property of Integers
• Commutative Property of Integers
• Associative Property of Integers
• Distributive Property of Integers
• Additive Identity
• Multiplicative Identity of Integers

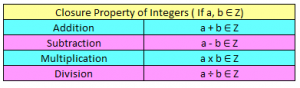
Closure Property of Integers

Closure Property under Addition of Integers

If we add any two integers,  the result obtained on adding the two integers, is always an integer. So we can say,  that integers are closed under addition.

Let us say ‘a’ and ‘b’ are two integers,  either positive or negative. When we add the two integers, their result would always be an integer, i.e (a + b) would always be an integer.

Example –

State whether (– 11) + 2 is closed under addition

Solution

– 11 + 2

– 9

Since both -11 and 2 are integers, and their sum, i.e (-9) is also an integer, we can say that integers are closed under addition.

Closure Property under Subtraction of Integers

If we subtract any two integers the result is always an integer, so we can say that integers are closed under subtraction.

Let us say ‘a’ and ‘b’ are two integers either positive or negative, their result should always be an integer, i.e (a + b) would always be an integer.

Example –

State whether (24 – 12) is closed under subtraction

Solution –

24 – 12

12

Since both 24 and -12 are integers, and their difference, i.e (12) is also an integer, we can say that integers are closed under subtraction.

Closure Property under Multiplication of Integers:

If we multiply any two integers the result is always an integer, so we can say that integers are closed under multiplication.

Let us say ‘a’ and ‘b’ are two integers either positive or negative, and if multiply it, their result should always be an integer, i.e [(-a) x b] and [a x (–b)] would always be an integer.

Example –

Show that (-30) x 11 closed under multiplication

Solution – 

– 30 x 11

-330

Since both -30 and 11 are integers, and their product, i.e (-330) is also an integer, we can say that integers are closed under multiplication.

Closure Property under Division of Integers:

If we divide any two integers the result is not necessarily an integer, so we can say that integers are not closed under division.

Let us say ‘a’ and ‘b’ are two integers, and if we divide them, their result ( a ÷ b ) is not necessarily an integer.

Example – 

State whether (14) ÷ 5 is closed under division.

Solution – 

(14) ÷ 5

8

Since both 14 and 5 are integers, but (14) ÷ 5 = 2.8 which is not an integer. Hence, we can say that integers are not closed under division.

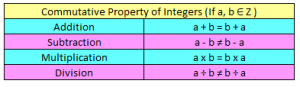
Commutative Property of Integers

Commutative Property under Addition of Integers:

• If we add two whole numbers say ‘a’ and ‘b’ the answer will always same, i.e if we add (2+3) = (3+2) = 5. So whole numbers are commutative under addition. Similarly if we apply this to integers, (-5+3) = (3+(-5))= -2, it also hold for all integers. So we can say that commutative property holds under addition for all integers.
• In generalise form for any two integers ‘a’ and ‘b’
  a + b = b + a

Example –

Show that -32 and 23 follow commutative property under addition.

Solution –

L.H.S = -32 + 23 = – 9

R.H.S = 23 + (-32) = 23 – 32 = – 9

So, L.H.S = R.H.S, i.e a + b = b + a

This means the two integers follow commutative property under addition.

Commutative Property under Subtraction of Integers:

• On contradictory, commutative property will not hold for subtraction of whole number say (5 – 6) is not equal to (6 – 5). Let us consider for integers (4) and (-1), the difference of two numbers are not always same.
  {4 – (-1) = 4 + 1= 5} and {(-1) – 4 = – 1 – 4 = -5}, so the difference of two integers are 5 and (-5) which are not equal so we can say that commutative property will not hold for subtraction of integers.

• In generalise form for any two integers ‘a’ and ‘b’
  (a – b) ≠ (b – a)

Example –

Check whether -88 and 22 follow commutative property under subtraction.

Solution –

L.H.S = -88 – 22 = – 110

R.H.S = 22 – (-88) = 22 + 88 = 110

So, L.H.S ≠ R.H.S

This means the two integers do not follow commutative property under subtraction.

Commutative Property under Multiplication of Integers:

• If we multiply two whole numbers say ‘a’ and ‘b’ the answer will always same, i.e if we multiply (2×3) = (3×2) = 6. So whole numbers are commutative under multiplication. Similarly if we apply this to integers, (-5×3) = (3x(-5))= -6, it also hold true for all integers. So we can say that commutative property holds under multiplication for all integers.
• In generalise form for any two integers ‘a’ and ‘b’
  a x b = b x a

Example –

Show that any two integers follow commutative property under multiplication.

Let us assume that the two integers are (-12) and 20,

L.H.S = (-12) x 20

= -240

R.H.S = 20 x (-12)

= -240

So, L.H.S = R.H.S, i.e ‘a x b’ = ‘b x a’

This means the two integers follow commutative property under multiplication.

Commutative Property under Division of Integers:

• Commutative property will not hold true for division of whole number say (12 ÷ 6) is not equal to (6 ÷ 12). Let us consider for integers say, (-14) and (7), the division of two numbers are not always same.
  [(-14) ÷ 7 = -2] and [7 ÷ (-14) = -0.5}, so the result of division of two integers are not equal so we can say that commutative property will not hold for division of integers.

• In generalise form for any two integers ‘a’ and ‘b’
  (a ÷ b) ≠ (b ÷ a)

Example – 

State whether (-12) and (-3) follow commutative law under division?

Solution – 

L.H.S = (-12) ÷ (-3) = 4

R.H.S = (-3) ÷ (-12) = 25

So, L.H.S ≠ R.H.S; i.e (a ÷ b) ≠ (b ÷ a)

This means the two integers do not follow commutative property under division.

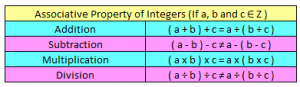
Associative Property of Integers

Associative Property under Addition of Integers:

• As commutative property hold for addition similarly associative property also holds for addition.
• In generalize form for any three integers say ‘a’, ’b’ and ‘c’
  a + (b + c) = (a + b) + c

Example – 

Show that (-6), (-1) and (3) are associative under addition.

Solution – 

L.H.S = – 6 + ( -1 + 3)

= – 6 + 2

= – 4

R.H.S = (- 6 + (-1)) + 3

= (- 6 – 1) + 3

= -7 + 3

= -4

So, L.H.S = R.H.S, i.e a + (b + c) = (a + b) + c

This means all three integers follow associative property under addition.

Associative Property under Subtraction of Integers:

• On contradictory, as commutative property does not hold for subtraction similarly associative property also does not hold for subtraction of integers.
• In generalize form for any three integers say ‘a’, ’b’ and ‘c’
  a – (b – c) ≠ (a – b) – c

Example –

Check whether (-6), (-1) and 3 follow associative property under subtraction.

Solution –

L.H.S = -6 – (-1 -3)

= -6 – (-4)

= -6 +4

= -2

R.H.S = (-6 – (-1)) – 3

= (-6 +1) – 3

= -5 -3

= -8

So, L.H.S ≠ R.H.S

This means all three integers do not follow associative property under subtraction.

Associative Property under Multiplication of Integers:

• As commutative property hold true for multiplication similarly associative property also holds true for multiplication.
• The associative property of multiplication does not depend on the grouping of the integers.
• In generalize form for any three integers say ‘a’, ’b’ and ‘c’
  a x (b x c) = (a x b) x c

Example –

Show that (-2), (-3) and 4 hold associative property for multiplication

Solution – 

L.H.S = (-2) x ( -3 x 4)

= -2 x -12

= 24

R.H.S = (-2 x -3) x 4

= 6 x 4

= 24

So, L.H.S = R.H.S; i.e a x (b x c) = (a x b) x c

This means all three integers follow associative property under multiplication.

Distributive Property of Integers:

Distributive properties of multiplication of integers are divided into two categories, over addition and over subtraction.

1. Distributivity of multiplication over addition hold true for all integers.
In generalize form for any three integers say ‘a’, ’b’ and ‘c’
a x (b + c) = (a x b) + (a x c)

Example –

Show that (-2), 3 and 5 follow distributive property of multiplication over addition.

Solution – 

L.H.S = -2 x (3 + 5)

= -2 x 8

= -16

R.H.S = (-2 x 3) + (-2 x 5)

= -6 + (-10)

= -6 -10

= -16

So, L.H.S = R.H.S; i.e a x (b + c) = (a x b) + (a x c)

This means that distributive property of multiplication over addition holds true for all integers.

2. Distributivity of multiplication over subtraction hold true for all integers.
In generalize form for any three integers say ‘a’, ’b’ and ‘c’
a x (b – c) = (a x b) – (a x c)

Example – 

Show that (-5), (-4) and (-2) follow distributive property of multiplication over subtraction.

L.H.S = -5 x (-4 – (-2))

= -5 x (-4 + 2)

= -5 x -2

= 10

R.H.S = (-5 x -4) – (-5 x -2)

= 20 – 10

= 10

So, L.H.S = R.H.S; i.e a x (b – c) = (a x b) – (a x c)

This means that distributive property of multiplication over subtraction holds true for all integers.

Additive Identity:

When we add zero to any whole number we get the same number, so zero is additive identity for whole numbers. Similarly if we add zero to any integer we get the back the same integer whether the integer is positive or negative. In general for any integer ‘a’

a + 0 = 0 + a = a

Multiplicative Identity of Integers:

• When we multiply any positive or negative integer by 1 the answer will remains same the integer only.
• In generalise form, for any integer ‘a’
  a x 1 = 1 x a = a