Remainder Theorem (शेषफल प्रमेय)
Let p(x) be any polynomial of degree greater than or equal to 1 and let ‘a’ be any real number. If p(x) is divided by the linear polynomial (x – a), then the remainder is p(a).
Proof: Let p(x) be any polynomial. Suppose that when p(x) is divided by x – a, then quotient is q(x) and remainder is r(x). i.e.
Since the degree of (x – a) is 1 then the degree of r(x)is less than the degree of x – a, the degree of r(x) = 0. This means that r(x) is a constant, say r.
So for every value of x, r(x) = r.
therefore, p(x) = (x – a)q(x) + r
If x = a, then the equation will give us:
p(a) = (a – a)q(a) + r = 0 + r
p(a) = 0
Which proves the theorem.
Polynomial Remainder Theorem Examples With Answers
Example 1:-
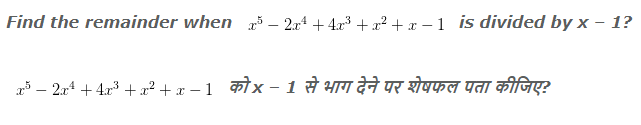
Explanation:

So the remainder will be 4.
Example 2:-
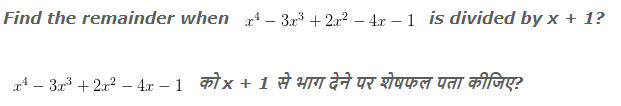
Explanation:

p(-1) = 1+3+2+4-1
So the remainder will be 9.
Example 3:-
Check whether x – 2 is a factor of x³+x²-2x-8
जांच कीजिए कि x – 2, x³+x²-2x-8 का एक गुणानखण्ड है या नहीं?
Explanation:
If x – 2 is a factor of x³+x²-2x-8 then when we will divide x³+x²-2x-8 by x – 2 then remainder must be zero.
So by remainder theorem:
p(x) = x³+x²-2x-8 and the zero of x – 2 is 2.
So by remainder theorem we can say that the remainder will be p(2).
p(2) = 2³+2²-2(2)-8
= 8+4-4-8
= 0
So there remainder is zero that means x – 2 is a factor of x³+x²-2x-8
1 thought on “Polynomial Remainder Theorem Examples With Answers”
I was recommended this website by my cousin. I’m not sure whether this post is written by him as nobody else know such detailed about my trouble. You are incredible! Thanks!