Perimeter And Area Questions For Class 6

Perimeter And Area Questions For Class 6, deals with various concepts which are as under:-




Perimeter And Area Questions For Class 6 – Perimeter of Rectangle

Perimeter of Rectangle is equal to twice of Sum of its length and breadth.

Perimeter of Rectangle Formula

Perimeter of Rectangle = 2 ( Length of Rectangle + Breadth of Rectangle )

Question 1

Find the perimeter of a rectangle in which:
length = 12 cm and  breadth = 5 cm

Explanation:

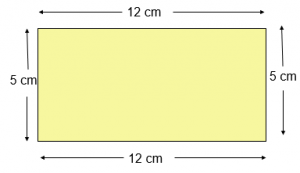
Given:
Length = 12 cm
Breadth = 5 cm
Perimeter of Rectangle = 2 ( l + b ) units
Perimeter of Rectangle = 2 ( 12 + 5 ) cm    (Here, Length = 12 cm , Breadth = 5 cm )
Perimeter of Rectangle = ( 2 x 17 ) cm
Perimeter of Rectangle = 34 cm
Hence, Perimeter of Rectangle is 34 cm

 

Perimeter And Area Questions For Class 6 – Perimeter of a Square

Perimeter of a Square is equal to four times of its side.

Perimeter of Square = 4 x Length of each side

Question 2

Find the perimeter of a square, each of whose side is 14 cm ?

Explanation:

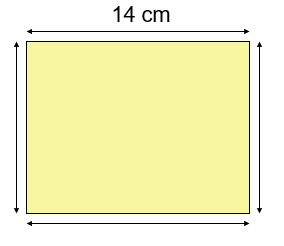
Square is a four sided polygon having all four sides equal in length.

Given:
Side = 14 cm
Perimeter of square = ( 4 x Length of each side ) units
Perimeter of square = ( 4 x 14 ) cm
Perimeter of square = 56 cm
Hence, Perimeter of square is 56 cm




Perimeter And Area Questions For Class 6 – Perimeter of Triangle

Perimeter is the sum of all the sides of a closed figure.
Triangle is a three-sided polygon.
Perimeter of a triangle is equal to the sum of all the three sides of the triangle.
Perimeter of Triangle = Sum of its 3 sides

Question 3

Find the perimeter of a triangle of sides 11 cm, 5 cm and 8 cm ?

Explanation

Given:
Ist side = 11 cm
IInd side = 5 cm
IIIrd side = 8 cm
Perimeter of triangle = Sum of its sides
Perimeter of triangle = ( Ist side + IInd side + IIIrd side ) cm
Perimeter of triangle = ( 11 + 5 + 8 ) cm
Perimeter of triangle = 24 cm
Hence, Perimeter of triangle is 24 cm

 

Perimeter And Area Questions For Class 6 – Perimeter of an Equilateral Triangle

Perimeter is the sum of all the sides of a closed figure.
An equilateral triangle is a triangle having all three sides equal in length.
Perimeter of an equilateral triangle is equal to three times the length of a side of a triangle.
Perimeter of an Equilateral Triangle = 3 x Length of each side

Question 4

Find the perimeter of an equilateral triangle of side 9cm

Explanation

An equilateral triangle is a triangle having all three sides equal in length.
Length of each side of an equilateral triangle = 9 cm
Perimeter of an equilateral triangle = ( 3 x Length of each side ) units
Perimeter of an equilateral triangle = ( 3 x 9 ) cm
Perimeter of an equilateral triangle = 27 cm
Hence, Perimeter of an equilateral triangle is 27 cm




Perimeter And Area Questions For Class 6 – Perimeter of a Regular Pentagon

Perimeter is the sum of all the sides of a closed figure
A regular pentagon is a five-sided polygon.
All the five sides of regular pentagon are equal.
Perimeter of a Regular Pentagon is equal to five times the length its side.
Perimeter of Regular Pentagon = 5 x Length of each side

Question 5

Find the perimeter of a regular pentagon of side 10cm

Explanation

A regular pentagon is a five sided polygon.
All the five sides of regular pentagon are equal.
So, Length of each side of regular pentagon = 10cm
Perimeter of a regular pentagon = ( 5 x Length of each side ) units
= ( 5 x 10 ) cm
= 50 cm
Hence, Perimeter of a regular pentagon is 50 cm

 

Perimeter And Area Questions For Class 6 – Perimeter of a Regular Octagon

Perimeter is the sum of all the sides of a closed figure
A regular octagon is an eight-sided polygon.
All eight sides of regular octagon are equal.
Perimeter of a Regular Octagon is equal to eight times the length its side.
Perimeter of Regular Octagon = 8 x Length of each side

Question 6

Find the perimeter of a regular octagon of side 10cm

Explanation

A regular octagon is an eight sided polygon.
All eight sides of regular octagon are equal.
So, Length of each side of regular octagon =10cm
Perimeter of a regular octagon = ( 8 x Length of each side ) units
= ( 8 x 10 ) cm
= 80 cm
Hence, Perimeter of a regular octagon is 80 cm




Perimeter And Area Questions For Class 6 – Perimeter of a Regular Decagon

Perimeter is the sum of all the sides of a closed figure
A regular decagon is a ten-sided polygon whose all ten sides are equal in length.
Perimeter of a Regular Decagon is equal to ten times the length its side.
Perimeter of Regular Decagon = 10 x Length of each side

Question 7

Find the perimeter of a regular decagon of side 4.5 cm

Explanation

A regular decagon is a ten sided polygon that has all ten sides equal in length
Length of a regular decagon =4.5 cm
Perimeter of a regular decagon =(10 x Length of each side)units
=(10 x 4.5) cm
=45 cm
Hence, Perimeter of a regular decagon is 45 cm

 

Perimeter And Area Questions For Class 6 – Area of Rectangle

Area of Rectangle is equal to the product of its length and breadth.

Area of Rectangle = Length x Breadth

Question 8

Find the area of rectangle in which: length = 6 cm and breadth = 7 cm

Explanation

Given,
length = 6 cm
breadth = 7 cm
Area of rectangle = ( length x breadth )
= ( 6 x 7 ) cm²
= 42 cm²

Hence, the area of rectangle is 42 cm²

Perimeter And Area Questions For Class 6 – Finding cost of fencing of a rectangular field

Question 9

Find the cost of fencing of a rectangular field 20 m long and 35 m wide at ₹ 6 per metre.

Explanation

Length of the field = 20 m
Breadth of the field = 35 m
Perimeter of the field = 2 ( l+b ) units
= 2 ( 20 + 35 ) m
= ( 2 x 55 ) m
= 110 m

Cost of fencing per metre = ₹ 6

Total cost of fencing = ₹ ( 110 x 6 )
= ₹ 660




Perimeter And Area Questions For Class 6 – Finding Length of rope fenced around Rectangular Field

Question 10

The length and the breadth of a rectangular field are 40 m and 60 m respectively. It is fenced with 2 round of rope. Find the length of the rope.

Explanation

Length of the field = 40 m
Breadth of the field = 60 m
Perimeter of the field = 2 (l+b) units
= 2 ( 40 + 60 ) m
= ( 2 x 100 ) m
= 200 m

Total length of rope = 2 x Perimeter of the field
= ( 2 x 200 ) m
= 400 m

 

Perimeter And Area Questions For Class 6 – Area of Square

Area of Square is equal to (length of its side x length of side).

Area of Square = ( side x side )  = (side)²

Question 11

Find the area of a square plot of side 2.5 cm

Explanation

Sides of square = 2.5 cm

Area of square = ( side x side ) cm²

= ( 2.5 x 2.5 ) cm²

= 6.25 cm²

Hence, the area of square plot is 6.25 cm²

 

Perimeter And Area Questions For Class 6 – Finding Circumference of the circle when radius is given

Circumference of a circle is the measure of the length of the circle.

Circumference of a circle = 2Ï€r

Question 12

Find the circumference of a circle of radius 49 cm?

Explanation

The radius of given circle is r = 49 cm

Circumference of the circle = 2Ï€r

= ( 2 x 22/7 x 49 ) cm

= 308 cm

Hence, the circumference of the given circle is 308 cm




Perimeter And Area Questions For Class 6 – Finding Circumference of the circle when diameter is given

Circumference of a circle is the measure of the length of the circle.

Circumference of a circle = 2Ï€r

Question 13

Find the circumference of a circle, whose diameter is 56 cm?

Explanation

The diameter of given circle = 56 cm

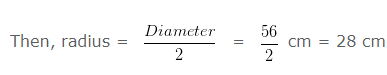
Circumference of circle = 2Ï€r

= ( 2 x 22/7 x 28 ) cm

= 176 cm

Hence, the circumference of the given circle is 176 cm

 

Perimeter And Area Questions For Class 6 – Radius of a Circle

Question 14

Find the radius of the circle whose circumference is 132 cm?

Explanation

Let, the radius of the given circle be r cm

As we know that,

Circumference of the circle = 2Ï€r cm

Given,

Circumference of a circle = 132cm

2Ï€r = 132 (from above)

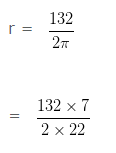
= 21cm

Hence, the radius of the circle = 21cm

 

Perimeter And Area Questions For Class 6 –  Finding Diameter of a circle when circumference is given

Question 15

Find the diameter of the circle whose circumference is 264 cm?

Explanation

Let, the radius of the given circle be r cm

As we know that,

Circumference of the circle = 2Ï€r cm

Given,

Circumference of a cicle = 264cm

Therefore,

2Ï€r = 264 (from above)

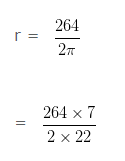
= 42cm

Diameter of the circle = 2r

= (2 x 42)cm

= 84cm

Hence, the Diameter of the circle is 84 cm

 

Perimeter And Area Questions For Class 6 – Problem-based on circumference of a circle

Question 16

The diameter of a wheel of a car is 42 cm. Find the distance covered by the car during the time in which the wheel makes 1600 revolutions?

Explanation

Radius of the wheel = 42/2 cm = 21 cm

Circumference of the wheel = 2Ï€r

= 132 cm

= 1.32 m ( As we know that, 1 m = 100 cm )

Distance covered by wheel in 1 revolution = Circumference of the wheel

Distance covered by wheel in 1 revolution = 1.32 m

Distance covered by wheel in 1600 revolutions = ( 1.32 x 1600 ) m

= 2112 m

= 2.112 km ( As we know that, 1 m = 1000 km )

Hence, Distance covered by wheel in 1600 revolutions is 2.112 km




Perimeter And Area Questions For Class 6 – Finding Perimeter of Rectangle when Area & Breadth is given

Question 17

The area of a rectangle is 832 cm² and its breadth is 26 cm. Find the perimeter of the rectangle.

Explanation

Given
Area = 832 cm²
breadth = 26 cm

Perimeter of the rectangle = 2 x ( l + b ) cm
= 2 x ( 26 + 32 ) cm
= ( 2 x 58 ) cm
= 116 cm

Hence, the perimeter of the rectangle is 116 cm

 

Perimeter And Area Questions For Class 6 – Finding Perimeter of Rectangle when Area & Length are given

Question 18

The area of a rectangle is 85 cm² and its length is 5 cm . Find the perimeter of the rectangle.

Explanation

Given
Area = 85 cm²
length = 5 cm

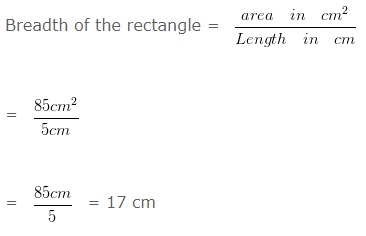
Perimeter of the rectangle = 2 x ( l + b ) cm
= 2 x ( 5 + 17 ) cm
= ( 2 x 22 ) cm
= 44 cm

Hence, perimeter of the rectangle is 44 cm

 

Perimeter And Area Questions For Class 6 – Problem based on Perimeter of rectangle

Question 19

The length and the breadth of a rectangle are in the ratio 2 : 5 . If its perimeter is 28 m , find its dimensions.

Explanation

Let, length and breadth be 2y m and 5y m

Since, perimeter of rectangle = 2 (l+b) units
= 2 ( 2 y + 5 y ) m
= ( 2 x 7 y ) m
= 14ym

But, perimeter of rectangle = 28 m

Since, 14 y = 28
y = 28/14

y = 2

So, length = ( 2 x 2 ) m = 4 m
breadth = ( 5 x 2 ) m = 10 m




Perimeter And Area Questions For Class 6 – Problem based on cost of carpeting the room

Question 20

A room is 48 m long and 18 m broad. Find the cost of carpeting the room with a carpet of width  18 m at the rate of ₹ 50 per metre.

Explanation

Length of the room = 48 m
Breadth of the room = 18 m

Area of the floor of the room = ( 48 x 18 ) m²
= 864 m²

Area of carpet required = 864 m²

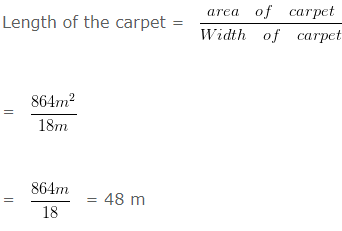
Rate of carpeting = 50 per metre.
Cost of carpeting = ₹ ( 48 x 50 ) = ₹ 2400

Click here for Class 6 Chapterwise Explanations

NCERT Solutions for Class 6

CBSE Notes for Class 6

Worksheets for Class 6

Leave a Comment