NCERT Solutions for Class 9 Maths Chapter 9 Exercise 9.3

Download NCERT Solutions for Class 9 Maths Chapter 9 Exercise 9.3 – Areas of Parallelograms And Triangles. This Exercise contains 16 questions, for which detailed answers have been provided in this note. In case you are looking at studying the remaining Exercise for Class 9 for Maths NCERT solutions for Chapter 10 or other Chapters, you can click the link at the end of this Note.

NCERT Solutions for Class 9 Maths Chapter 9 Exercise 9.3

NCERT Solutions for Class 9 Maths Chapter 9 Exercise 9.3

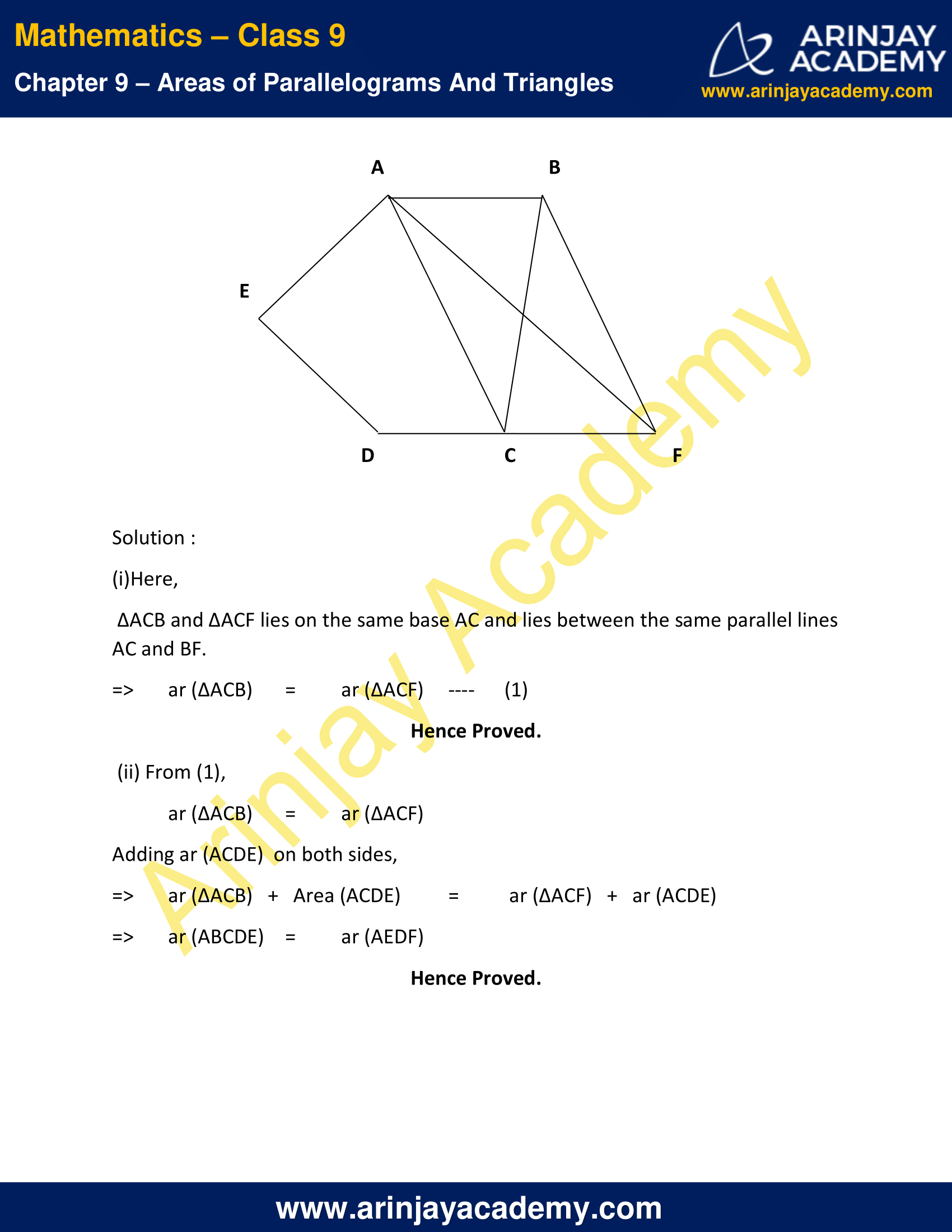
1. In given figure, E is any point on median AD of a ∆ ABC. Show that
ar (ABE) = ar (ACE).

Solution :

Given that, AD is the median of ∆ ABC, BD = DC
=> ar (∆ ABD ) = ar (∆ ADC )
=> ar (∆ ABE ) + ar (∆  EBD ) = ar (∆ ACE ) +   ar (∆ ECD )   ….(1)
It can be clearly observed that, in the ∆ EBC, ED is the median.
=> ar ( ∆ EBD ) = ar ( ∆ ECD )  ….(2)
On subtracting equation 2 from equation 1, we get
ar ( ∆ ABE ) = ar ( ∆ ACE )
Hence Proved.

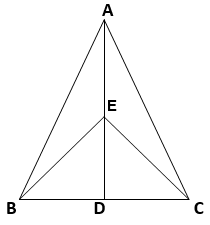
2. In a triangle ABC, E is the mid-point of median AD. Show that
ar (BED) = (1/4) ar(ABC)

Solution :

Given AD is the median of the triangle ABC,
=> ar ( ∆ ABD ) = 1/2 ar ( ∆ ABC )  ….(1)
And also, from the figure
BE is the median of the triangle ABD ( given that E is the midpoint of AD)
=> ar ( ∆ ABE ) = ar ( ∆ BED ) = 1/2 ar ( ∆ ABD )  ….(2)
By substituting (1) in (2),
=> ar ( ∆ BED )   = 1/2 x 1/2 ar ( ∆ ABC )
ar ( ∆ BED ) = 1/4 ar( ∆ ABC )
Hence Proved.

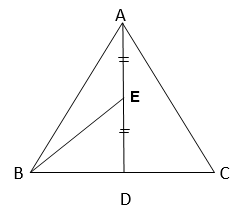
3. Show that the diagonals of a parallelogram divide it into four triangles of equal area.

Solution :

ABCD is a parallelogram
Diagonals of the parallelogram ABCD bisect each other at O.
O is the midpoint of AC and BD
In ∆ACD, OD is the median.
=> ar(∆ AOD ) = ar (∆ COD )  …(1)
In ∆DBC, OC is the median.
=> ar(∆ COD ) = ar (∆ BOC )   …(2)
Similarly, In ∆ ABC, OB is the median.
=>  ar (∆ AOB ) = ar (∆ BOC )  …(3)
From equation (1), (2) and (3), we get
ar (∆ AOB) = ar (∆ BOC) = ar (∆ COD) = ar (∆AOD)
Hence Proved.

4. In given figure, ABC and ABD are two triangles on the same base AB. If line- segment CD is bisected by AB at O, show that ar(ABC) = ar (ABD).

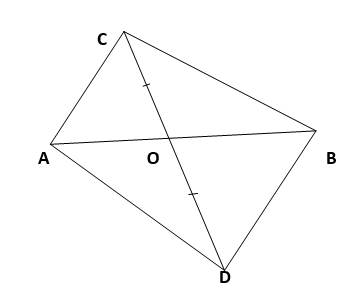
Solution :

In triangle ACD,
CD is bisected by AB at O.
=> AO is the median of ∆ ACD.
=> ar (∆ ACO ) = ar (∆ ADO )  ….(1)
In triangle BCD,
BO is the median.
=> ar (∆ BCO ) = ar (∆ BDO )   ….(2)
By adding (1) and (2), we obtain
ar (∆ ACO ) + ar (∆ BCO ) = ar (∆ ADO ) + ar (∆ BDO )
=> ar (∆ ABC ) = ar (∆ ABD )
Hence Proved.

5. D, E and F are respectively the mid-points of the sides BC, CA and AB of a ∆ABC.
Show that:
(i) BDEF is a parallelogram.
(ii) ar (DEF) = (1/4) ar (ABC)
(iii) ar (BDEF) = (1/2) ar (ABC)

Solution :

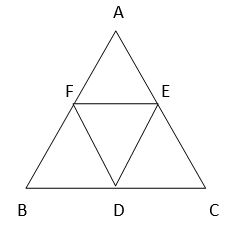
(i) We know that,
Line joining the mid-points of two sides of a triangle is parallel to the third and half of it.
=> FE || BC & FE = 1/2 BC
Since D is the mid-point of BC,   BD  =  (1/2) BC
=> FE || BD   &  FE = BD —-  (1)
Similarly,
DE || AB & DE = (1/2) AB
=> DE║BF  & DE = BF   …. (2)
From (1) & (2),
FE || BD & DE || BF
And  FE = BD  & DE = BF
=> BDEF is a parallelogram.
Hence Proved.

(ii) Since BDEF is a parallelogram and FD is the diagonal of the parallelogram,
=>  ar (∆ FBD) = ar (∆ DEF)   …(3)
[Diagonals of parallelogram divides it in two triangles of equal area]
Similarly,
AFED is also a parallelogram and EF is the diagonal
=> ar (∆ AFE) = ar (∆ DEF)  ….(4)
Similarly,
FECD is also a parallelogram and ED is the diagonal
=> ar (∆ ECD) = ar (∆ DEF)  ….(5)
We know that,
ar (∆ ABC)  =  ar (∆ DEF)  +  ar (∆ ECD)  +  ar (∆AFE)  + ar (∆ FBD)  —- (6)
Substituting (3), (4), (5) in (6)
ar (∆ ABC) = 4 ar (∆ DEF)
=> ar (∆ DEF) = (1/4) ar (∆ ABC)  ….(7)
Hence Proved.

(iii) From (3) & (7),
We can say that,
ar (∆ DEF) = ar (∆ FBD) = (1/4) ar (∆ ABC)
We also Know that,
ar ( //gm BDEF) = ar (∆ FBD) + ar (∆ DEF)
=> ar (//gm BDEF) = 2 x (1/4) ar (∆ ABC)
=> ar (//gm BDEF) = (1/2) ar (∆ ABC)
Hence Proved.

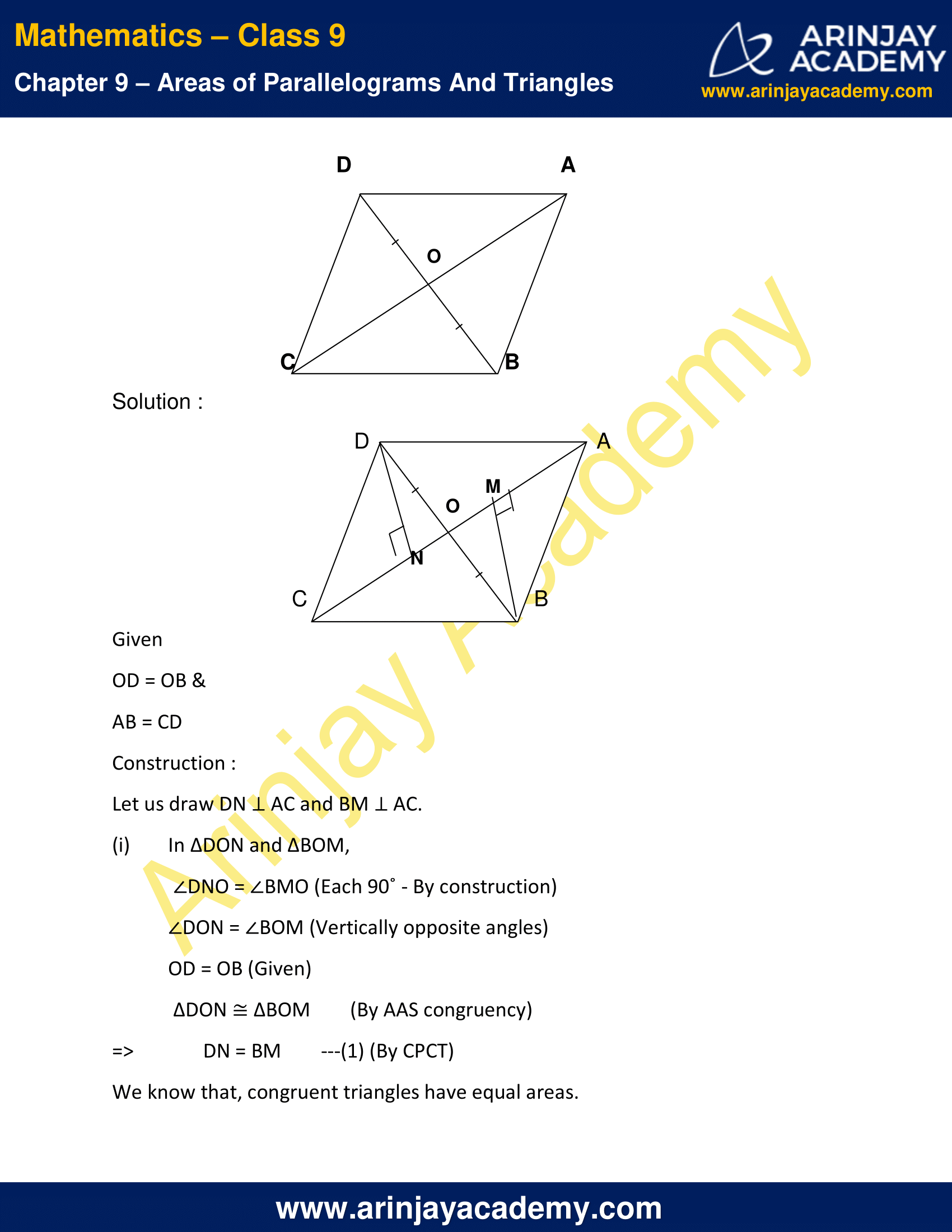
6. In given figure, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that:
(i) ar (DOC) = ar (AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB or ABCD is a parallelogram.
[Hint: From D and B, draw perpendiculars to AC.]

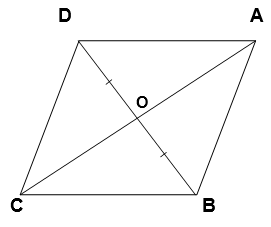
Solution :

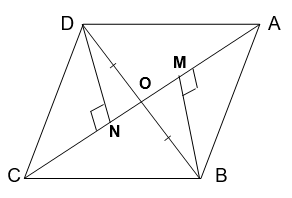
Given
OD = OB &
AB = CD
Construction :
Let us draw DN ⊥ AC and BM ⊥ AC.
(i) In ∆DON and ∆BOM,
∠DNO = ∠BMO (Each 90˚ – By construction)
∠DON = ∠BOM (Vertically opposite angles)
OD = OB (Given)
∆DON ≅ ∆BOM (By AAS congruency)
=> DN = BM  ….(1) (By CPCT)
We know that, congruent triangles have equal areas.
=> ar (∆DON) = ar (∆BOM)  ….(2)
From the triangles, DNC and BMA,
∠DNC = ∠BMA (Each 90˚ – By construction)
CD = AB (given)
DN = BM ( From (1) )
=> ∆DNC ≅ ∆BMA (By R.H.S congruency)
=> ar (∆DNC) = ar (∆BMA)  ….(3)
On adding (2) & (3),
we get,
ar (∆DON) + ar (∆DNC) = ar (∆BOM) + ar (∆BMA)
=> ar (∆DOC) = ar (∆AOB)
Hence Proved.

(ii) We get,
ar (∆DOC) = ar (∆AOB)
Adding ar( ∆ OCB ) on both sides
=> ar (∆DOC) + ar (∆OCB) = ar (∆AOB) + ar (∆OCB)
=> ar (∆DCB) = ar (∆ACB)
Hence Proved.

(iii) We get,
ar (∆DCB) = ar (∆ACB)
If two triangles have the same base and equal areas, then these will lie between the same parallels.
=> DA || CB  ….(4)
& AD = BC    (Given)
In quadrilateral ABCD, one pair of opposite sides is equal (AB = CD) and the other pair of opposite sides are parallel (DA || CB).
=> ABCD is a parallelogram.
Hence Proved.

7. D and E are points on sides AB and AC respectively of ∆ ABC such that ar (DBC) = ar (EBC). Prove that DE || BC

Solution :

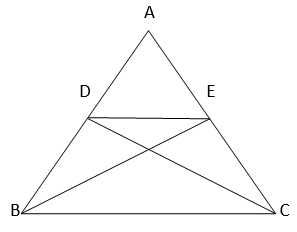
Since,  ∆BCE and ∆BCD are lies on a common base (BC) & also have equal areas(given),  ∆BCE & ∆BCD will lie between the same parallel lines.
=> DE || BC.
Hence Proved.

 8. XY is a line parallel to side BC of a triangle ABC. If BE || AC and CF || AB meet XY at E and F respectively,
show that ,
ar (ABE) = ar (ACF)

Solution :     

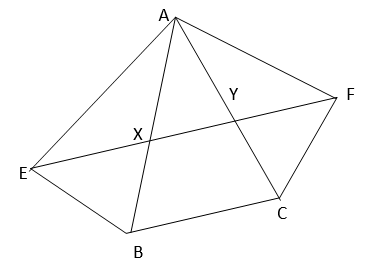
It is given that,
XY || BC => EY || BC
BE || AC => BE || CY
=> EBCY is a parallelogram.
It is given that,
XY || BC => XF || BC
FC || AB => FC || XB
=> BCFX is a parallelogram.
Parallelograms EBCY and BCFX are on the same base (BC) and lies between the same parallel lines (BC and EF)
=>  ar ( //gm EBCY ) = ar ( //gm BCFX )  …(1)
From //gm EBCY and ∆AEB,
These lies on the same base (BE) and lies between the same parallel lines (BE and AC)
=> ar (∆ABE) = (1/2) ar ( //gm EBCY ) ….(2)
From //gm  BCFX and ∆ACF
These are on the same base (CF) and between the same parallel lines (CF and AB)
=> ar (∆ACF) = (1/2) ar ( //gm BCFX )  ….(3)
From (1), (2) & (3),
We get,
ar (∆ABE) = ar (∆ACF)
Hence Proved.

9. The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed (see the following figure).
Show that ar (ABCD) = ar (PBQR).
[Hint: Join AC and PQ. Now compare area (ACQ) and area (APQ)]

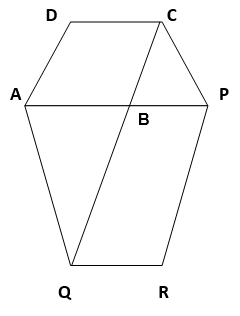
Solution :

Construction :         Join AC & PQ

Here,
∆ACQ and ∆AQP are on the same base AQ and between the same parallels AQ and CP
=> ar (∆ACQ) = ar (∆APQ)
Subtracting ar (∆ABQ ) on both sides,
=> ar (∆ACQ)  – ar (∆ABQ) = ar (∆APQ) – ar (∆ABQ)
=> ar (∆ABC) = ar (∆QBP)  ….(1)
Since AC and PQ are diagonals of parallelograms ABCD and PBQR respectively,
ar (∆ABC) = ( 1/2) ar ( //gm ABCD )   …(2)
=> ar (∆QBP) = (1/2) ar ( //gm PBQR )  …(3)
From (1), (2) & (3),
We get,
(1/2) ar ( //gm ABCD) = (1/2) ar ( //gm PBQR)
=> ar ( ABCD ) = ar ( PBQR )
Hence Proved.

10. Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that ar (AOD) = ar (BOC).

Solution :

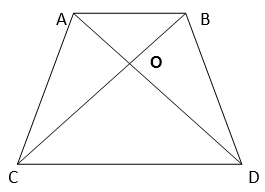
Here, it can be observed that ∆DAC and ∆DBC lie on the same base DC and between the same parallel lines AB and CD.
=> ar (∆DAC) = ar (∆DBC)
Subtracting ar (∆DOC) from both the sides,
=> ar (∆DAC) – ar (∆DOC) = ar (∆DBC) – ar (∆DOC)
=> ar (∆AOD) = ar (∆BOC)
Hence Proved.

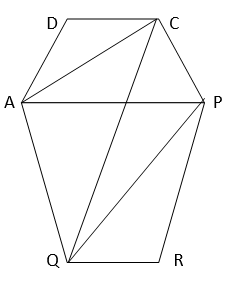
 11. In given figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F.
Show that
(i) ar (ACB) = ar (ACF)
(ii) ar (AEDF) = ar (ABCDE)

                                               

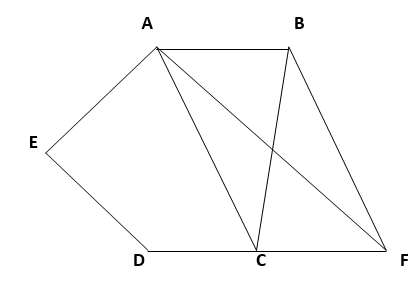
Solution :

(i)Here,
∆ACB and ∆ACF lies on the same base AC and lies between the same parallel lines AC and BF.
=> ar (∆ACB) = ar (∆ACF)  ….(1)
Hence Proved.

(ii) From (1),
ar (∆ACB) = ar (∆ACF)
Adding ar (ACDE)  on both sides,
=> ar (∆ACB) + Area (ACDE) = ar (∆ACF) + ar (ACDE)
=> ar (ABCDE) = ar (AEDF)
Hence Proved.

12. A villager Itwaari has a plot of land of the shape of a quadrilateral. The Gram Panchayat of the village decided to take over some portion of his plot from one of the corners to construct a Health Centre. Itwaari agrees to the above proposal with the condition that he should be given equal amount of land in lieu of his land adjoining his plot so as to form a triangular plot. Explain how this proposal will be implemented.

Solution :

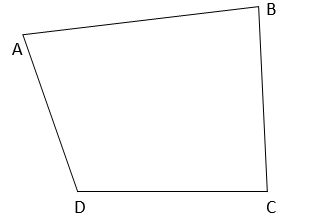
Let ABCD be the shape of plot of land of itwaari
The proposal can be made as follows,
Join BD,
Draw a line parallel to BD through A and let it meet the CD at E.

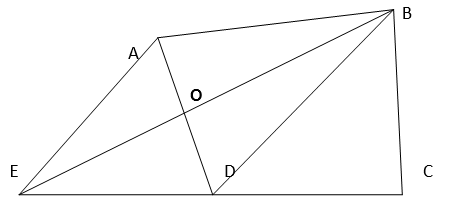
From the triangles DEB & DAB,
Both the triangles lie on the same base DB and lies between the same parallel lines AE & BD ( AE|| BD is through construction )
=> ar (∆ DEB ) = ar (∆ DAB )
Subtracting ar(∆ DOB ) from both the sides,
=> ar (∆ DEB ) – ar (∆ DOB ) = ar (∆ DAB ) – ar (∆ DOB )
=> ar (∆ DOE ) = ar (∆ AOB )
So, he can give his AOB area and get DOE area to complete his form in a triangular shape.

13. ABCD is a trapezium with AB || DC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar (ADX) = ar (ACY). [Hint: Join CX.]

Solution :

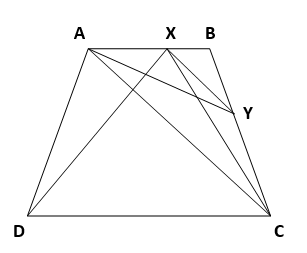
Consider triangles ADX and ACX,
Both the triangles lies on the same base ( AX ) and lies between the same parallel lines ( AB & CD ).
=> ar (∆ ADX ) = ar (∆ ACX )   …(1)
Consider the triangles ACX and ACY,
Both the triangles lies on the same base ( AC  ) and lies between the same parallel lines ( AC & XY ).
=> ar (∆ ACY ) = ar (∆ ACX )    ….(2)
From (1) & (2),
=> ar (∆ ADX) = ar (∆ ACY)
Hence Proved.

14. In given Figure, AP || BQ || CR. Prove that ar (AQC) = ar (PBR

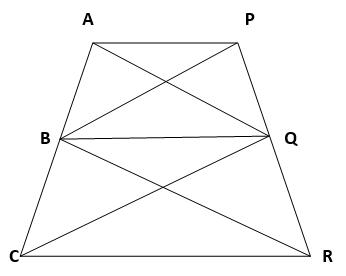
Solution :

Given : AP || BQ || CR
Consider the triangles ABQ & PBQ,
Both the triangles lies on the same base ( BQ ) and lies between the same parallel lines ( AP & BQ ).
=> ar ( ∆ ABQ ) = ar (∆ PBQ )  …(1)
Consider the triangles CBQ & RBQ,
Both the triangles lies on the same base (BQ) and lies between the same parallel lines ( BQ & CR ).
=> ar (∆ CBQ ) = ar (∆ RBQ )  …(2)
On adding equations (1) & (2),
=> ar(∆ ABQ ) +  ar (∆ CBQ ) = ar (∆ PBQ )  +  ar (∆ RBQ )
=> ar (∆ AQC ) = ar (∆ PBR )
Hence Proved.

15. Diagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD) = ar (BOC). Prove that ABCD is a trapezium

Solution :

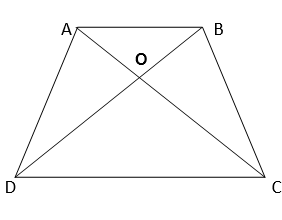
Given,
ar(∆ AOD ) = ar (∆ BOC )
Adding  ar(∆ AOB ) on both the sides.
=> ar (∆ AOD )  +  ar(∆ AOB ) = ar (∆ BOC )  +  ar (∆ AOB )
=> ar (∆ ABD ) = ar (∆ ABC )
Since the triangles ABD & ABC are on the same base and have equal area, they lies between the same parallel lines,  AB & CD
=> AB || CD
Therefore, ABCD is a trapezium
Hence Proved.

16. In given figure, ar (DRC) = ar (DPC) and ar (BDP) = ar (ARC). Show that both the quadrilaterals ABCD and DCPR are trapeziums.

 

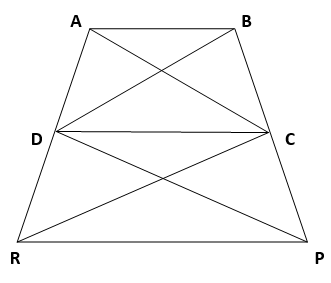
Solution :

Given,
ar (∆ DRC ) = ar (∆ DPC )  ….(1)
ar(∆ BDP ) = ar (∆ ARC )  ….(2)
(1)  =>   Both the triangles DRC and DPC lies on the same base DC and lies between the same parallel lines CD and PR
=> In a quadrilateral when two sides are parallel then it is a trapezium.
Since CD and RP are parallel in the quadrilateral CDPR,
CDPR is a trapezium.
Hence Proved

(2) can be written as
ar(∆ BDC ) + ar (∆ DPC ) = ar (∆ ADC ) + ar (∆ DRC)
Since ar(∆ DPC ) = ar (∆ DRC )  (Form (1) )
=> ar (∆ BDC ) = ar (∆ ADC )   …(3)

(3)   =>  Both the triangles lies on the same base DC and lies between the same parallel lines AB & CD
In the quadrilateral ABCD, AB || CD
=>  ABCD is a trapezium
Hence Proved.

NCERT Solutions for Class 9 Maths Chapter 9 Exercise 9.3 – Areas of Parallelograms And Triangles, has been designed by the NCERT to test the knowledge of the student on the topic – Triangles on the same Base and between the same Parallels

The next Exercise for NCERT Solutions for Class 9 Maths Chapter 10 Exercise 10.1 – Circles can be accessed by clicking here.

• Maths – NCERT Solutions Class 9
• NCERT Solutions Class 9

Download NCERT Solutions for Class 9 Maths Chapter 9 Exercise 9.3 – Areas of Parallelograms And Triangles