Download NCERT Solutions for Class 9 Maths Chapter 7 Exercise 7.3 – Triangles. This Exercise contains 5 questions, for which detailed answers have been provided in this note. In case you are looking at studying the remaining Exercise for Class 9 for Maths NCERT solutions for Chapter 7 or other Chapters, you can click the link at the end of this Note.
NCERT Solutions for Class 9 Maths Chapter 7 Exercise 7.3 – Triangles





NCERT Solutions for Class 9 Maths Chapter 7 Exercise 7.3 – Triangles
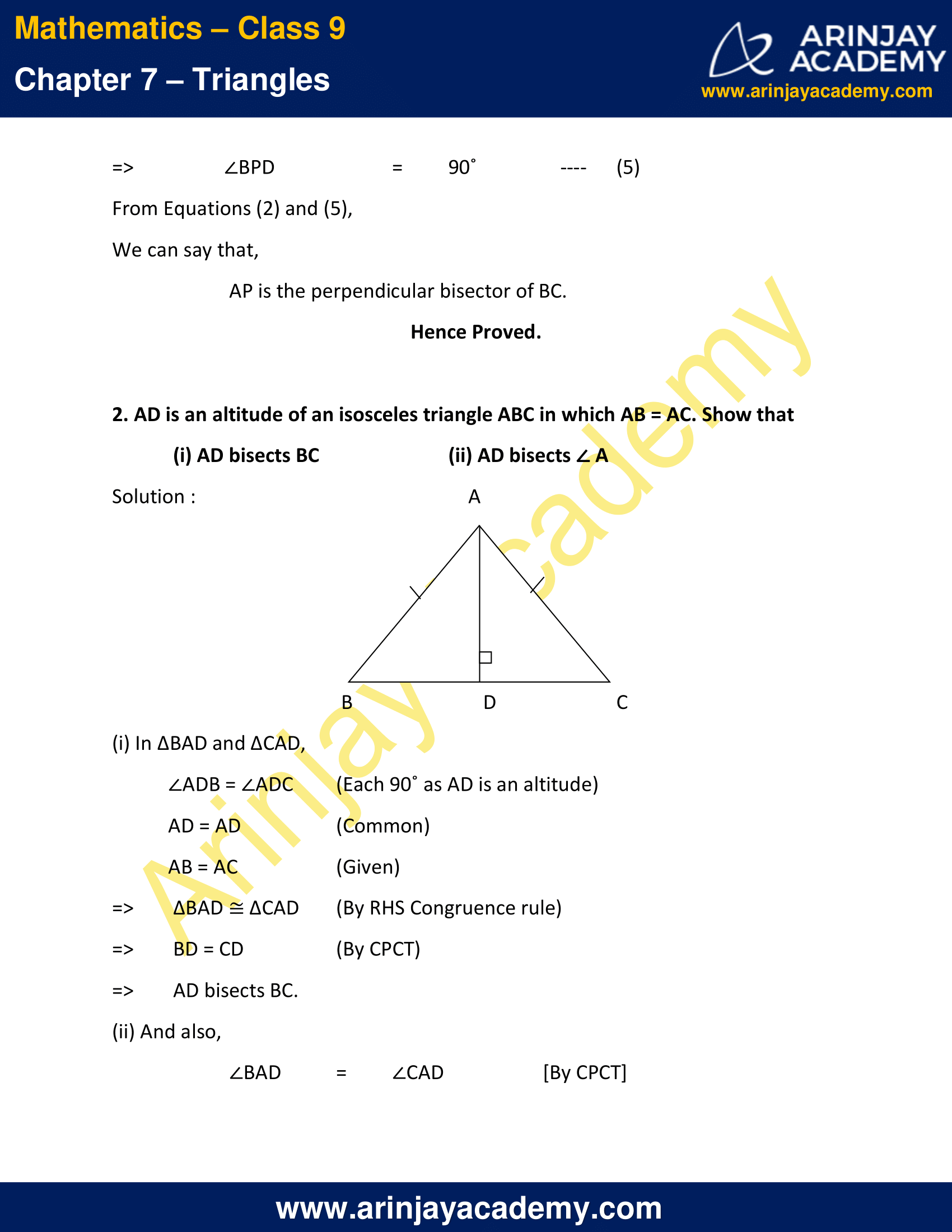
1. ∆ ABC and ∆ DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Figure). If AD is extended to intersect BC at P,
show that
(i) ∆ ABD ≅ ∆ ACD
(ii) ∆ ABP≅ ∆ ACP
(iii) AP bisects ∠ A as well as ∠ D.
(iv) AP is the perpendicular bisector of BC.
Solution :
(i) In ∆ABD and ∆ACD,
AB = AC (Given)
BD = CD (Given)
AD = AD (Common)
=> ∆ABD ≅ ∆ACD (By SSS congruence rule)
=> ∠BAD = ∠CAD (By CPCT)
=> ∠BAP = ∠CAP ..(1)
(ii) In ∆ABP and ∆ACP,
AP = AP (Common)
∠BAP = ∠CAP [From equation (1)]
AB = AC (Given)
=> ∆ABP ≅ ∆ACP (By SAS congruence rule)
=> BP = CP (By CPCT) ..(2)
(iii) From Equation (1),
∠BAP = ∠CAP
=> AP bisects ∠A.
In ∆BDP and ∆CDP,
BD = CD (Given)
DP = DP (Common)
BP = CP [From equation (2)]
=> ∆BDP ≅ ∆CDP (By SSS Congruence rule)
=> ∠BDP = ∠CDP (By CPCT) ..(3)
=> AP bisects ∠D.
(iv) ∆BDP ≅ ∆CDP
=> ∠BPD = ∠CPD (By CPCT) ..(4)
=> ∠BPD + ∠CPD = 180˚ (Since, BPC is a straight line)
=> ∠BPD + ∠BPD = 180˚
=> 2∠BPD = 180˚ [From Equation (4)]
=> ∠BPD = 90˚ …(5)
From Equations (2) and (5),
We can say that,
AP is the perpendicular bisector of BC.
Hence Proved.
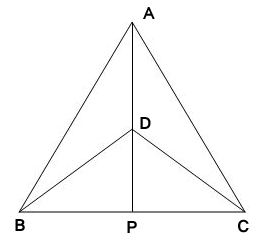
2. AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
(i) AD bisects BC
(ii) AD bisects ∠ A
Solution :
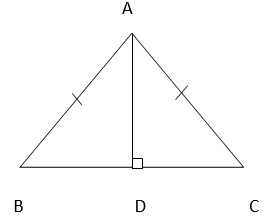
(i) In ∆BAD and ∆CAD,
∠ADB = ∠ADC (Each 90˚ as AD is an altitude)
AD = AD (Common)
AB = AC (Given)
=> ∆BAD ≅ ∆CAD (By RHS Congruence rule)
=> BD = CD (By CPCT)
=> AD bisects BC.
(ii) And also,
∠BAD = ∠CAD [By CPCT]
=> AD bisects ∠A.
Hence Proved.
3. Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ∆ PQR (see Figure). Show that:
(i) ∆ ABM ≅ ∆ PQN
(ii) ∆ ABC ≅ ∆ PQR
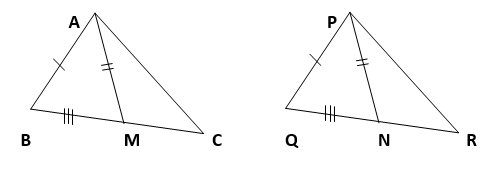
Solution :
(i) In ∆ABC,
AM is the median to BC.
=> BM = (1/2) BC
In ∆PQR,
PN is the median to QR.
=> QN = (1/2) QR
We know that,
BC = QR
=> (1/2) BC = (1/2) QR
=> BM = QN ..(1)
In ∆ABM and ∆PQN,
AB = PQ (Given)
AM = PN (Given)
BM = QN [From Equation (1)]
∆ABM ≅ ∆PQN (By SSS congruence rule)
∠ABM = ∠PQN (By CPCT)
∠ABC = ∠PQR ..(2)
(ii) In ∆ABC and ∆PQR,
AB = PQ (Given)
∠ABC = ∠PQR [From Equation (2)]
BC = QR (Given)
=> ∆ABC ≅ ∆PQR (By SAS congruence rule)
Hence Proved.
4. BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles
Solution :
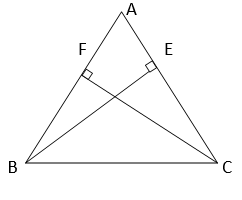
In ∆BEC and ∆CFB,
∠BEC = ∠CFB (Each 90°)
BC = CB (Common)
BE = CF (Given)
=> ∆BEC ≅ ∆CFB (By RHS congruency)
=> ∠BCE = ∠CBF (By CPCT)
=> AB = AC (Sides opposite to equal angles of a triangle are equal)
=> ∆ABC is isosceles.
Hence Proved.
5. ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC to show that ∠ B = ∠ C.
Solution :
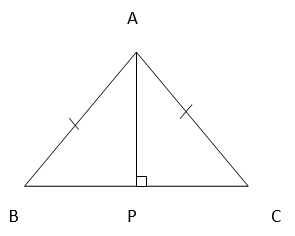
In ∆APB and ∆APC,
∠APB = ∠APC (Each 90˚)
AB =AC (Given)
AP = AP (Common)
=> ∆APB ≅ ∆APC (Using RHS congruence rule)
=> ∠B = ∠C (By using CPCT)
Hence Proved.
NCERT Solutions for Class 9 Maths Chapter 7 Exercise 7.3 – Triangles, has been designed by the NCERT to test the knowledge of the student on the following topics:-
- Some More Criteria for Congruence of Triangles
– SSS congruence rule
– RHS congruence rule
The next Exercise for NCERT Solutions for Class 9 Maths Chapter 7 Exercise 7.4 – Triangles can be accessed by clicking here.
Download NCERT Solutions for Class 9 Maths Chapter 7 Exercise 7.3 – Triangles
