NCERT Solutions for Class 9 Maths Chapter 6 Exercise 6.1 – Lines and Angles. This Exercise contains 6 questions with detailed answers. The remaining Exercise for Class 9 for Maths NCERT Solutions for Chapter 6 and Other Chapters are available at the end of this Note.
To practice Lines and Angles Class 9 Exercise 6.1, you may have to clear your concept for the Basic Terms used in Lines and Angles in Class 9. We have explained important terms, concepts, and definitions, which are used for Lines and Angles Class 9 in an interesting and easy-to-understand manner. Every effort has been made to clear every concept in a simple or easy language. To understand basic terms and definitions Click here.
NCERT Solutions for Class 9 Maths Chapter 6 Exercise 6.1 Lines and Angles


NCERT Solutions for Class 9 Maths Chapter 6 Exercise 6.1 – Lines and Angles, has been designed by the NCERT to test the knowledge of the student on the following topics:-
Important terms and Definitions for Lines and Angles Class 9
- LINE SEGMENT
Line segment is a part of line having two end points.
![]()
In the given figure, A and B are the two end points.
- RAY
Ray is a part of line having one end point.

In the given figure, A is the only end point. The Ray goes indefinitely in the other direction till infinity.
- COLLINEAR POINTS
If three or more points lie on the same line then the points are said to be collinear points.
![]()
- NON-COLLINEAR POINTS
If three of more points does not lie on the same line then the points are said to be non-collinear points.
- ANGLE
An angle is formed when two lines meets at a point.
∠CAB or ∠BAC are angle.
- ARMS
The rays making an angle are called the arms of the angle.
Here, AC and AB are arms of the angle.
- VERTEX
The point where two rays meet is called the vertex of the angle. Here, A is Vertex.
- TYPES OF ANGLES
Acute Angle:
An angle is said to be acute angle if the measure of the angle is more than 0˚ but less than 90˚.
Right Angle:
An angle is said to be right angle if the measure of the angle is 90˚.
Obtuse Angle:
An angle is said to be Obtuse angle if the measure of the angle is more than 90˚ but less than 180˚.
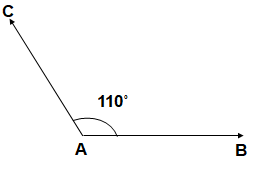
Straight Line Angle:
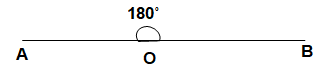
An angle is said to be straight line angle if the measure of the angle is 180˚.
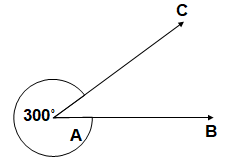
Reflex Angle:
An angle is said to be reflex angle if the measure of the angle is more than 180˚ but less than 360˚.
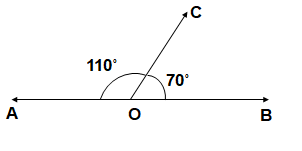
Supplementary Angles:
Two angles are said to be supplementary if the sum of their measure is 180˚.
Complementary Angles:
Two angles are said to be complementary if the sum of their measure is 90˚.
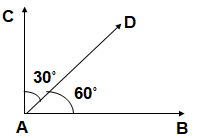
- ADJACENT ANGLES
Two angles with the same vertex, one arm common and other arm lying on opposite sides of the common arm are called adjacent angles.
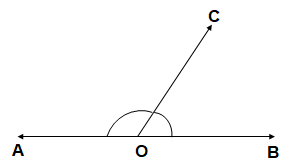
- VERTICALLY OPPOSITE ANGLES
When two lines intersect each other, then two pair of vertically opposite angles are formed.
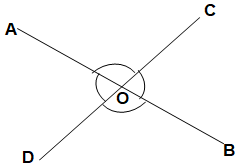
Here, line AB and BC intersect each other at point then, two pairs of vertically opposite angles formed.
(1)∠AOC and ∠BOD
(2) ∠AOD and ∠COB.
- INTERSECTING LINES AND NON-INTERSECTING LINES
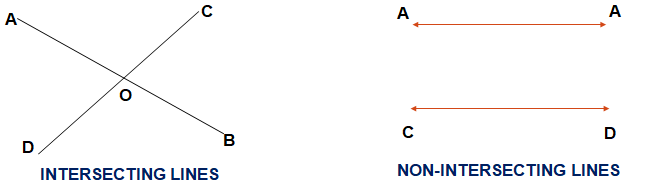
Non-intersecting lines are parallel lines because the distance between two parallel lines always remain same. So two lines are not parallel line then they must be intersecting line if they are in same plane.
The next Exercise for NCERT Solutions for Class 9 Maths Chapter 6 Exercise 6.2 – Lines and Angles can be accessed by clicking here.
NCERT Solutions for Class 9 Maths Chapter 6 Exercise 6.1 Lines and Angles
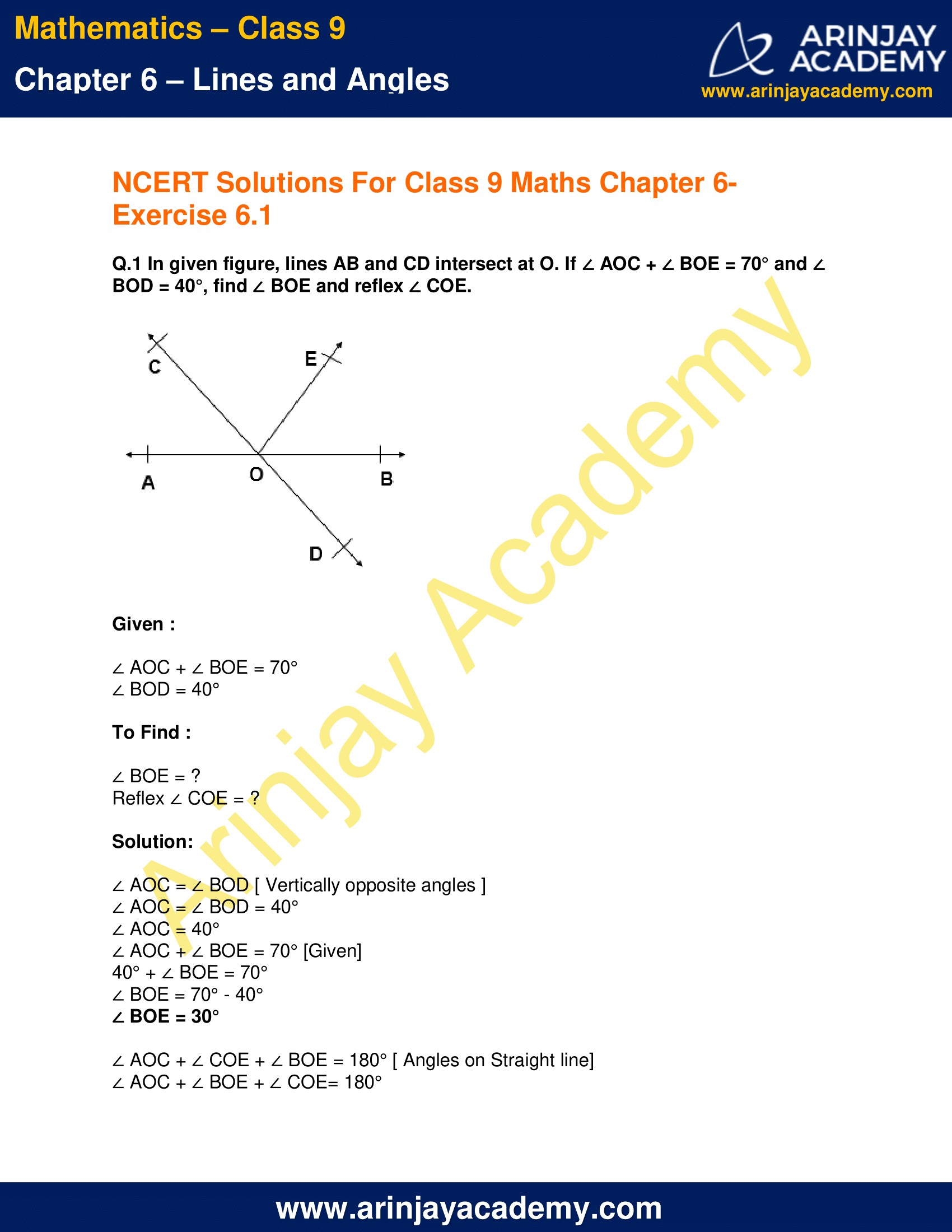
Q.1 In given figure, lines AB and CD intersect at O. If ∠ AOC + ∠ BOE = 70° and ∠ BOD = 40°, find ∠ BOE and reflex ∠ COE.
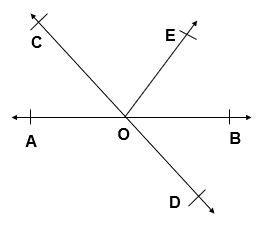
Given :
∠ AOC + ∠ BOE = 70°
∠ BOD = 40°
To Find :
∠ BOE = ?
Reflex ∠ COE = ?
Solution:
∠ AOC = ∠ BOD [ Vertically opposite angles ]
∠ AOC = ∠ BOD = 40°
∠ AOC = 40°
∠ AOC + ∠ BOE = 70° [Given]
40° + ∠ BOE = 70°
∠ BOE = 70° – 40°
∠ BOE = 30°
∠ AOC + ∠ COE + ∠ BOE = 180° [ Angles on Straight line]
∠ AOC + ∠ BOE + ∠ COE= 180°
70° ∠ COE = 180°
∠ COE = 180° – 70°
∠ COE = 110°
Reflex ∠ COE = 360° – 110°
Reflex ∠ COE = 250°
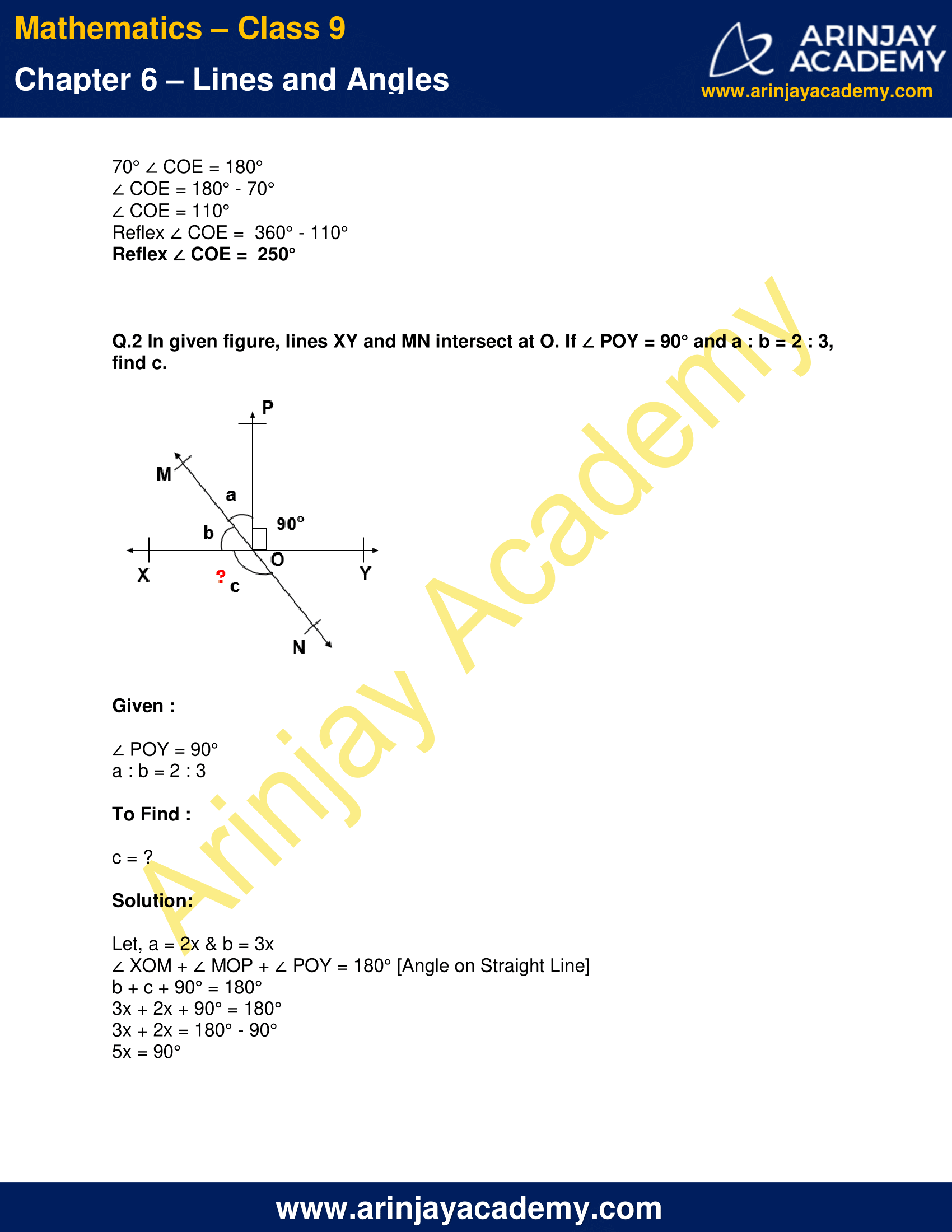
Q.2 In given figure, lines XY and MN intersect at O. If ∠ POY = 90° and a : b = 2 : 3, find c.
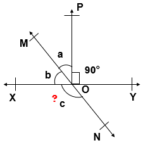
Given :
∠ POY = 90°
a : b = 2 : 3
To Find :
c = ?
Solution:
Let, a = 2x & b = 3x
∠ XOM + ∠ MOP + ∠ POY = 180° [Angle on Straight Line]
b + c + 90° = 180°
3x + 2x + 90° = 180°
3x + 2x = 180° – 90°
5x = 90°
x = (90°)/5
x = 18°
a = 2x = 2 x 18° = 36°
b = 3x = 3 x 18° = 54°
∠ XOM + ∠ XON = 180° [Linear Pair]
54° + c = 180°
c = 180° – 54°
c = 126°
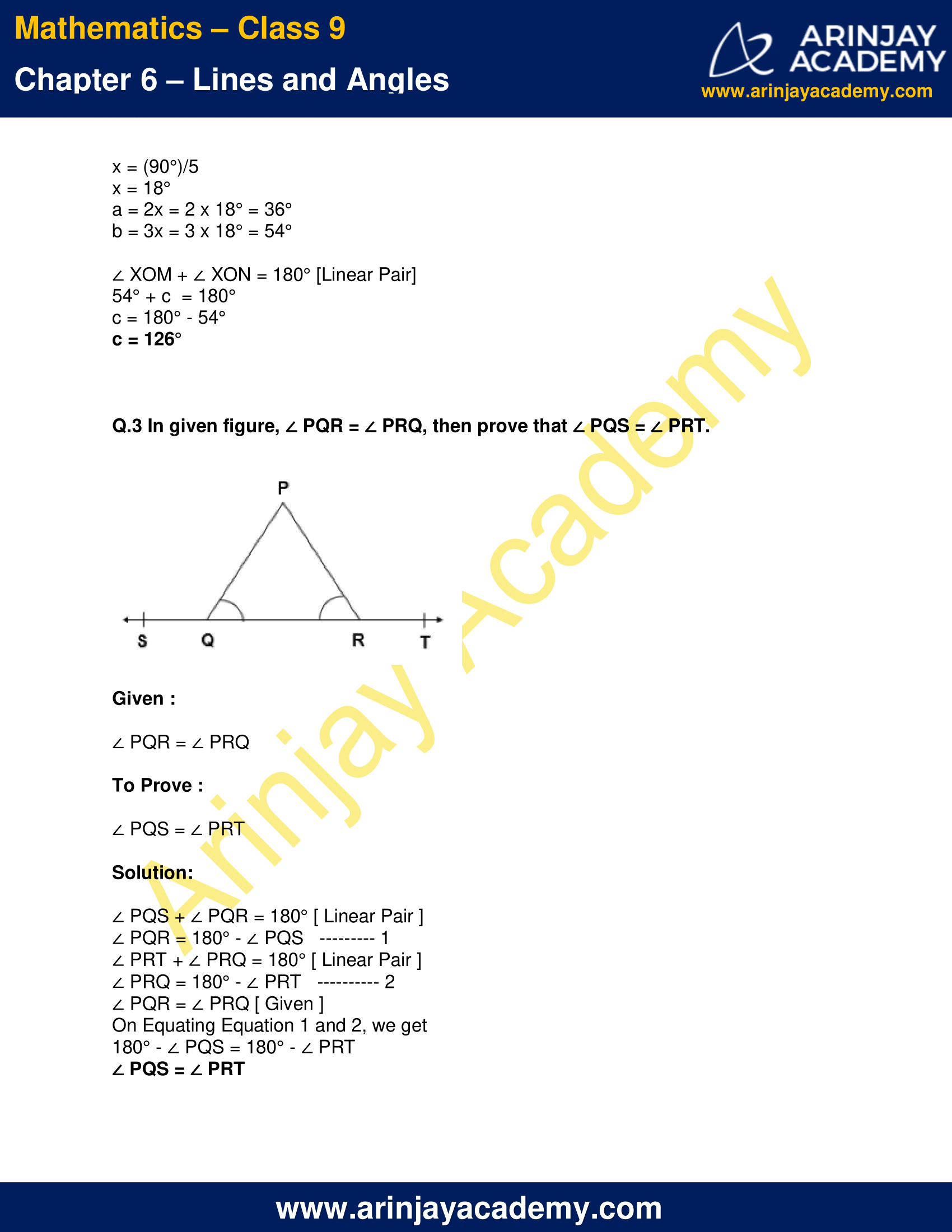
Q.3 In given figure, ∠ PQR = ∠ PRQ, then prove that ∠ PQS = ∠ PRT.
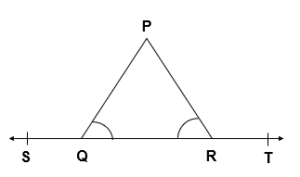
Given :
∠ PQR = ∠ PRQ
To Prove :
∠ PQS = ∠ PRT
Solution:
∠ PQS + ∠ PQR = 180° [ Linear Pair ]
∠ PQR = 180° – ∠ PQS ——— 1
∠ PRT + ∠ PRQ = 180° [ Linear Pair ]
∠ PRQ = 180° – ∠ PRT ———- 2
∠ PQR = ∠ PRQ [ Given ]
On Equating Equation 1 and 2, we get
180° – ∠ PQS = 180° – ∠ PRT
∠ PQS = ∠ PRT
Q.4 In given figure, if x + y = w + z, then prove that AOB is a line.
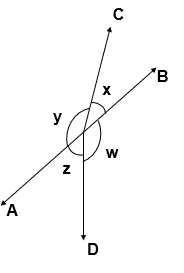
Given : x + y = w + z
To Prove : AOB is a line
Proof:
x + y + w + z = 360° [ Complete Angle ]
x + y = w + z [ Given ]
Since, x + y + x + y = 360°
2 ( x + y ) = 360°
( x + y ) = (360°)/2
( x + y ) = 180°
Since, x and y form a Linear Pair, AOB is a line
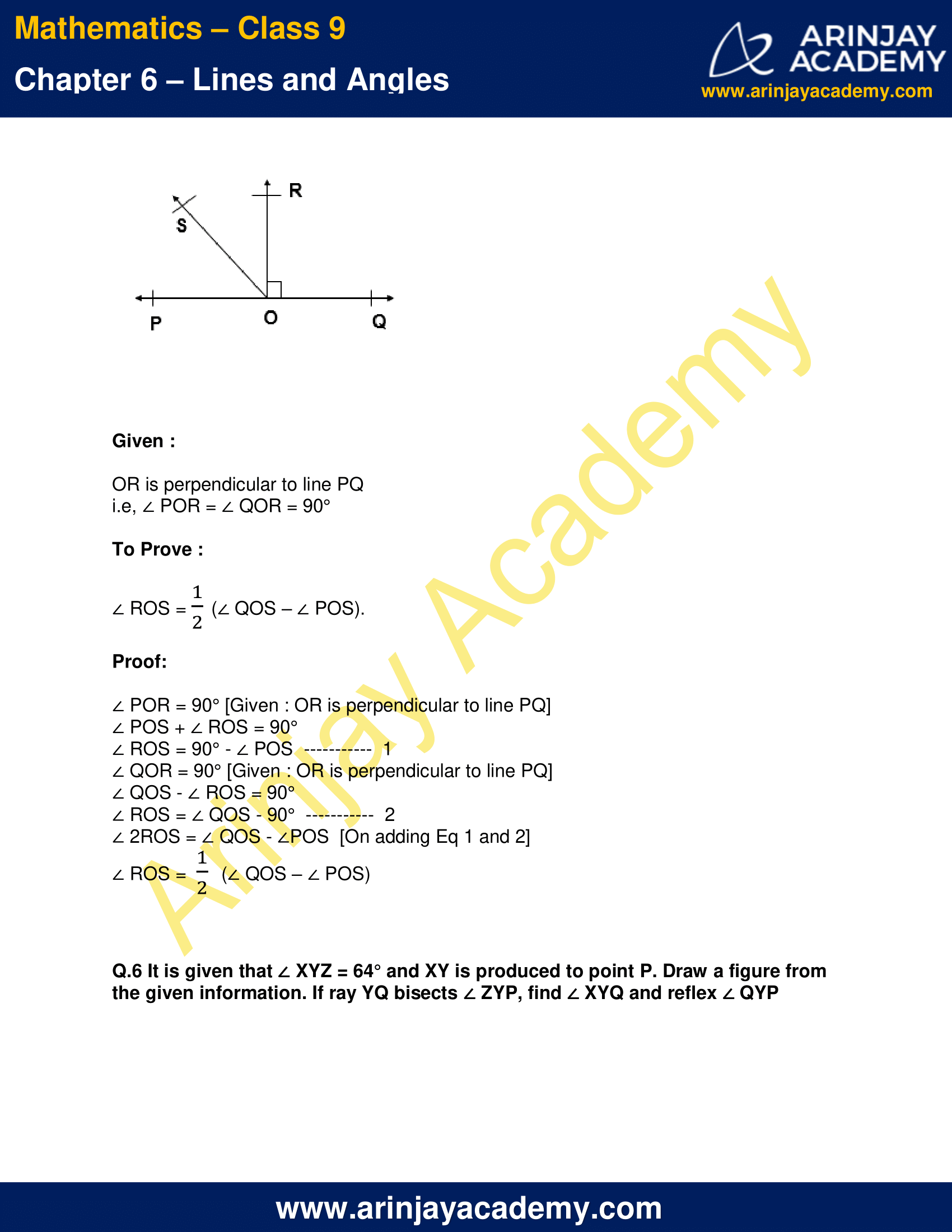
Q. 5 In given figure, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that ∠ ROS = 1/2 (∠ QOS – ∠ POS).
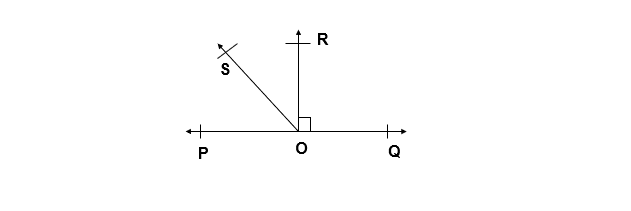
Given :
OR is perpendicular to line PQ
i.e, ∠ POR = ∠ QOR = 90°
To Prove :
∠ ROS = 1/2 (∠ QOS – ∠ POS).
Proof:
∠ POR = 90° [Given : OR is perpendicular to line PQ]
∠ POS + ∠ ROS = 90°
∠ ROS = 90° – ∠ POS ———– 1
∠ QOR = 90° [Given : OR is perpendicular to line PQ]
∠ QOS – ∠ ROS = 90°
∠ ROS = ∠ QOS – 90° ———– 2
∠ 2ROS = ∠ QOS – ∠POS [On adding Eq 1 and 2]
∠ ROS = 1/2 (∠ QOS – ∠ POS)
Q.6 It is given that ∠ XYZ = 64° and XY is produced to point P. Draw a figure from the given information. If ray YQ bisects ∠ ZYP, find ∠ XYQ and reflex ∠ QYP
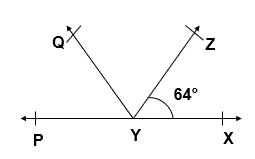
Given :
∠ XYZ = 64°
YQ bisects ∠ ZYP
i.e, ∠ ZYQ = ∠ QYP
To Find:
∠ XYQ = ?
Reflex ∠ QYP = ?
Solution:
∠ XYZ + ∠ ZYQ + QYP = 180° [Angles on a Straight line]
∠ XYZ + 2 ∠ QYP = 180° [∠ ZYQ = ∠ QYP]
64° + 2 ∠ QYP = 180°
2 ∠ QYP = 180° – 64°
2 ∠ QYP = 116°
∠ QYP = 58°
∠ ZYQ = ∠ QYP = 58°
Reflex ∠ QYP = 360° – 58° = 302°
∠ XYQ = ∠ XYZ + ∠ ZYQ
∠ XYQ = 64° + 58°
∠ XYQ = 122°
The next Exercise for NCERT Solutions for Class 9 Maths Chapter 6 Exercise 6.2 – Lines and Angles can be accessed by clicking here.
Download NCERT Solutions for Class 9 Maths Chapter 6 Exercise 6.1 – Lines and Angles
