Download NCERT Solutions for Class 9 Maths Chapter 5 Exercise 5.1 – Introduction to Euclid’s Geometry. This Exercise contains 7 questions, for which detailed answers have been provided in this note. In case you are looking at studying the remaining Exercise for Class 9 for Maths NCERT solutions for Chapter 5 or other Chapters, you can click the link at the end of this Note.
NCERT Solutions for Class 9 Maths Chapter 5 Exercise 5.1 – Introduction to Euclid’s Geometry





NCERT Solutions for Class 9 Maths Chapter 5 Exercise 5.1 – Introduction to Euclid’s Geometry
1. Which of the following statements are true and which are false? Give reasons for your answers.
(i) Only one line can pass through a single point.
(ii) There are an infinite number of lines which pass through two distinct points.
(iii) A terminated line can be produced indefinitely on both the sides.
(iv) If two circles are equal, then their radii are equal.
(v) In Fig. below, if AB = PQ and PQ = XY, then AB = XY.
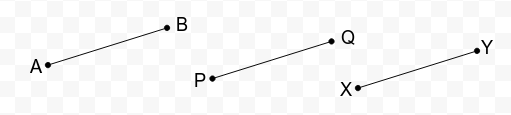
Solution :
(i) False , because one of Euclid’s Postulates state that “ A straight line may be drawn from any one point to any other point.” which concludes that there can be infinite number of line passing through a point.
(ii) False , because given two distinct points, there is a unique line that passes through them.
(iii) True , Euclid states this as a postulate as “A terminated line can be produced indefinitely.”
(iv) True , because if they are superimposed over each other , they coincide , and one of Euclid’s Axioms state that things which coincide with one another are equal to one another.
(v) True , AB = PQ and also XY = PQ and Euclid states it as “Things which are equal to the same thing are equal to one another”.
2. Give a definition for each of the following terms. Are there other terms that need to be defined first? What are they, and how might you define them?
(i) parallel lines
(ii) perpendicular lines
(iii) line segment
(iv) radius of a circle
(v) square
Solution:
(i) Parallel Lines : If two lines produced infinitely never intersect then they are called Parallel lines.
(ii) Perpendicular Lines : If two lines intersect each other at right angle, then the lines are said to be perpendicular lines.
(iii) Line Segment : The terminated line having definite length is said to be a line segment i.e. line having two endpoints.
(iv) Radius of a circle : It is the distance of any point on the circumference of a circle to the centre of the same circle.
(v) Square : A quadrilateral drawn such that all of its sides are equal and the interior angles are right angles.
Yes , there are certain terms that need to be defined first, they are as follows:
(a) Angle of intersection : It is taken as the angle between two lines at the point of their intersection.
(b) Centre of a circle : It is a point inside the circle which is equidistant from every point on its Circumference.
3. Consider two ‘postulates’ given below:
(i) Given any two distinct points A and B, there exists a third point C which is in between A and B.
(ii) There exist at least three points that are not on the same line.
Do these postulates contain any undefined terms? Are these postulates consistent?
Do they follow from Euclid’s postulates? Explain.
Solution :
Yes , They contain several undefined terms .
First of all the postulates doesn’t specify the location of the third point if it lies on the line AB or not.
Then there can be infinite number of planes passing through AB and we don’t know which plane holds the point C .
Yes , the postulates are consistent as there are infinitely many points even on a line between two distinct points and there is always a unique line passing through two points and therefore there exists at least three points that are not on the same line.
No , they do not follow Euclid’s postulates but they do follow the Axiom.
4. If a point C lies between two points A and B such that AC = BC, then prove that AC = (1/2) AB. Explain by drawing the figure.
Solution :
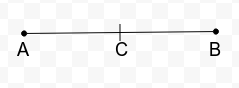
Point C lies between AB such that
AC = BC
AC + AC = AC + BC [Adding AC to both sides]
2AC = AB
AC = ½ AB
5. In Question 4, point C is called a midpoint of line segment AB. Prove that every line segment has one and only one midpoint.
Solution:
The midpoint C lies in between A and B such that AC = BC = ½ AB
Let us assume that there are more than one midpoint of a line say C and D.
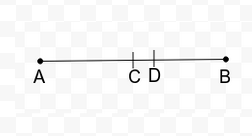
Then
AC = BC = ½ AB ….(a)
And
AD = BD = ½ AB ….(b)
Also from figure it is evident that AB = AC + CD + DB ….(c)
Substituting, AC = ½ AB and DB = ½ AB from (a) and (b) respectively we get equation (c)
AB = ½ AB + CD + ½ AB
AB = AB + CD
Which is not true .
This implies that our assumption was wrong .
Thus we conclude that every line segment has only one midpoint.
6. In Fig. below, if AC = BD, then prove that AB = CD.
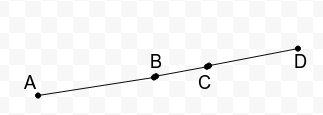
Solution:
Given that
AC = BD
Subtracting BC from both sides we get
AC – BC = BD – BC
AB = CD
[ Hence proved.]
7. Why is Axiom 5, in the list of Euclid’s axioms, considered a ‘universal truth’? (Note that the question is not about the fifth postulate.)
Solution:
Euclid’s 5th Axiom states that “The whole is greater than the part.”
Let us consider our body for example the weight of our body is something but the weight of any of our body part is always less than that of the whole body.
Therefore, it is considered a ‘universal truth’.
NCERT Solutions for Class 9 Maths Chapter 5 Exercise 5.1 – Introduction to Euclid’s Geometry, has been designed by the NCERT to test the knowledge of the student on the topic – Euclid’s Definitions, Axioms and Postulates
The next Exercise for NCERT Solutions for Class 9 Maths Chapter 5 Exercise 5.2 – Introduction to Euclid’s Geometry can be accessed by clicking here.
Download NCERT Solutions for Class 9 Maths Chapter 5 Exercise 5.1 – Introduction to Euclid’s Geometry
