Download NCERT Solutions For Class 9 Maths Chapter 2 Exercise 2.5 – Polynomials contains 16 questions, for which detailed answers have been provided in this note.
| Category | NCERT Solutions for Class 9 |
| Subject | Maths |
| Chapter | Chapter 2 |
| Exercise | Exercise 2.5 |
| Chapter Name | Polynomials |
Download NCERT Solutions for Class 9 Maths Chapter 2 Exercise 2.5 – Polynomials
NCERT Solutions for Class 9 Maths Chapter 2 Exercise 2.5 – Polynomials
1. Use suitable identities to find the following products:
(i) (x + 4) (x + 10)
(ii) (x + 8) (x – 10)
(iii) (3x + 4) (3x – 5)
(iv) [y2 + (3/2)][y2 – (3/2)]
(v) (3 – 2x) (3 + 2x)
Solution:
(i) (x + 4) (x + 10)
Using the Identity : (x + a) (x + b) = x2 + (a + b)x + ab ,
Putting a = 4 and b = 10 , we get,
(x + 4) (x + 10) = x2 + (4 + 10)x + (4)(10)
= x2 + 14x + 40
(ii) (x + 8) (x – 10)
Using the Identity : (x + a) (x + b) = x2 + (a + b)x + ab,
Putting a = 8 and b = – 10 , we get,
(x + 8) (x – 10) = x2 + (8 – 10)x + (8)(-10)
= x2 – 2x – 80
(iii) (3x + 4) (3x – 5)
Using the Identity : (x + a) (x + b) = x2 + (a + b)x + ab,
Applying the above identity, we get,
(3x + 4) (3x – 5) = (3x)2 + (4 – 5)(3x) + (4)(-5)
= 9x2 – 3x – 20
(iv) [y2 + (3/2)][y2 – (3/2)]
Using the Identity : (x + a) (x + b) = x2 + (a + b)x + ab,
Applying the above identity, we get,
[y2 + (3/2)][y2 – (3/2)] = (y2)2 + [(3/2) – 93/2)](3x) + (3/2)(-3/2)
= y4 – (9/4)
(v) (3 – 2x) (3 + 2x)
Using the Identity : (x + y) (x – y) = x2 – y2,
Applying the above identity , we get,
(3 – 2x) (3 + 2x) = (3)2 – (2x)2
= 9 – 4x2
2. Evaluate the following products without multiplying directly:
(i) 103 × 107
(ii) 95 × 96
(iii) 104 × 96
Solution:
(i) 103 × 107 = (100 + 3) x (100 + 7)
= 1002 + (3 + 7)(100) + (3)(7) [Use : (x + a) (x + b) = x2 + (a + b)x + ab]
= 10000 + 1000 + 21
= 11021
(ii) 95 × 96 = (100 – 5 ) x (100 – 4)
= 1002 + (- 5 – 4)(100) + (-5)(-4) [Use : (x + a) (x + b) = x2 + (a + b)x + ab ]
= 10000 – 900 + 20
= 9120
(iii) 104 × 96 = (100 + 4 ) x (100 – 4)
= 1002 + ( 4 – 4)(100) + (4)(-4) [Use : (x + a) (x + b) = x2 + (a + b)x + ab ]
= 10000 – 16
= 9984
Download NCERT Solutions for Class 9 Maths Chapter 2 Exercise 2.5 – Polynomials
3. Factorise the following using appropriate identities:
(i) 9x2 + 6xy + y2
(ii) 4y2 – 4y + 1
(iii) x2 – y2/100
Solution:
(i) 9x2 + 6xy + y2 = (3x)2 + 2(3x)(y) + (y)2 [Use : x2 + 2xy + y2 = (x + y)2]
= (3x + y)2
= (3x + y)(3x + y)
(ii) 4y2 – 4y + 1 = (2y)2 – 2(2y)(1) + (1)2 [Use : x2 – 2xy + y2 = (x – y)2]
= (2y – 1)2
= (2y – 1)(2y – 1)
(iii) x2 – y2/100 = x2 – (y/10)2 [ Use : x2 – y2 = (x + y) (x – y) ]
= (x + y/10) (x – y/10)
4. Expand each of the following, using suitable identities:
(i) (x + 2y + 4z)2
(ii) (2x – y + z)2
(iii) (–2x + 3y + 2z)2
(iv) (3a – 7b – c)2
(v) (–2x + 5y – 3z)2
(vi) [a/4 – b/2 + 1]2
Solution:
Using the identity (x + y + z)2 = x2 + y2 + z2 + 2xy + 2yz + 2zx
We can substitute the given terms with corresponding values of x , y , z and expand as follows:
(i) (x + 2y + 4z)2 = (x)2 + (2y)2 + (4z)2 + 2(x)(2y) + 2(2y)(4z) + 2(4z)(x)
= x2 + 4y2 + 16z2 + 4xy + 16yz + 8zx
(ii) (2x – y + z)2 = (2x)2 + (-y)2 + (z)2 + 2(2x)(-y) + 2(-y)(z) + 2(z)(2x)
= 4x2 + y2 + z2 – 4xy – 2yz + 4zx
(iii) (–2x + 3y + 2z)2= (-2x)2 + (3y)2 + (2z)2 + 2(-2x)(3y) + 2(3y)(2z) + 2(2z)(-2x)
= 4x2 + 9y2 + 4z2 – 12xy + 12yz – 8zx
(iv) (3a – 7b – c)2 = (3a)2 + (-7b)2 + (-c)2 + 2(3a)(-7b) + 2(-7b)(-c) + 2(-c)(3a)
= 9a2 + 49b2 + c2 – 42ab + 14bc – 6ca
(v) (–2x + 5y – 3z)2 = (-2x)2 + (5y)2 + (-3z)2 + 2(-2x)(5y) + 2(5y)(-3z) + 2(-3z)(-2x)
= 4x2 + 25y2 + 9z2 – 20xy – 30yz + 12zx
(vi) [a/4 – b/2 + 1]2 = (a/4)2 + (-b/2)2 + (1)2 + 2(a/4)(-b/2) + 2(-b/2)(1) + 2(1)(a/4)
= a2/16 + b2/4 + 1 – ab/4 – b + a/2
5. Factorise:
(i) 4x2 + 9y2 + 16z2 + 12xy – 24yz – 16xz
(ii) 2x2 + y2 + 8z2 – 2 xy + 4 yz – 8xz
Solution:
(i)Given
4x2 + 9y2 + 16z2 + 12xy – 24yz – 16xz = (2x)2+(3y)2+(-4z)2+2(2x)(3y)+2(3y)(-4z) +2(2x)(-4z)
Using Identity: x2 + y2 + z2 + 2xy + 2yz + 2zx = (x + y + z)2 we get
4x2 + 9y2 + 16z2 + 12xy – 24yz – 16xz = (2x + 3y – 4z)2
= (2x + 3y – 4z)(2x + 3y – 4z)
(ii) Given
2x2 + y2 + 8z2 – 2 xy + 4 yz – 8xz = ( x)2 + y2 + (2 z)2 + 2 x)(y) + 2(y)(2 z) + 2(- x)(2 z)
Using Identity: x2 + y2 + z2 + 2xy + 2yz + 2zx = (x + y + z)2 we get
2x2 + y2 + 8z2 – 2 xy + 4 yz – 8xz = ( x + y + 2 z)2
= ( x + y + 2 z)( x + y + 2 z)
6. Write the following cubes in expanded form:
(i) (2x + 1)3
(ii) (2a – 3b)3
(iii) (3x/2 + 1)3
(iv) ( x – 2y/3)3
Solution:
Using the identities (x + y)3 = x3 + y3 + 3xy (x + y) ….(1)
And (x – y)3 = x3 – y3 – 3xy(x – y) ….(2)
We can substitute the given terms with corresponding values of x , y and expand as follows:
(i) (2x + 1)3
Using identity (1) we have
(2x + 1)3 = (2x)3 + 13 + 3(2x)(1)(2x + 1)
= 8x3 + 1 + 12x2 + 6x
(ii) (2a – 3b)3
Using identity (2) we have
(2a – 3b)3 = (2a)3 – (3b)3 – 3(2a)(3b)(2a – 3b)
= 8a3 – 27b3 – 36a2b + 54ab2
(iii) (3x/2 + 1)3
Using identity (1) we have
(3x/2 + 1)3 = (3x/2)3 + 13 + 3(3x/2)(1)(3x/2 + 1)
= 27x3/8 + 1 + 27x2/4 + 9x/2
(iv) ( x – 2y/3)3
Using identity (2) we have
( x – 2y/3)3 = (x)3 – (2y/3)3 – 3(x)(2y/3)(x – 2y/3)
= x3 – 8y3/27 – 2x2y + 4xy2/3
7. Evaluate the following using suitable identities:
(i) (99)3
(ii) (102)3
(iii) (998)3
Solution:
(i) We have (99)3 = (100 – 1)3
Using identity (x – y)3 = x3 – y3 – 3xy(x – y) we get
(100 – 1)3 = 1003 – 13 – 3(100)(1)(100 – 1)
= 1000000 – 1 – 29700
= 970299
(ii) We have (102)3 = (100 + 2)
Using the identity (x + y)3 = x3 + y3 + 3xy (x + y) we get
(100 + 2)3 = 1003 + 23 + 3(100)(2)(100 + 2)
= 1000000 + 8 + 61200
= 1061208
(iii) We have (998)3 = (1000 – 2)3
Using identity (x – y)3 = x3 – y3 – 3xy(x – y) we get
(1000 – 2)3 = 10003 – 23 – 3(1000)(2)(1000 – 2)
= 1000000000 – 8 – 5988000
= 994011992
8. Factorise each of the following:
(i) 8a3 + b3 + 12a2b + 6ab2
(ii) 8a3 – b3 – 12a2b + 6ab2
(iii) 27 – 125a3 – 135a + 225a2
(iv) 64a3 – 27b3 – 144a2b + 108ab2
(v) 27p3 – 1/216 – (9/2)p2 + p/4
Solution:
We know the identities :
(1) (x + y)3 = x3 + y3 + 3xy (x + y)
= x3 + y3 + 3x2y + 3xy2
Therefore,
x3 + y3 + 3x2y + 3xy2 = (x + y)3
(2) (x – y)3 = x3 – y3 – 3xy(x – y)
= x3 – 3x2y + 3xy2 – y3
Therefore,
x3 – 3x2y + 3xy2 – y3 = (x – y)3
(i) We have 8a3 + b3 + 12a2b + 6ab2
= (2a)3 + b3 + 3(2a)2b + 3(2a)b2
Comparing it with identity (1) we get
8a3 + b3 + 12a2b + 6ab2 = (2a + b)3
= (2a + b)(2a + b)(2a + b)
(ii) We have 8a3 – b3 – 12a2b + 6ab2
= (2a)3 – b3 – 3(2a)2b + 3(2a)b2
Comparing it with identity (2) we get
8a3 – b3 – 12a2b + 6ab2 = (2a – b)3
= (2a – b)(2a – b)(2a – b)
(iii) We have 27 – 125a3 – 135a + 225a2
= 33 – (5a)3 – 3(32)(5a) + 3(3)(5a)2
Comparing it with identity (2) we get
27 – 125a3 – 135a + 225a2 = (3 – 5a)3
= (3 – 5a)(3 – 5a)(3 – 5a)
(iv) We have 64a3 – 27b3 – 144a2b + 108ab2
= (4a)3 – (3b)3 – 3(4a)2(3b) + 3(4a)(3b)2
Comparing it with identity (2) we get
64a3 – 27b3 – 144a2b + 108ab2 = (4a – 3b)3
= (4a – 3b)(4a – 3b)(4a – 3b)
(v) We have 27p3 – 1/216 – (9/2)p2 + p/4
= (3p)3 – (1/6)3 – 3(3p)2(1/6) + 3(3p)(1/6)2
Comparing it with identity (2) we get
27p3 – 1/216 – (9/2)p2 + p/4= (3p – 1/6)3
= (3p – 1/6)(3p – 1/6)(3p – 1/6)
Download NCERT Solutions for Class 9 Maths Chapter 2 Exercise 2.5 – Polynomials
9. Verify : (i) x3 + y3 = (x + y) (x2 – xy + y2 ) (ii) x3 – y3 = (x – y) (x2 + xy + y2 )
Solution :
(i) We have x3 + y3 = (x + y) (x2 – xy + y2 )
Using identity : (x + y)3 = x3 + y3 + 3xy (x + y)
For given problem
L.H.S. = x3 + y3 = (x + y)3 – 3xy (x + y)
Taking (x + y ) common
= (x + y)((x + y)2 – 3xy)
Using identity : (x + y)2 = x2 + 2xy + y2
L.H.S = x3 + y3 = (x + y)(x2 + 2xy + y2 – 3xy)
= (x + y)(x2 – xy + y2) = R.H.S.
(ii) x3 – y3 = (x – y) (x2 + xy + y2 )
Using identity : (x – y)3 = x3 – y3 – 3xy(x – y)
For given problem
L.H.S. = x3 – y3 = (x – y)3 + 3xy (x – y)
Taking (x – y ) common
= (x – y)((x – y)2 + 3xy)
Using identity : (x – y)2 = x2 – 2xy + y2
L.H.S = x3 – y3 = (x – y)(x2 – 2xy + y2 +3xy)
= (x – y)(x2 + xy + y2) = R.H.S.
10. Factorise each of the following:
(i) 27y3 + 125z3
(ii) 64m3 – 343n3
Solution :
Using the results of previous question i.e.
x3 + y3 = (x + y) (x2 – xy + y2 ) …..(1)
x3 – y3 = (x – y) (x2 + xy + y2 ) …..(2)
We can solve the given problems as follows
(i) 27y3 + 125z3
Using equation (1) we get ,
27y3 + 125z3 = (3y)3 + (5z)3 = (3y + 5z) (9y2 – 15yz + 25z2 )
(ii) 64m3 – 343n3
Using equation (2) we get ,
64m3 – 343n3 = (4m)3 + (7n)3 = (4m – 7n) (16m2 + 28mn + 49n2)
11. Factorise : 27x3 + y3 + z3 – 9xyz
Solution:
Using the identity x3 + y3 + z3 – 3xyz = (x + y + z)(x2 + y2 + z2 – xy – yz – zx)
We can substitute the given terms with corresponding values of x , y , z and expand as follows:
27x3 + y3 + z3 – 9xyz = (3x)3 + y3 + z3 – 3(3x)yz
= (3x + y + z)(9x2 + y2 + z2 – 3xy – yz – 3zx)
12. Verify that x3 + y3 + z3 -3xyz = (½)( x + y + z ) [ ( x − y )2 + ( y − z )2 + ( z − x )2 ]
Solution:
Using the identity x3 + y3 + z3 – 3xyz = (x + y + z)(x2 + y2 + z2 – xy – yz – zx)
We have L.H.S. = x3 + y3 + z3 – 3xyz = (x + y + z)(x2 + y2 + z2 – xy – yz – zx)
[Multiplying and dividing by 2]
= (½)(x + y + z)(2x2 + 2y2 + 2z2 – 2xy – 2yz – 2zx)
Rearranging the terms as follows :
= (½)(x + y + z)(x2 + y2 – 2xy + y2 + z2– 2yz + x2+ z2 – 2zx)
Using the identity: (x – y)2 = x2 – 2xy + y2
= (½)( x + y + z ) [ ( x − y )2 + ( y − z )2 + ( z − x )2 ]
= R.H.S.
13. If x + y + z = 0, show that x3 + y3 + z3 = 3xyz.
Solution :
We know the identity x3 + y3 + z3 – 3xyz = (x + y + z)(x2 + y2 + z2 – xy – yz – zx)
Putting x + y + z = 0 we get
x3 + y3 + z3 – 3xyz = (0)(x2 + y2 + z2 – xy – yz – zx) = 0
Or, x3 + y3 + z3 = 3xyz.
14. Without actually calculating the cubes, find the value of each of the following:
(i) (–12)3 + (7)3 + (5)3
(ii) (28)3 + (–15)3 + (–13)3
Solution :
Using the results obtained in the previous question we know that ,
If, x + y + z = 0
Then, x3 + y3 + z3 = 3xyz.
Using this result we can find the required values as follows :
(i) We have (–12)3 + (7)3 + (5)3
Since, (–12) + (7) + (5) = 0
Therefore, (–12)3 + (7)3 + (5)3 = 3(-12)(7)(5) = -1260
(ii) We have (28)3 + (–15)3 + (–13)3
Since, (28) + (–15) + (–13) = 0
Therefore, (28)3 + (–15)3 + (–13)3= 3(28)(-15)(-13) = 16380
15. Give possible expressions for the length and breadth of each of the following rectangles, in which their areas are given:
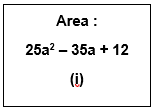

Solution:
(i) Given Area = 25a2 – 35a + 12
Splitting the middle term we get
25a2 – 35a + 12 = 25a2 – 20a – 15a + 12
= 5a(5a – 4) – 3(5a – 4)
= (5a – 4)(5a – 3) [Taking (5a-4) common]
Also, area of a rectangle is given by (length)(breadth)
Comparing it with the above expression we get
Possible dimensions of the length and breadth as (5a – 4) and (5a – 3).
(ii) Given Area = 35y2 + 13y –12
Splitting the middle term we get
35y2 + 13y –12 = 35y2 + 28y – 15y –12
= 7y(5y + 4) – 3(5y + 4)
= (5y + 4)(7y – 3) [Taking (5a-4) common]
Also , area of a rectangle is given by (length)(breadth)
Comparing it with the above expression we get
Possible dimensions of the length and breadth as (5y + 4) and (7y – 3).
16. What are the possible expressions for the dimensions of the cuboids whose volumes are given below?
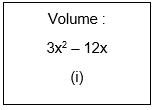

Solution:
(i) Given volume = 3x2 – 12x
= 3x(x – 4) [Taking 3x common]
Also , volume of a cuboid is given by (length)(breadth)(height)
Comparing it with the above expression we get
Possible dimensions of the cuboid as 3 , x , and (x – 4).
(ii) Given volume = 12ky2 + 8ky – 20k
= k(12y2 + 8y – 20) [Taking k common]
= k(12y2 + 20y – 12y – 20) [ Splitting the middle term]
= k(4y(3y + 5) – 4(3y + 5)) [Taking (3y + 5) common]
= k(4y – 4)(3y + 5)
Also , volume of a cuboid is given by (length)(breadth)(height)
Comparing it with the above expression we get
Possible dimensions of the cuboid as k , (4y – 4) , and (3y + 5).
NCERT Solutions for Class 9 Maths Chapter 2 Exercise 2.5 – Polynomials, has been designed by the NCERT to test the knowledge of the student on the topic – Algebraic Identities
The next Exercise for NCERT Solutions for Class 9 Maths Chapter 3 Exercise 3.1 – Coordinate Geometry can be accessed by clicking here.