Download NCERT Solutions For Class 9 Maths Chapter 2 Exercise 2.3 – Polynomials contains 3 questions, for which detailed answers have been provided in this note.
| Category | NCERT Solutions for Class 9 |
| Subject | Maths |
| Chapter | Chapter 2 |
| Exercise | Exercise 2.3 |
| Chapter Name | Polynomials |
Download NCERT Solutions for Class 9 Maths Chapter 2 Exercise 2.3 – Polynomials
NCERT Solutions for Class 9 Maths Chapter 2 Exercise 2.3 – Polynomials
1.Find the remainder when x3 + 3x2 + 3x + 1 is divided by
(i) x + 1
(ii) x – ½
(iii) x
(iv) x + π
(v) 5 + 2x
Solution:
According to remainder theorem if polynomial p(x) of greater than or equal to one is divided by the linear polynomial (x – a) , then the remainder is p(a) where a is any real number.
Here, p(x) = x3 + 3x2 + 3x + 1
(i) Given linear polynomial is (x + 1) , having zero equal to -1.
Putting x= -1 in p(x) , we get
p(-1) = (-1)3 + 3(-1)2 + 3(-1) + 1
= -1 + 3 – 3 + 1
= 0
So , by remainder theorem , remainder in this case is 0.
Alternative Method – We can also use long division method as follows :
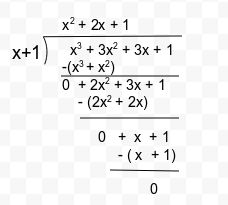
Thus, we conclude that the remainder is zero in this case.
(ii) Given linear polynomial is (x – ½ ) , having zero equal to ½ .
Putting x= ½ in p(x) , we get
p(½ ) = (½ )3 + 3(½ )2 + 3(½ ) + 1
= ⅛ + ¾ + 3/2 + 1
= (1 + 6 + 12 + 8)/8
= 27/8
So , by remainder theorem , remainder in this case is 27/8 .
Alternative Method – We can also use long division method as follows :
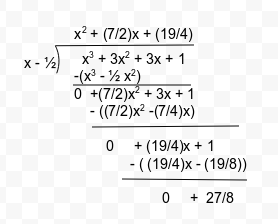
Thus, we conclude that the remainder is (27/8) in this case.
(iii) Given linear polynomial is (x + 0) , having zero equal to 0.
Putting x= 0 in p(x) , we get
p(0) = (0)3 + 3(0)2 + 3(0) + 1
= 0 + 0 + 0 + 1
= 1
So , by remainder theorem , remainder in this case is 1.
Alternative Method – We can also use long division method as follows :
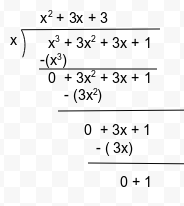
Thus, we conclude that the remainder is 1 in this case.
(iv)Given linear polynomial is (x + π ) , having zero equal to -π .
Putting x= -π in p(x) , we get
p(-π ) = (-π )3 + 3(-π )2 + 3(-π ) + 1
= – π3 + 3π2 – 3π + 1
So , by remainder theorem , remainder in this case is (- π3 + 3π2 – 3π + 1).
Alternative Method – We can also use long division method as follows :
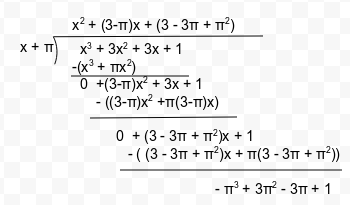
Thus, we conclude that the remainder is (- π3 + 3π2 – 3π + 1) in this case.
Download NCERT Solutions for Class 9 Maths Chapter 2 Exercise 2.3 – Polynomials
(v) 5 + 2x
Given linear polynomial is (5 + 2x) , having zero equal to -5/2 .
Putting x= -5/2 in p(x) , we get
p(-5/2 ) = (-5/2)3 + 3(-5/2)2 + 3(-5/2) + 1
= -(125/8) + (75/4) -(15/2) + 1
= (-125 + 150 – 60 + 8)/8
= -(27/8)
So , by remainder theorem , remainder in this case is -(27/8).
Alternative Method – We can also use long division method as follows :
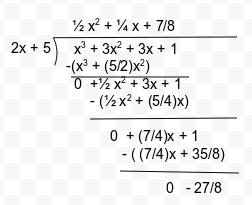
Thus, we conclude that the remainder is -(27/8) in this case.
2. Find the remainder when x3 – ax2 + 6x – a is divided by x – a.
Solution:
Given
p(x) = x3 – ax2 + 6x – a
And the linear polynomial is (x – a) , having zero equal to a.
Putting x= a in p(x) , we get
p(a) = a3 – a(a)2 + 6a – a
= a3 – a3 + 6a – a
= 5a
According to remainder theorem if polynomial p(x) of greater than or equal to one is divided by the linear polynomial (x – a) , then the remainder is p(a) where a is any real number.
So , by remainder theorem , remainder in this case is 5a.
3. Check whether 7 + 3x is a factor of 3x3 + 7x.
Solution:
We know that 7 + 3x is a factor of 3x3 + 7x , only if on division by 7 + 3x , 3x3 + 7x doesn’t leave any remainder .
And, According to remainder theorem if polynomial p(x) of greater than or equal to one is divided by the linear polynomial (x – a) , then the remainder is p(a) where a is any real number.
Here we have
p(x) = 3x3 + 7x
And the linear polynomial is (7 + 3x) , having zero equal to (-7/3).
Putting x= -7/3 in p(x) , we get
p(-7/3) = 3(-7/3)3 + 7(-7/3)
= (-343 – 147 ) / 9
= – 490/9
So , by remainder theorem , remainder in this case is -490/9.
Therefore, we conclude that 7 + 3x is not a factor of 3x3 + 7x because the remainder is not zero.
NCERT Solutions for Class 9 Maths Chapter 2 Exercise 2.3 – Polynomials, has been designed by the NCERT to test the knowledge of the student on the topic – Remainder Theorem
The next Exercise for NCERT Solutions for Class 9 Maths Chapter 2 Exercise 2.4 – Number System can be accessed by clicking here.