NCERT Solutions For Class 9 Maths Chapter 12 Exercise 12.2 – Heron’s Formula

Download NCERT Solutions For Class 9 Maths Chapter 12 Exercise 12.2 – Heron’s Formula. This Exercise contains 9 questions, for which detailed answers have been provided in this note. In case you are looking at studying the remaining Exercise for Class 9 for Maths NCERT solutions for other Chapters, you can click the link at the end of this Note.

NCERT Solutions For Class 9 Maths Chapter 12 Exercise 12.2 – Heron’s Formula

NCERT Solutions For Class 9 Maths Chapter 12 Exercise 12.2 – Heron’s Formula

1. A park, in the shape of a quadrilateral ABCD, has ∠ C = 90°, AB = 9 m, BC = 12 m, CD = 5 m and AD = 8 m. How much area does it occupy?

Solution  :

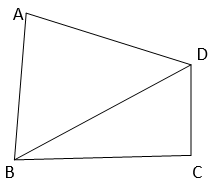
Given,
ABCD is a quadrilateral having ∠ C = 90°, AB = 9 m, BC = 12 m, CD = 5 m and AD = 8 m.
Construction : Join BD.
In ∆BCD, using Pythagoras theorem
BC² + CD² = BD²
=> (12)² + (5)² = BD²
=> BD² = 144  +  25
=> BD² = 169
=> BD = 13 m   ….(1)
Area of the ∆ BCD
= 1/2 x ( base ) x ( height )
= 1/2 x ( BC ) x ( CD )
= 1/2 x (12) x (5)
=> Area of the ∆BCD = 30 m²   …. (2)
From the triangle ABD,
AB  =  9 m (given)
AD  =  8 m (given)
BD  =  13 m ( from(1) )
Semi-perimeter of the triangle ABD,
s = (9+8+13/2)
s = 15 m
Area of the triangle ABD
=  √[s (s-a) (s-b) (s-c) ]
=  √(15) (15-9) (15-8) (15-13)
=  √(15) (6) (7) (2)
=  6√35 m² — (3)
Area of the quadrilateral ABCD
= ar (∆ ABD) + ar (∆ BCD)
= [ 6√35 + 30 ] m² ( From (1) & (2) )

2. Find the area of a quadrilateral ABCD in which AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm.

Solution :

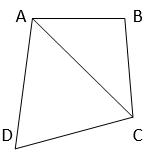
Given,  ABCD is a quadrilateral and AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm
In triangle ABC
AB  =  3 cm
BC  =  4 cm
AC  =  5 cm
Semi-perimeter,
s = (3+4+5/2)
s = 6 cm
Area of the ∆ = √s (s-a) (s-b) (s-c)
= √(6) (6-3) (6-4) (6-5)
= √(6) (3) (2) (1)
= √36
=> Area of the ∆ABC  = 6 cm²   … (1)
In triangle ADC,
AD  =  5 cm
DC  =  4 cm
AC  =  5 cm
Semi-perimeter,
s = (5+4+5/2)
s = 7 cm
Area of the ∆ADC
= √s (s-a) (s-b) (s-c)
= √(7) (7-5) (7-4) (7-5)
= √(7) (2) (3) (2)
=> Area of the ∆ADC = 2√21 cm²  …. (2)
Area of the quadrilateral ABCD
= ar (∆ ABC ) + ar (∆ ADC)
= [ 6  +  2√21 ] cm² ( from (1) & (2)  )

3. Radha made a picture of an aeroplane with coloured paper as shown in Figure Find the total area of the paper used.

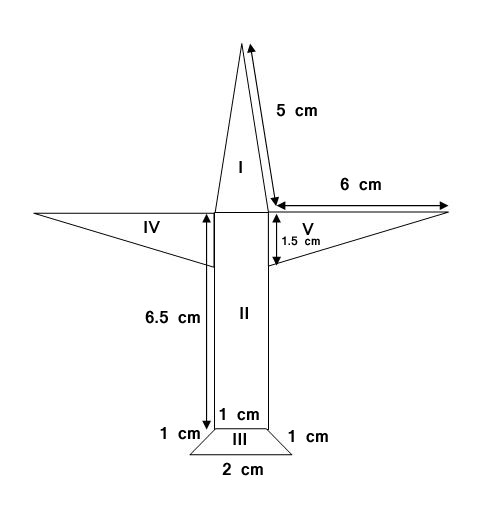
Solution :

Part I :   

       

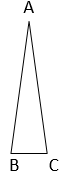
Here, AB  =  AC  =  5 cm  &  BC = 1 cm
Semi-perimeter
s = (5+5+1/2)
s = 5.5 cm
Area of the triangle ABC
= √s (s-a) (s-b) (s-c)
= √(5.5) (5.5-5) (5.5-5) (5.5-1)
= √(5.5) (0.5) (0.5) (4.5)
= (0.5) (0.5)3√11
= 0.75√11 cm²
=> Area of  Part I = 2.488 cm² ( approximately )
Part II :
Area of the rectangle = ( length ) x ( breadth )
= (6.5)  x (1)
= 6.5 cm²
=> Area of Part II = 6.5 cm²
Part III :

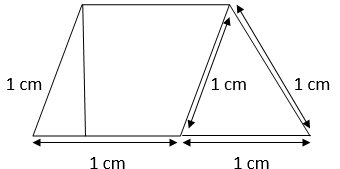
Area of the Trapezium
= Area of the parallelogram + Area of the equilateral triangle
Area of the parallelogram = (base) x (height)
Height of the parallelogram = Height of the equilateral triangle
= (√3)/2 ( 1 cm)
( Since, the height of equilateral triangle with side length ‘a’  =  [ (√3)/2 ] (a)  )
= (√3)/2 cm
Area of the parallelogram = (√3)/2 x (1)
= (√3)/2 cm²
Area of the equilateral triangle with side length ‘a’ = [(√3)/4] (a²)
=> Area of the equilateral triangle = [(√3)/4] (1²)
= [(√3)/4] cm²
Area of the trapezium
=  Area of the parallelogram  +  Area of the equilateral triangle
= [(√3)/2] + [(√3)/4] cm²
=>       Area of Part III =  1.299 cm²     ( approximately )
Area of Part IV = Area of Part V = A₄₅ ( say )
A₄₅ = Area of a right angled triangle with base (1.5 cm) and height (6 cm)
= 1/2 x ( base ) x ( height )
= 1/2 x ( 1.5 ) x ( 6)
=  4.5 cm²
=> Area of Part IV = 4.5 cm²
=> Area of Part V = 4.5 cm²
Total area of the paper used
= Area of ( Part I  +  Part II  +  Part III  +  Part IV  +  Part V )
= 6.5  +  2.488  +  1.299  +  4.5  +  4.5
= 19.287 cm²

4. A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are 26 cm, 28 cm and 30 cm, and the parallelogram stands on the base 28 cm, find the height of the parallelogram.

Solution :

Given
Sides of the triangle are 26 cm, 28 cm and 30 cm.
Semi-perimeter,
s  =  (26+28+30/2)
s  =  42 cm
Area of triangle
= √s (s-a) (s-b) (s-c)
= √(42) (42-26) (42-28) (42-30)
= √(42) (16) ( 14) ( 12)
= 336 cm²
=> Area of the triangle = 336 cm²
=> Area of the parallelogram = 336 cm²
We know that,
Area of the parallelogram = ( base ) x ( height )
336 = ( 28 ) x ( height )
=>  height = 336/28
= 12 cm
=> Height of the parallelogram = 12 cm

5. A rhombus shaped field has green grass for 18 cows to graze. If each side of the rhombus is 30 m and its longer diagonal is 48 m, how much area of grass field will each cow be getting?

Solution : 

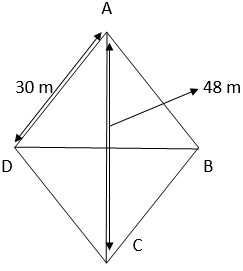
Area of the rhombus ABCD = Area of the triangle ABC + Area of the triangle ADC
For triangle ABC,
AB = 30 m
BC = 30 m
AC = 48 m
Semi-perimeter,
s  =  (30+30+48/2)
s  =  54 m
Area of the triangle ABC = √s (s-a) (s-b) (s-c)
= √(54) (54-30) (54-30) (50-48)
= √(54) (24) (24) (12)
= √3 x 6 x 24
= √432 m²
In rhombus ABCD,
Area of the triangle ABC = Area of the triangle ADC
=> Area of the rhombus ABCD = 2 x (Area of the triangle ABC )
= 2 x 432
= 864 m²
Area for gazing for 1 cow
= 864/18
= 48 m²

6. An umbrella is made by stitching 10 triangular pieces of cloth of two different colours (see Figure), each piece measuring 20 cm, 50 cm and 50 cm. How much cloth of each colour is required for the umbrella?

                       

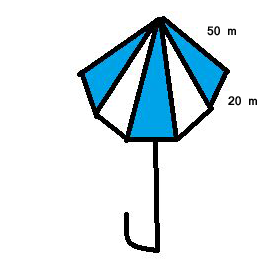
Solution :

Area of each triangular cloth = √ [s (s-a) (s-b) (s-c) ]
s = (20+50+50/2)
= 60 cm
Area = √(60) (60-50) (60-50) (60-20)
= √(60) (10) (10) (40)
= 200√6 cm²
Since there are 5 triangular pieces made of two different colour cloths,
Area of each colour cloth = 5 x 200√6
= 1000√6 cm²

7. A kite in the shape of a square with a diagonal 32 cm and an isosceles triangle of base 8 cm and sides 6 cm each is to be made of three different shades as shown in Figure. How much paper of each shade has been used in it?

                           

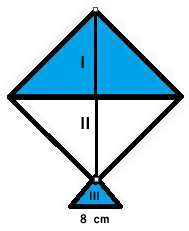
Solution :

We know that,
Area of a square = 1/2 (Length of the diagonal)²
= 1/2 (32)²
Area of the kite = 512 cm²
Area of Part I = Area of Part II = (Area of kite)/2
Area of Part I = Area of Part II = 256 cm²
Area required for each shade = 256 cm²
Part III
Area of the triangle = √ [s (s-a) (s-b) (s-c) ]
s = (8+6+6)/2
= 10 cm
Area of the triangle = √(10) (10-6) (10-8) (10-6)
= √(10) (4) (2) (4)
= 8√5 cm²
Area of Part III  = 8√5 cm²

8. A floral design on a floor is made up of 16 tiles which are triangular, the sides of the triangle being 9 cm, 28 cm and 35 cm (see Figure). Find the cost of polishing the tiles at the rate of 50p per cm² .

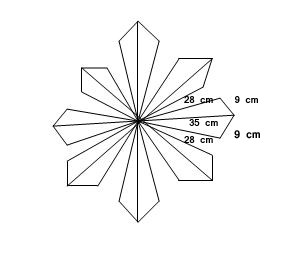
Solution :
Area of triangle = √[s (s-a) (s-b) (s-c)]
s = (28+35+9)/2
= 36 cm
Area of each tile = √(36) (36-28) (36-35) (36-9)
= √(36) (8) (1) (27)
= 36 √6  cm²
Area of 16 tiles = 16 x 36 √ 6
= 576 √6 cm²
Cost of polishing per cm² area = 50 p
Cost of polishing per 576√6 cm²  area = 50p x 576√6
= Rs. 288√6
=> It will cost Rs. 705.45 for polishing all tiles.

 9. A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m. The non-parallel sides are 14 m and 13 m. Find the area of the field.

Solution :

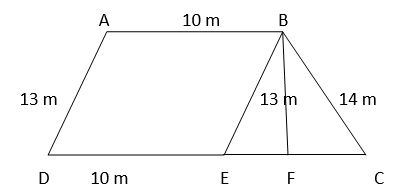
Given, ABCD is a trapezium.
Construction :
Draw a line from B which is parallel to AD and let it intersect CD at E
Since, CD  =  25 m & DE  =  10 m
=> EC = CD – DE
=  25 – 10 = 15 m
From the triangle BEC,
s = (13+14+15)/2
= 21 m
Area of the triangle BEC
= √[s (s-a) (s-b) (s-c) ]
= √(21) (21-13) (21-14) (21-15)
=  √(21) (8) (7) (6)
=  √84 m²
We know that,
Area of the triangle = (1/2) x ( base ) x ( height )
84 = (1/2) x ( 15 ) x ( BF )
=> BF =11.2 m
Area of parallelogram = ( base) x ( height )
= ( DE ) x ( BF )
= (10) x (11.2)
= 112 m²
Area of the field = 84  +  112
= 196 m²

NCERT Solutions for Class 9 Maths Chapter 12 Exercise 12.2 – Heron’s Formula, has been designed by the NCERT to test the knowledge of the student on the topic – Application of Heron’s Formula in Finding Areas of Quadrilaterals

• Maths – NCERT Solutions Class 9
• NCERT Solutions Class 9

Download NCERT Solutions For Class 9 Maths Chapter 12 Exercise 12.2 – Heron’s Formula