NCERT Solutions for Class 9 Maths Chapter 10 Exercise 10.5 – Circles

Download NCERT Solutions for Class 9 Maths Chapter 10 Exercise 10.5 – Circles. This Exercise contains 12 questions, for which detailed answers have been provided in this note. In case you are looking at studying the remaining Exercise for Class 9 for Maths NCERT solutions for other Chapters, you can click the link at the end of this Note.

NCERT Solutions for Class 9 Maths Chapter 10 Exercise 10.5 – Circles

NCERT Solutions for Class 9 Maths Chapter 10 Exercise 10.5 – Circles

1. In given figure, A,B and C are three points on a circle with centre O such that ∠ BOC = 30° and ∠ AOB = 60°. If D is a point on the circle other than the arc ABC, find ∠ADC.

                   

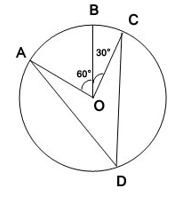
Solution :

Here, it can be clearly observed that
∠AOC = ∠AOB + ∠BOC
= 60°  +  30°
= 90°
We know that,
The angle subtended by an arc at the centre is double the angle subtended by it any point on the remaining part of the circle.
=> ∠ADC = (1/2) ∠ AOC
=>  ∠ADC =  (1/2) x 90°
=>  ∠ADC = 45°

2. A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.

Solution :

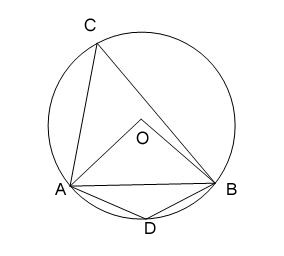
In ∆ AOB,
AB  =  OA  =  OB  ( Given )
=> ∆ AOB is an equilateral triangle.
=> ∠ AOB = ∠ OAB = ∠ OBA = 60°
And that implies, ∠ ACB =  (1/2) ∠ AOB = 30°
Here, ADBC is a cyclic quadrilateral.
=> ∠ ACB  +  ∠ ADB = 180°
=> ∠ ADB = 180°  –  30°
=> ∠ ADB = 150°
Hence, the angle subtended by this chord at a point on the major arc and the minor arc are 30° and 150° respectively.

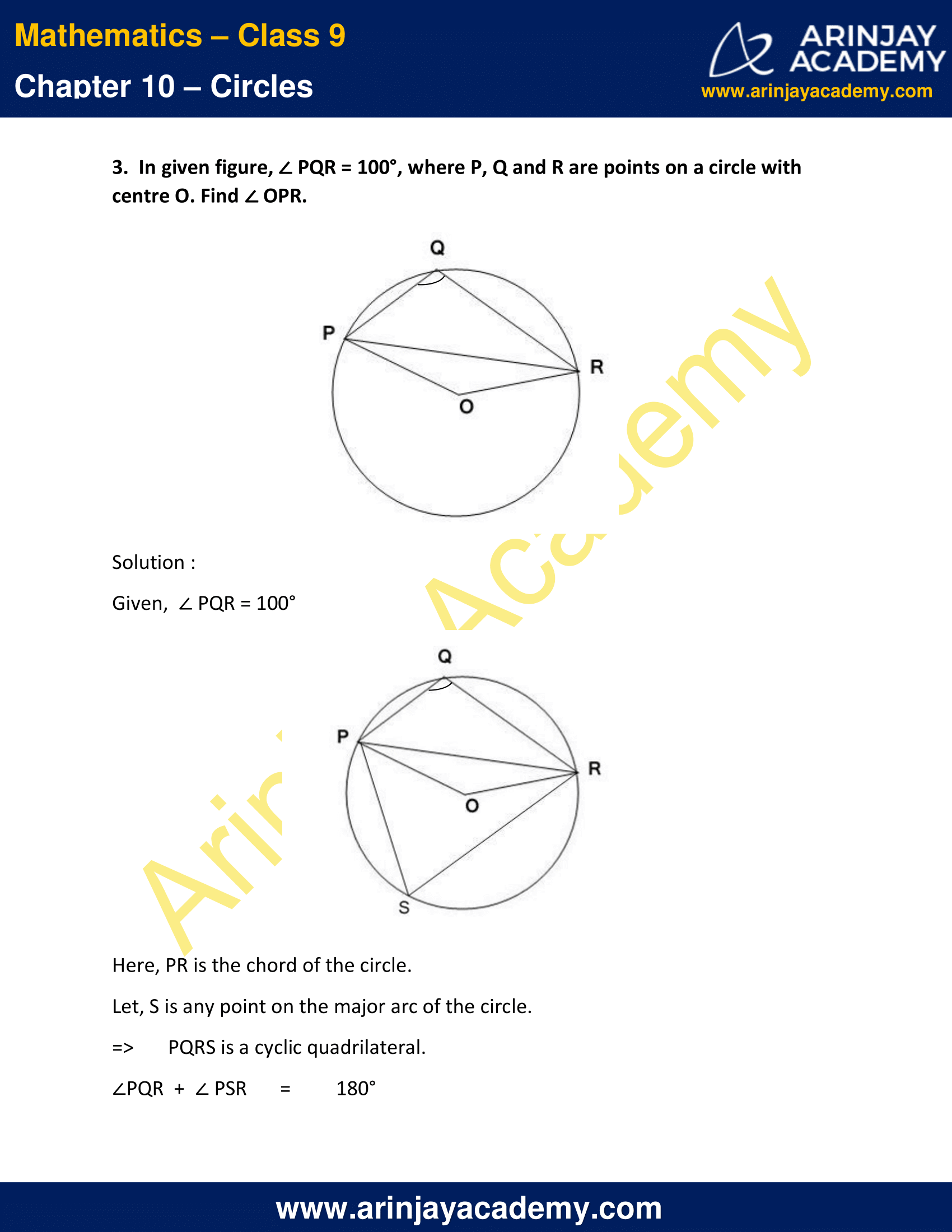
3. In given figure, ∠ PQR = 100°, where P, Q and R are points on a circle with centre O. Find ∠ OPR.

                            

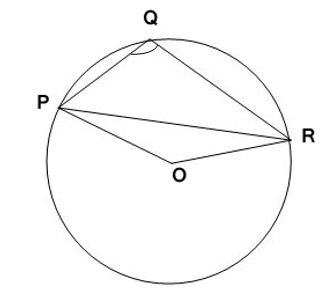
Solution :

Given,  ∠ PQR = 100°

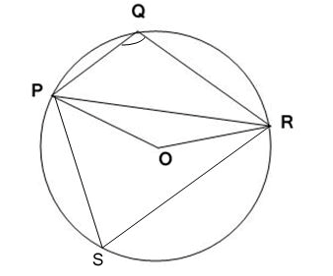
Here, PR is the chord of the circle.
Let, S is any point on the major arc of the circle.
=> PQRS is a cyclic quadrilateral.
∠PQR  +  ∠ PSR = 180°
=> ∠ PSR = 180°  – 100°
=> ∠ PSR = 80°
We know that,
The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
=>  ∠ POR = 2 (∠ PSR )
= 2 x 80°
= 160°
In triangle POR,
OP  =  OR ( Both are Radii )
=> ∠ PRO  =  ∠ OPR
∠ POR  +  ∠ PRO  +  ∠ OPR = 180°
=> 2 ∠ OPR = 180°  –  160°
=> 2 ∠ OPR = 20°
=> ∠ OPR = 10°

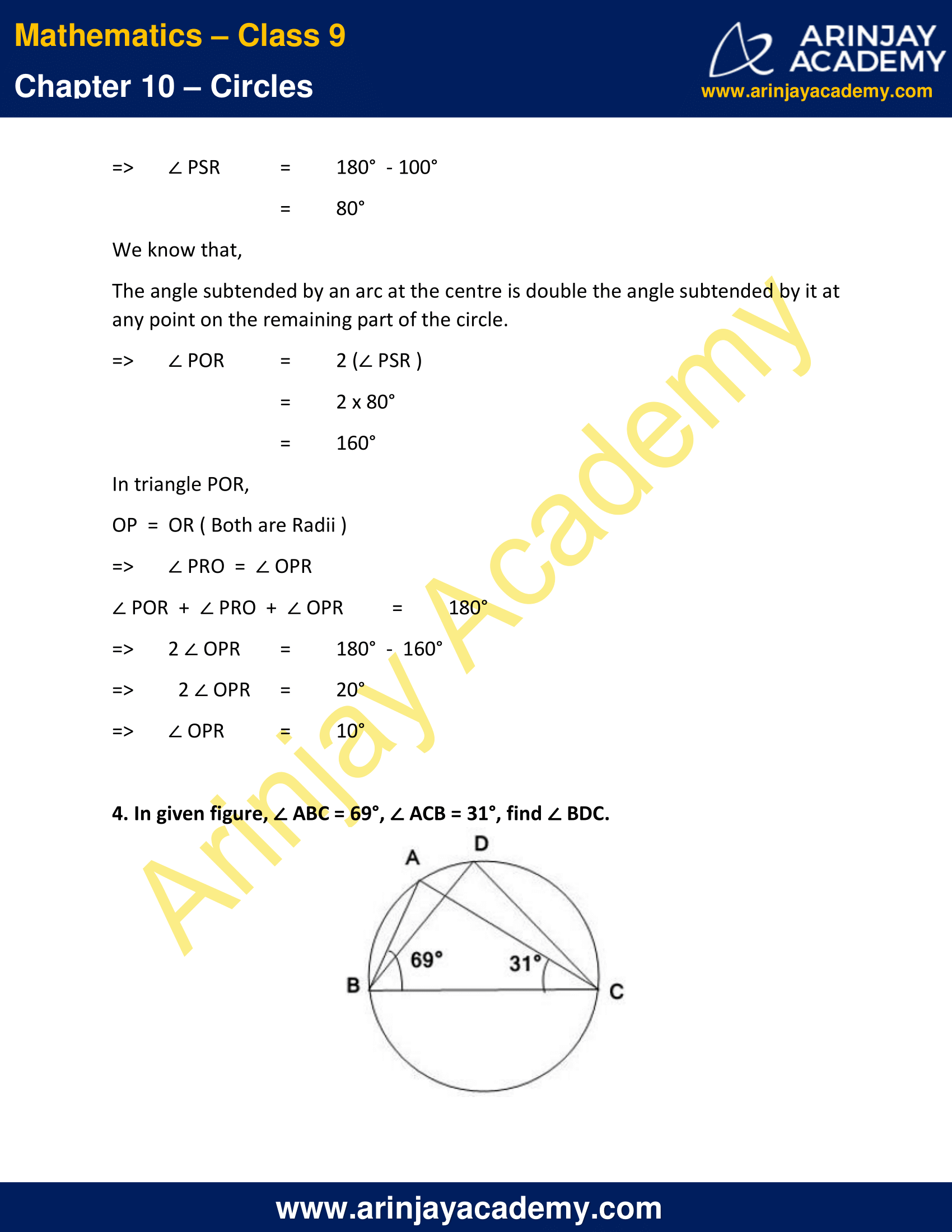
4. In given figure, ∠ ABC = 69°, ∠ ACB = 31°, find ∠ BDC.

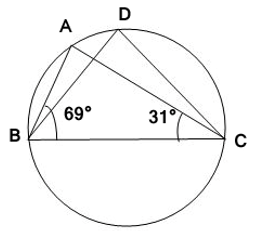
Solution :

We know that,
Angles subtend by same chord in same segment will be equal.
=> ∠ BAC = ∠ BDC   ..(1)
In triangle ABC,
∠ BAC + ∠ ABC + ∠ ACB = 180°
=> ∠ BAC  +  69°  +  31° = 180°
=> ∠ BAC = 180°  –  100°
=> ∠ BAC = 80°
From (1)
∠ BDC =  80°

5. In given figure, A, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠ BEC = 130° and ∠ ECD = 20°. Find ∠ BAC.

                           

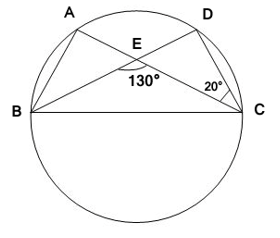
Solution :

Since, BED is a straight line
∠ BEC  +  ∠ CED = 180°
=> ∠ CED = 180°  –  130°
=> ∠ CED = 50°
From the triangle EDC,
∠ EDC + ∠ CED + ∠ ECD = 180°
=> ∠ EDC = 180°  –  50°  –  20°
=> ∠ EDC = 110°
We know that,
∠ EDC = ∠ BDC
=> ∠ BDC = 110°
We know that,
Angles in same segment make by same chord will be equal.
=> ∠ BDC = ∠ BAC
=> ∠ BAC  = 110°

6. ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠ DBC = 70°, ∠ BAC is 30°, find ∠ BCD. Further, if AB = BC, find ∠ ECD.

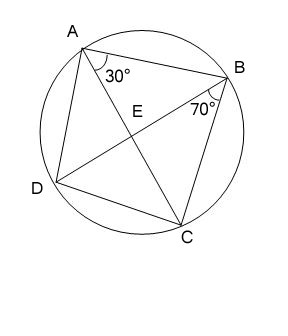
Solution :

We know that,
Angles in the same segment form by same chord will be equal.
For chord CD,
∠CBD = ∠CAD
=> ∠CAD    =   70°
∠BAD = ∠CAD + ∠CAB
= 70°   +   30°
= 100°
Since ABCD is a cyclic quadrilateral,
∠BAD + ∠BCD = 180°
∠BCD = 180°  –  100°
∠BCD = 80°  ..(1)
In the triangle ABC,
AB  =  BC  ( given )
=> ∠BCA = ∠BAC
=  30°
∠BCD = ∠BCA + ∠ACD
=> ∠ ACD = 80°  –  30°
=> ∠ ACD = 50°
We know that,
∠ ACD = ∠ ECD
=> ∠ ECD = 50°

7. If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.

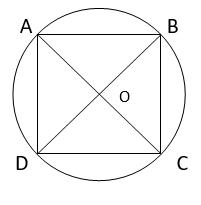
Solution :

Here, ABCD is a cyclic quadrilateral intersecting their diagonals AC & BD at center of the circle O.
Consider the chord BD,
=> ∠BAD = (1/2) ∠BOD
=> ∠BAD = (1/2) ( 180°)
=> ∠BAD = 90°
In a cyclic quadrilateral ABCD,
∠BAD  +  ∠BCD = 180°
=> ∠BCD = 180°  –  90°
=> ∠BCD = 90°
Consider the chord AC,
=> ∠ABC = (1/2) ∠AOC
=> ∠ABC = (1/2) ( 180°)
=> ∠ABC = 90°
In a cyclic quadrilateral ABCD,
∠ABC  +  ∠ADC = 180°
=> ∠ADC = 180°  –  90°
=> ∠ADC = 90°
Each interior angle of the cyclic quadrilateral is 90°.
=> Cyclic quadrilateral having diameters of the circle as its diagonals will be a rectangle.

Hence Proved.

8. If the non-parallel sides of a trapezium are equal, prove that it is cyclic.

Solution :

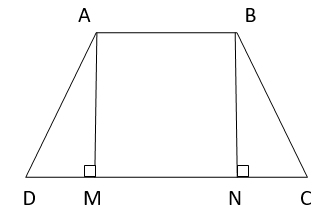
Here, ABCD is a trapezium with AB || CD.
AD   =   BC  ( Given )
Construction :
Draw perpendiculars from A & B on CD.
=> AM  &  BN  are perpendicular to CD.
From the triangles AMD  &  BNC,
∠AMD = ∠BNC  (Each 90˚)
AM  =  BN  ( Perpendicular distance between parallel lines will be equal )
AD  =  BC  ( given )
=> ∆ AMD  &  ∆ BNC are congruent under R.H.S. congruency rule.
=> ∠ADC  =  ∠BCD  [By CPCT]  ..(1)
( Corresponding angles are equal in congruent triangles )
AB  || CD
AD is the transversal.
∠BAD  + ∠ADC = 180°
From  (1),
∠BAD  + ∠BCD = 180° ..(2)
∠ABC  +  ∠ADC  + ∠BAD  +  ∠BCD  = 360°
=> ∠ABC  +  ∠ADC = 180°   ..(3)
Equation (2) & Equation (3) shows that the opposite angles are supplementary.
We can say that,
If the non-parallel sides of a trapezium are equal, then it will be cyclic.
Hence Proved.

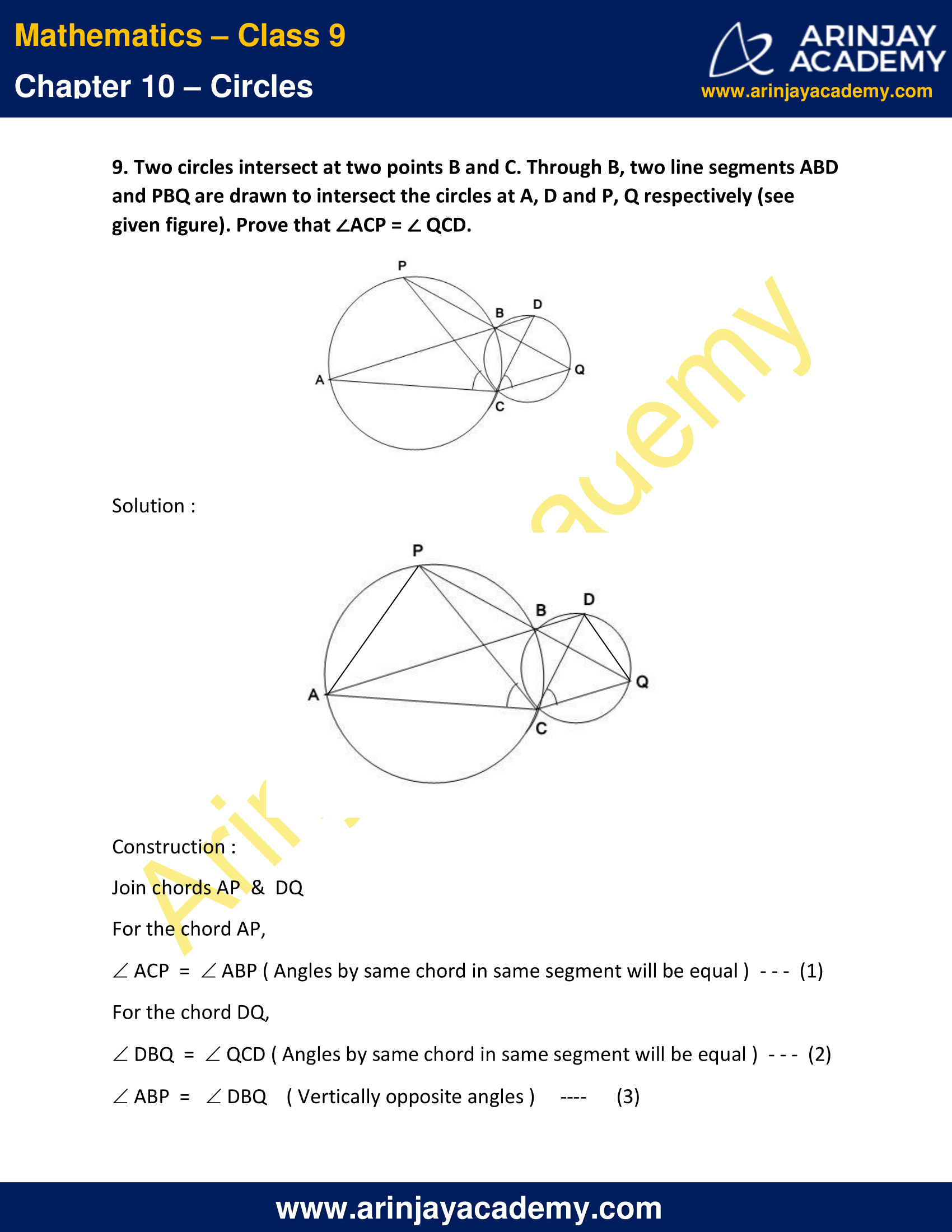
9. Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see given figure). Prove that ∠ACP = ∠ QCD.

                               

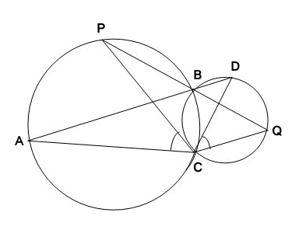
Solution :

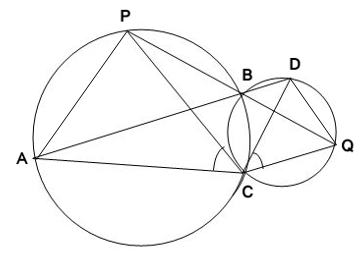
Construction :
Join chords AP  &  DQ
For the chord AP,
∠ACP  =  ∠ABP ( Angles by same chord in same segment will be equal )  ..(1)
For the chord DQ,
∠DBQ  =  ∠QCD ( Angles by same chord in same segment will be equal )  ..(2)
∠ABP  =  ∠DBQ    ( Vertically opposite angles )  ..(3)
From (1), (2) & (3),
We can say that,
∠ACP = ∠ QCD
Hence Proved.

10. If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.

Solution :

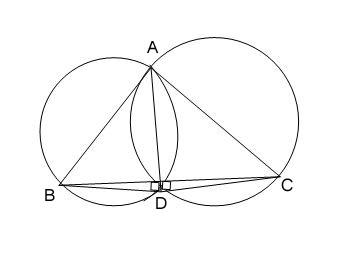
Consider the triangle ABC.
Here AB & AC are diameters of the respective circles.
Those two circles intersect at A & D
D do not lie on BC.
=> ∠ADB  =  ∠ADC  =  90°   ( Angle in a semi-circle is 90°)
We know that,
∠BDC = ∠ADB  + ∠ADC
= 90° + 90°
= 180°
=> Therefore, BDC is a straight line (D should lie on the line BC)
=> Hence, our assumption was wrong
=> The intersecting point of circles should lie on the third side of the triangle.
Hence Proved.

11. ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠ CAD = ∠ CBD.

Solution :

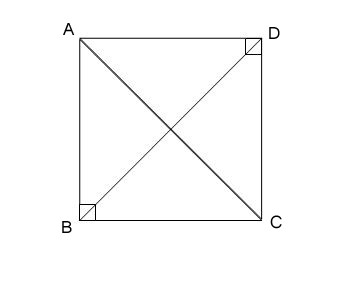
From the triangle ABC,
∠ABC  +  ∠BAC  +  ∠ACB = 180° ( sum of interior angle in a triangle is 180°)
90°  +  ∠BAC  +  ∠ACB = 180°
=> ∠BAC  +  ∠ACB = 90°  ..(1)
From the triangle ADC,
∠ADC  +  ∠DAC  + ∠ACD = 180° ( sum of interior angle in a triangle is 180°)
90°  +  ∠DAC  +  ∠ACD = 180°
=> ∠DAC  + ∠ACD = 90°  ..(2)
Adding the equations (1) & (2),
=> ∠BAC  + ∠ACB  + ∠DAC  + ∠ACD = 90° +  90°
=  180°
=> (∠BAC  + ∠DAC)   +  (∠ACB  + ∠ACD) = 180°
=> ∠BAD +  ∠BCD = 180°  ..(3)
We have,
∠ABC  + ∠ADC  =  180° ..(4)
From (3) & (4),
We can say that, ABCD is a cyclic quadrilateral.

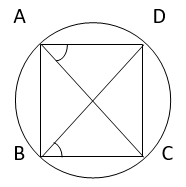
Here it can be clearly see that
∠ CAD = ∠ CBD   ( Angles in same segment by same chord will be equal. )

Hence Proved.

12. Prove that a cyclic parallelogram is a rectangle.

Solution :

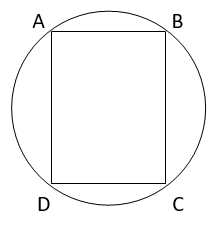
Here ABCD is a cyclic parallelogram.
∠ DAB  +  ∠ DCB  = 180°   .. (1)
And we know that,
In a parallelogram opposite angles are equal.
=>∠ DAB  =  ∠ DCB   .. (2)
From (1) & (2)
∠ DAB  =  ∠ DCB   =   90°
Parallelogram will be a rectangle if one of its interior angle is 90°.
Hence, cyclic parallelogram is a rectangle.

NCERT Solutions for Class 9 Maths Chapter 10 Exercise 10.5 – Circles, has been designed by the NCERT to test the knowledge of the student on the following topics:-

• Angle Subtended by an Arc of a Circle
• Cyclic Quadrilaterals

 

• Maths – NCERT Solutions Class 9
• NCERT Solutions Class 9

Download NCERT Solutions for Class 9 Maths Chapter 10 Exercise 10.5 – Circles