Download NCERT Solutions For Class 9 Maths Chapter 1 Exercise 1.5 – Number System. This Exercise contains 5 questions, for which detailed answers have been provided in this note. In case you are looking at studying the remaining Exercise for Class 9 for Maths NCERT solutions for Chapter 1 or other Chapters, you can click the link at the end of this Note.
NCERT Solutions For Class 9 Maths Chapter 1 Exercise 1.5 – Number System




NCERT Solutions For Class 9 Maths Chapter 1 Exercise 1.5 – Number System
1. Classify the following numbers as rational or irrational:
(i) 2 – √5
(ii) ( 3 + √23 ) – √23
(iii) (2√7/7√7)
(iv) 1/√2
(v) 2π
Solution:
(i) 2 – √5 : It is irrational.
(ii) ( 3 + √23 ) – √23 = 3 + √23 – √23 = 3 : It is rational.
(iii) (2√7/7√7) = 2/7 : It is rational
(iv) 1/√2 = : It is irrational.
(v) 2π : It is irrational.
Simplification of Irrational Numbers – Video Explanation
(2). Simplify each of the following expressions:
(i)( 3 + √3 )( 2 + √2 )
(ii)( 3 + √3 )( 3 – √3 )
(iii)(√5+√2)²
(iv)( √5 – √2 )( √5 + √2 )
Solution:
(i) ( 3 + √3 )( 2 + √2 )
( 3 + √3 )( 2 + √2 )
= ( 3 + √3 )2 +( 3 + √3 )√2
= 6 + 2√3 + 3√2 + √6
(ii)( 3 + √3 )( 3 – √3 )
Using the identity
( a + b )( a – b) = a2 – b2
We get
( 3 + √3 )( 3 – √3 ) = 3² – √32 = 9 – 3 = 6
(iii) (√5+√2)²
Using the identity
(a + b)² = a2 + 2ab + b2
We get
(√5+√2)² = 5 + 2 √10 + 2 = 7 + 2 √10
(iv)( √5 – √2 )( √5 + √2 )
Using the identity
( a – b )( a + b) = a2 – b2
We get
( √5 – √2 )( √5 + √2 ) = 5 – 2 = 3
(3) Recall, π is defined as the ratio of the circumference (say c) of a circle to its diameter (say d). That is, π = c/d. This seems to contradict the fact that π is irrational. How will you resolve this contradiction?
Solution:
As we measure c and d using any physical device we do not get the exact value manually , instead we get an approximate rational value and this is why this contradiction arises.
4. Represent √9.3 on the number line.
Solution:
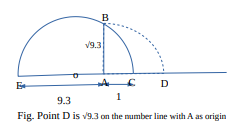
Follow the steps below to locate √9.3 on the number line as shown above:
Step (I) Draw a line segment of length 9.3 units EA and extend it to C by 1 unit .
Step (II) Now with O as mid point of EC draw a semicircle with O as center and OC as radius.
Step (III) Draw a line perpendicular to EC at A and intersecting the semicircle at B.
Step (IV) Taking A as center and AB as radius draw an arc from B to intersect the extended line EAC at D.
If we assign A as origin i.e. 0
Then D represents √9.3 on the number line as shown in the figure.

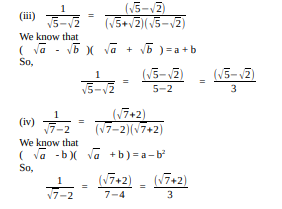
NCERT Solutions for Class 9 Maths Chapter 1 Exercise 1.5 – Number System, has been designed by the NCERT to test the knowledge of the student on the topic – Operations on Real Numbers
The next Exercise for NCERT Solutions for Class 9 Maths Chapter 1 Exercise 1.6 – Number System can be accessed by clicking here.
Download NCERT Solutions For Class 9 Maths Chapter 1 Exercise 1.5 – Number System
