NCERT Solutions for Class 8 Maths Chapter 9 Exercise 9.5 Algebraic Expressions & Identities
ncert solutions for class 8 maths chapter 9 exercise 9.5 contains 8 questions and each question has explained in detail and stepwise. If you are class 8th student and currently preparing chapter 9 exercise 9.1 then you must be looking for the class 8 maths chapter 9 exercise 9.5 solution for your exams preparation. Here we are providing complete solutions for class 8 maths chapter 9 exercise 9.5.
Table of Content
| Category | NCERT Solutions Class 8 |
| Subject | Maths |
| Chapter | Chapter 9 |
| Exercise | Exercise 9.5 |
| Chapter Name | Algebraic Expressions & Identities |
NCERT Solutions for Class 8 Maths Chapter 9 Exercise 9.5 – Algebraic Expressions & Identities, has been designed by the NCERT to test the knowledge of the student on the following topics:-
- What is an Identity?
- Standard Identities
- Applying Identities
NCERT Solutions For Class 8 Maths Chapter 9 Exercise 9.5
1. Use a suitable identity to get each of the following products.
i. (x + 3) (x + 3)
Sol.: – (x + 3) (x + 3)
= (x + 3)2
= x2 + 2 × x × 3 + 32 … { (a + b)2 = a2 + 2ab + b2 }
= x2 + 6x + 9
ii. (2y + 5) (2y + 5)
Sol.: – (2y + 5) (2y + 5)
= (2y + 5)2
= (2y)2 + 2 × (2y) × 5 + 52 … { (a + b)2 = a2 + 2ab + b2 }
= 4y2 + 20y + 25
iii. (2a – 7) (2a – 7)
Sol.: – (2a – 7) (2a – 7)
= (2a – 7)2
= (2a)2 – 2 × 2a × 7 + 72 … { (a – b)2 = a2 – 2ab + b2 }
= 4a2 – 28a + 49
iv. [3a – (1/2)] [3a – (1/2)]
Sol.: – [3a – (1/2)] [3a – (1/2)]
= [3a – (1/2)]2
= (3a)2 – 2 × 3a × (1/2) + (1/2)² .. { (a – b)2 = a2 – 2ab + b2 }
= 9a2 – 3a + (1/4)
v. (1.1m – 0.4) (1.1m + 0.4)
Sol.: – (1.1m – 0.4) (1.1m + 0.4)
= (1.1m)2 – (0.4)2 … { (a + b) (a – b) = a2 – b2 }
= 1.21m2 = 0.16
vi. (a2 + b2) (-a2 + b2)
Sol.: – (a2 + b2) (-a2 + b2)
= (b2 + a2) (b2 – a2)
= (b2)2 – (a2)2 … { (a + b) (a – b) = a2 – b2 }
= b4 – a4
vii. (6x – 7) (6x + 7)
Sol.: – (6x – 7) (6x + 7)
= (6x)2 – 72 … { (a + b) (a – b) = a2 – b2 }
= 36x2 – 49
viii. (-a + c) (-a +c)
Sol.: – (-a + c) (-a +c)
= (-a +c)2
= (c – a)2
= c2 – 2 × c × a + a2 .. { (a – b)2 = a2 – 2ab + b2 }
= c2 – 2ca + a2
= a2 – 2ac + c2
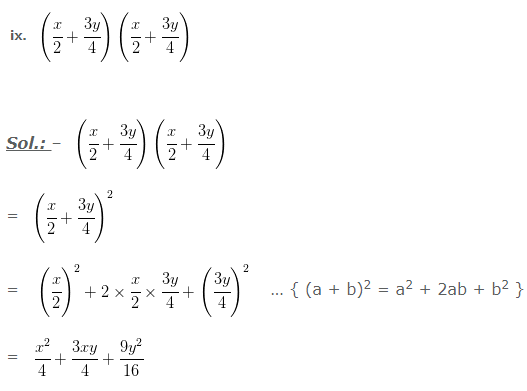
x. (7a – 9b) (7a – 9b)
Sol.: – (7a – 9b) (7a – 9b)
= (7a – 9b)2
= (7a)2 – 2 × 7a × 9b + (9b)2 .. { (a – b)2 = a2 – 2ab + b2 }
= 49a2 – 126ab + 81b2
2. Use the identity (x + a) (x + b) = x2 + (a + b) x + ab to find the following products.
i. (x + 3) (x + 7)
Sol.: – (x + 3) (x + 7)
= x2 + (3 + 7)x + 3 × 7
= x2 + 10x + 21
ii. (4x + 5) (4x +1)
Sol.: – (4x + 5) (4x +1)
= (4x)2 + (5 + 1)(4x) + 5 × 1
= 16x2 + 24x + 5
iii. (4x – 5) (4x – 1)
Sol.: – (4x – 5) (4x – 1)
= (4x)2 + ((-5) + (-1))(4x) + (-5) × (-1)
= 16x2 + (-5 – 1)(4x) + 5
= 16x2 – 24x + 5
iv. (4x + 5) (4x – 1)
Sol.: – (4x + 5) (4x – 1)
= (4x)2 + (5 + (-1))(4x) + 5 × (-1)
= 16x2 + (5 – 1)(4x) – 5
= 16x2 + 16x – 5
v. (2x + 5y) (2x + 3y)
Sol.: – (2x + 5y) (2x + 3y)
= (2x)2 + (5y + 3y)(2x) + 5y × 3y
= 4x2 + 8y × 2x + 15y2
= 4x2 + 16xy + 15y2
vi. (2a2 + 9) (2a2 + 5)
Sol.: – (2a2 + 9) (2a2 + 5)
= (2a2)2 + (9 + 5)(2a2) + 9 × 5
= 4a4 + 28a2 + 45
vii. (xyz – 4) (xyz – 2)
Sol.: – (xyz – 4) (xyz – 2)
= (xyz)2 + ((-4) + (-2))(xyz) + (-4) × (-2)
= x2y2z2 + (-4 – 2)(xyz) + 8
= x2y2z2 – 6xyz + 8
3. Find the following squares by using the identities.
i. (b – 7)2
Sol.: – (b – 7)2
= b2 – 2 × b × 7 + 72 … { (a – b)2 = a2 – 2ab + b2 }
= b2 – 14b + 49
2. (xy + 3z)2
Sol.: – (xy + 3z)2
= (xy)2 + 2 × xy × 3z + (3z)2 .. { (a + b)2 = a2 + 2ab + b2 }
= x2y2 + 6xyz + 9z2
3. (6x2 – 5y)2
Sol.: – (6x2 – 5y)2
= (6x2)2 – 2 × 6x2 × 5y + (5y)2 .. { (a – b)2 = a2 – 2ab + b2 }
= 36x4 – 60x2y + 25y2
4. [(2/3)m + (3/2)n]²
Sol.: – [(2/3)m + (3/2)n]²
= (2/3 m)² + 2 × (2/3)m ×(3/2)n + (3/2 n)² … { (a + b)2 = a2 + 2ab + b2 }
= (4/9)m²+2mn+(9/4)n²
v. (0.4p – 0.5q)2
Sol.: – (0.4p – 0.5q)2
= (0.4p)2 – 2 × 0.4p × 0.5q + (0.5q)2 .. { (a – b)2 = a2 – 2ab + b2 }
= 0.16p2 – 0.4pq + 0.25q2
vi. (2xy + 5y)2
Sol.: – (2xy + 5y)2
= (2xy)2 + 2 × 2xy × 5y + (5y)2 .. { (a + b)2 = a2 + 2ab + b2 }
= 4x2y2 + 20xy2 + 25y2
4. Simplify
i. (a2 – b2)2
Sol.: – (a2 – b2)2
= (a2)2 – 2 × a2 × b2 + (b)2 .. { (a – b)2 = a2 – 2ab + b2 }
= a4 – 2a2b2 + b4
ii. (2x + 5)2 – (2x – 5)2
Sol.: – (2x + 5)2 – (2x – 5)2
= {(2x + 5) + (2x – 5)} {(2x + 5) – (2x – 5)} .. { (a2 – b2) = (a + b) (a – b)
= (2x + 5 + 2x – 5) (2x + 5 – 2x + 5)
= (4x)(10)
= 40x
Or
(2x + 5)2 – (2x – 5)2 .. { (a + b)2 = a2 + 2ab + b2 } and { (a – b)2 = a2 – 2ab + b2 }
= {(2x)2 + 2 × 2x × 5 + 52} – {(2x)2 – 2 × 2x × 5 + 52}
= (4x2 + 20x +25) – (4x2 – 20x + 25)
= 4x2 + 20x + 25 – 4x2 + 20x – 25
= 40x
iii. (7m – 8n)2 + (7m + 8n)2
Sol.: – (7m – 8n)2 + (7m + 8n)2
= {(7m)2 – 2 × 7m × 8n + (8n)2} + {(7m)2 + 2 × 7m × 8n + (8n)2} … { (a + b)2 = a2 + 2ab + b2 } and { (a – b)2 = a2 – 2ab + b2 }
= 49m2 – 112mn + 64n2 + 49m2 + 112mn + 64n2
= 98m2 + 128n2
iv. (4m + 5n)2 + (5m + 4n)2
Sol.: – (4m + 5n)2 + (5m + 4n)2
= {(4m)2 + 2 × 4m × 5n + (5n)2} + {(5m)2 + 2 × 5m × 4n + (4n)2} .. { (a + b)2 = a2 + 2ab + b2 }
= 16m2 + 40mn + 25n2 + 25m2 + 40mn + 16n2
= 41m2 + 80mn + 41n2
v. (2.5p – 1.5q)2 – (1.5p – 2.5q)2
Sol.: – (2.5p – 1.5q)2 – (1.5p – 2.5q)2
= {(2.5p – 1.5q) + (1.5p – 2.5q)} {(2.5p – 1.5q) – (1.5p – 2.5q)} .. { (a2 – b2) = (a + b) (a – b)
= {2.5p – 1.5q + 1.5p – 2.5q} {2.5p – 1.5q – 1.5p + 2.5q}
= (4p – 4q) (p + q) (taking 4 common)
= 4(p – q) (p + q)
= 4(p2 – q2) .. { (a + b) (a – b) = a2 – b2 }
= 4p2 – 4q2
vi. (ab + bc)2 – 2ab2c
Sol.: – (ab + bc)2 – 2ab2c
= (ab)2 + 2 × ab × bc + (bc)2 – 2ab2c .. { (a + b)2 = a2 + 2ab + b2 }
= a2b2 + 2ab2c + b2c2 – 2ab2c
= a2b2 + b2c2
vii. (m2 – n2m)2 + 2m3n2
Sol.: – (m2 – n2m)2 + 2m3n2
= (m2)2 – 2 × m2 × n2m + (n2m)2 + 2m3n2 .. { (a – b)2 = a2 – 2ab + b2 }
= m4 – 2m3n2 + n4m2 + 2m3n2
= m4 + n4m2
5. Show that.
i. (3x + 7)2 – 84x = (3x – 7)2
Sol.: – L.H.S. = (3x + 7)2 – 84x
= (3x)2 + 2 × 3x × 7 + 72 – 84x .. { (a + b)2 = a2 + 2ab + b2 }
= (3x)2 + 42x + 72 – 84x
= (3x)2 – 42x + 72
= (3x)2 – 2 × 3x × 7 + 72
= (3x – 7)2 .. { (a – b)2 = a2 – 2ab + b2 }
= R.H.S.
ii. (9p – 5q)2 + 180pq = (9p + 5q)2
Sol.: – L.H.S. = (9p – 5q)2 + 180pq
= (9p)2 – 2 × 9p × 5q + (5q)2 + 180pq .. { (a – b)2 = a2 – 2ab + b2 }
= (9p)2 – 90pq + (5q)2 + 180pq
= (9p)2 + 90pq + (5q)2
= (9p)2 + 2 × 9p × 5q + (5q)2
= (9p + 5q)2 .. { (a + b)2 = a2 + 2ab + b2 }
= R.H.S.
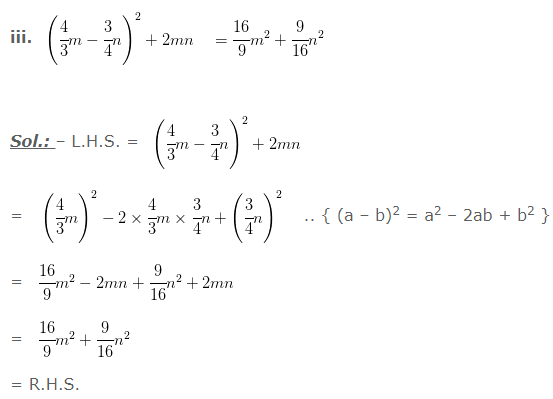
iv. (4pq + 3q)2 – (4pq – 3q)2 = 48pq2
Sol.: – L.H.S. = (4pq + 3q)2 – (4pq – 3q)2
= {(4pq + 3q) + (4pq – 3q)} {(4pq + 3q) – (4pq – 3q)} .. { (a2 – b2) = (a + b) (a – b)}
= {4pq + 3q + 4pq – 3q} {4pq + 3q – 4pq + 3q)}
= (8pq) (6q)
= 48pq2
= R.H.S.
v. (a – b) (a + b) + (b – c) (b + c) + (c – a) (c + a) = 0
Sol.: – L.H.S. = (a – b) (a + b) + (b – c) (b + c) + (c – a) (c + a)
= a2 – b2 + b2 – c2 + c2 – a2 .. { (a + b) (a – b) = a2 – b2 }
= 0
= R.H.S.
6. Using identities, evaluate.
i. 712
Sol.: – 712
= (70 + 1)2
= 702 + 2 × 70 × 1 + 12 .. { (a + b)2 = a2 + 2ab + b2 }
= 4900 + 140 + 1
= 5041
ii. 992
Sol.: – 992
= (100 – 1)2
= 1002 – 2 × 100 × 1 + 12 .. { (a – b)2 = a2 – 2ab + b2 }
= 10000 – 200 + 1
= 9801
iii. 1022
Sol.: – 1022
= (100 + 2)2
= 1002 + 2 × 100 × 2 + 22 .. { (a + b)2 = a2 + 2ab + b2 }
= 10000 + 400 + 4
= 10404
iv. 9982
Sol.: – 9982
= (1000 – 2)2
= 10002 – 2 × 1000 × 2 + 22 .. { (a – b)2 = a2 – 2ab + b2 }
= 1000000 – 4000 + 4
= 996004
v. 5.22
Sol.: – 5.22
= (5 + 0.2)2
= 52 + 2 × 5 × 0.2 + 0.22 .. { (a + b)2 = a2 + 2ab + b2 }
= 25 + 2 + 0.04
= 27.04
vi. 297 × 303
Sol.: – 297 × 303
= (300 – 3) (300 + 3)
= 3002 – 32 .. { (a + b) (a – b) = a2 – b2 }
= 90000 – 9
= 89991
vii. 78 × 82
Sol.: – 78 × 82
= (80 – 2) (80 + 2)
= 802 – 22 .. { (a + b) (a – b) = a2 – b2 }
= 6400 – 4
= 6396
viii. 8.92
Sol.: – 8.92
= (9 – 0.1)2
= 92 – 2 × 9 × 0.1 + 0.12 .. { (a – b)2 = a2 – 2ab + b2 }
= 81 – 1.8 + 0.01
= 79.21
ix. 1.05 × 9.5
Sol.: – 1.05 × 9.5
= (1 + 0.05) (1 + 8.5)
= 12 + (0.05 + 8.5) × 1 + 0.05 × 8.5 …… { (x + a) (x + b) = x2 + (a + b) x + ab }
= 1 + 8.55 + 0.425
= 9.975
7. Using a2 – b2 = (a + b) (a – b), find
i. 512 – 492
Sol.: – 512 – 492
= (51 + 49) (51 – 49)
= 100 × 2
= 200
ii. (1.02)2 – (0.98)2
Sol.: – (1.02)2 – (0.98)2
= (1.02 + 0.98) (1.02 – 0.98)
= 2 × 0.04
= 0.08
iii. 1532 – 1472
Sol.: – 1532 – 1472
= (153 + 147) (153 – 147)
= 300 × 6
= 1800
iv. 12.12 – 7.92
Sol.: – 12.12 – 7.92
= (12.1 + 7.9) (12.1 – 7.9)
= 20 × 4.2
= 84
8. Using (x + a) (x + b) = x2 + (a + b) x + ab, find
i. 103 × 104
Sol.: – 103 × 104
= (100 + 3) (100 + 4)
= 1002 + (3 + 4) × 100 + 3 × 4
= 10000 + 700 + 12
= 10712
ii. 5.1 × 5.2
Sol.: – 5.1 × 5.2
= (5 + 0.1) (5 + 0.2)
= 52 + (0.1 + 0.2) × 5 + 0.1 × 0.2
= 25 + 1.5 + 0.02
= 26.52
iii. 103 × 98
Sol.: – 103 × 98
= (100 + 3) (100 – 2)
= 1002 + (3 + (-2)) × 100 + 3 × (-2)
= 10000 + (3 – 2) × 100 – 6
= 10000 + 100 – 6
= 10094
iv. 9.7 × 9.8
Sol.: – 9.7 × 9.8
= (10 – 0.3) (10 – 0.2)
= 102 + ((-0.3) + (-0.2)) × 10 + (-0.3) × (-0.2)
= 100 + (-0.3 – 0.2) × 10 + 0.06
= 100 – 5 + 0.06
= 95.06
Other Exercise’s NCERT solutions for class 8 maths chapter 9
- Exercise 9.1 – Algebraic Expressions and Identities
- Exercise 9.2 – Algebraic Expressions and Identities
- Exercise 9.3 – Algebraic Expressions and Identities
- Exercise 9.4 – Algebraic Expressions and Identities
- Exercise 9.5 – Algebraic Expressions and Identities
NCERT Solutions For Class 8 Maths Chapter 9 Exercise 9.5 – Algebraic Expressions & Identities
