NCERT Solutions for Class 8 Maths Chapter 9 Exercise 9.3 Algebraic Expressions & Identities
NCERT Solutions for Class 8 Maths Chapter 9 Exercise 9.3 contains 4 questions and each question has explained in detail and stepwise. If you are class 8th student and currently preparing chapter 9 exercise 9.3 then you must be looking for the maths class 8 chapter 9 exercise 9.3 solution for your exams preparation. Here we are providing complete solutions for class 8 maths exercise 9.3.
Table of Content
| Category | NCERT Solutions Class 8 |
| Subject | Maths |
| Chapter | Chapter 9 |
| Exercise | Exercise 9.3 |
| Chapter Name | Algebraic Expressions & Identities |
NCERT Solutions for Class 8 Maths Chapter 9 Exercise 9.3 Algebraic Expressions & Identities, has been designed by the NCERT to test the knowledge of the student on the topic Multiplying a Monomial by a Polynomial
- Multiplying a monomial by a binomial
- Multiplying a monomial by a trinomial
NCERT Solutions For Class 8 Maths Chapter 9 Exercise 9.3 Algebraic Expressions & Identities
Q.1 Carry out the multiplication of the expressions in each of the following pairs.
(i) 4p, q + r
(ii) ab, a – b
(iii) a + b, 7a2b2
(iv) a2 − 9, 4a
(v) pq + qr + rp, 0
Solution:
(i) (4p)×(q+r)=(4p×q)+(4p×r)=4pq+4pr
(ii) (ab)×(a-b)=(ab×a)+[ab×(- b)]=a²b-ab²
(iii) (a+b)×(7a²b²)=(a×7a²b²)+(b×7a²b²)=7a³b²+7a²b³
(iv) (a²-9)×(4a)=(a²×4a)+(- 9)×(4a)=4a³-36a
(v) (pq+qr+rp)×0=(pq × 0)+(qr×0)+(rp×0)=0
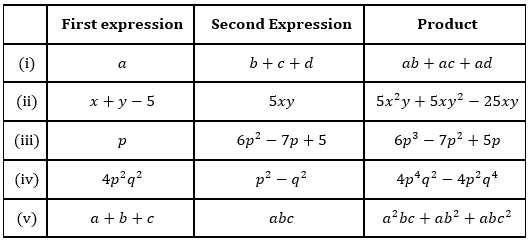
Q.2 Complete the table

Solution:
Q.3 Find the product.
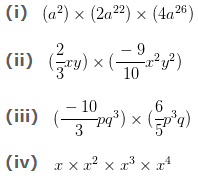
Solution:
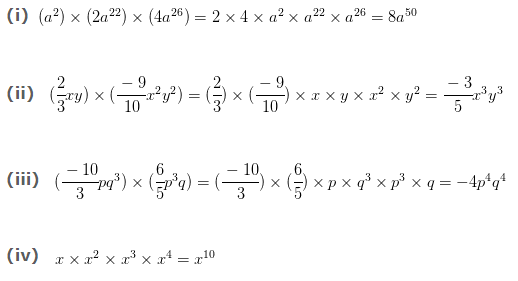
Q.4
(a) Simplify 3x (4x −5) + 3 and find its values for (i) x = 3, (ii) x = 1/2
(b) Simplify a (a2 + a + 1) + 5 and find its values for (i) a = 0, (ii) a = 1, (iii) a = − 1
Solution:
(a) 3x (4x − 5) + 3 = 12x2 − 15x + 3
(i) For x = 3,
12x2 − 15x + 3 = 12 (3)2 − 15(3) + 3
= 108 − 45 + 3
= 66
(ii) For x = ½
12x2 − 15x + 3 = 12 (1/2)2 − 15(1/2) + 3
= 3 – 15/2 + 3
= 6 – 15/2
= – 3/2
(b) a (a2 + a + 1) + 5 = a3 + a2 + a + 5
(i) For a = 0,
a3 + a2 + a + 5 = 0 + 0 + 0 + 5
= 5
(ii) For a = 1,
a3 + a2 + a + 5 = (1)3 + (1)2 + 1 + 5
= 1 + 1 + 1 + 5 = 8
(iii) For a = −1,
a3 + a2 + a + 5 = (−1)3 + (−1)2 + (−1) + 5
= − 1 + 1 − 1 + 5 = 4
Q.5
(a) Add: p(p-q),q(q-r) and r(r-p)
(b) Add: 2x(z-x-y) and 2y(z-y-x)
(c) Subtract: 3l(l-4m+5n) from 4l(10n-3m+2l)
(d) Subtract: 3a(a+b+c)-2b(a-b+c) from 4c(- a+b+c)
Solution:
(a) First expression = p (p − q) = p2 – pq
Second expression = q (q − r) = q2 – qr
Third expression = r (r − p) = r2 − pr
Adding three expressions, we get
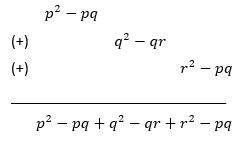
Therefore, sum of the three given expressions is p2 + q2 + r2 − pq − qr – rp
(b) First expression = 2x (z − x − y) = 2xz − 2x2 − 2xy
Second expression = 2y (z − y − x) = 2yz − 2y2 − 2yx
Adding two expressions, we get
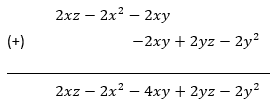
Therefore, sum of the two given expressions is − 2x2 − 2y2 − 4xy + 2yz + 2zx.
(c) First expression = 3l (l − 4m + 5n) = 3l2 − 12lm + 15ln
Second expression = 4l (10n − 3m + 2l) = 40ln − 12lm + 8l2
Subtracting first expression from second, we get

Therefore, Subtracting 3l(l-4m+5n) from 4l(10n-3m+2l)
we get 25ln+5l²
(d) First expression = 3a (a + b + c) − 2b (a − b + c) = 3a2 +3ab + 3ac − 2ba + 2b2 − 2bc
= 3a2 + 2b2 + ab + 3ac − 2bc
Second expression = 4c (− a + b + c) = − 4ac + 4bc + 4c2
Subtracting first expression from second, we get
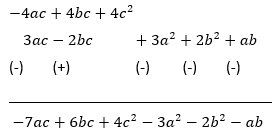
Therefore, Subtract: 3a(a+b+c)-2b(a-b+c) from 4c(- a+b+c)
we get, -7ac+6bc+4c²-3a²-2b²-ab
Other Exercise’s NCERT solutions for class 8 maths chapter 9
- Exercise 9.1 – Algebraic Expressions and Identities
- Exercise 9.2 – Algebraic Expressions and Identities
- Exercise 9.3 – Algebraic Expressions and Identities
- Exercise 9.4 – Algebraic Expressions and Identities
- Exercise 9.5 – Algebraic Expressions and Identities
The next Exercise for NCERT Solutions for Class 8 Maths Chapter 9 Exercise 9.4 Algebraic Expressions and Identities can be accessed by clicking here
NCERT Solutions For Class 8 Maths Chapter 9 Exercise 9.3 Algebraic Expressions and Identities
