NCERT Solutions for Class 8 Maths Chapter 8 Exercise 8.3 Comparing Quantities

NCERT Solutions for Class 8 Maths Chapter 8 Exercise 8.3

NCERT solutions for class 8 maths chapter 8 exercise 8.3 contains 6 questions and each question has explained in detail and stepwise. If you are class 8th student and currently preparing ex 8.3 class 8 maths then you must be looking for the class 8 maths chapter 8 exercise 8.3 solution for your exams preparation. Here we are providing complete solutions for class 8 exercise 8.3.

Table of Content

Category NCERT Solutions Class 8
Subject Maths
Chapter Chapter 8
Exercise Exercise 8.3
Chapter Name Comparing Quantities

NCERT Solutions for Class 8 Maths Chapter 8 Exercise 8.3 Comparing Quantities, has been designed by the NCERT to test the knowledge of the student on the following topics:

  • Compound Interest
  • Deducing a Formula for Compound Interest
  • Rate Compounded Annually or Half Yearly (Semi Annually)
  • Applications of Compound Interest Formula




NCERT Solutions for Class 8 Exercise 8.3 Chapter 8 Maths Comparing Quantities

Q.1 Calculate the amount and compound interest on

(a) Rs. 10,800 for 3 years at 12\cfrac { 1 }{ 2 } % per annum compounded annually.
(b) Rs. 18,000 for 2\cfrac { 1 }{ 2 } years at 10% per annum compounded annually.
(c) Rs. 62,500 for 1\cfrac { 1 }{ 2 } years at 8% per annum compounded half yearly.
(d) Rs. 8,000 for 1 year at 9% per annum compounded half yearly.
(e) Rs. 10,000 for 1 year at 8% per annum compounded half yearly.

Solution:

(a) Principal (P) = Rs. 10,800
Rate of interest (R) = 12\cfrac { 1 }{ 2 } % = \cfrac { 25 }{ 2 } %
Number of years (n) = 3 [ Time Period ]
Amount (A) = P{ \left( 1+\cfrac { R }{ 100 } \right) }^{ n }
A = 10800{ \left( 1+\cfrac { 25 }{ 200 } \right) }^{ 3 }
A = 10800{ \left( \cfrac { 225 }{ 200 } \right) }^{ 3 }
A = Rs. 15377.3
Compound interest ( C.I ) = A – P = 15377.3 – 10800 = Rs. 4,577.3

(b) Principal (P) = Rs. 18,000
Rate of interest (R) = 10%
Number of years (n) = 2\cfrac { 1 }{ 2 } [ Time Period ]
As the Time period is two and half years, Amount is calculated by first calculating the amount for 2 years using the compound interest formula, and then calculating the simple interest for 6 months on the amount obtained at the end of 2 years
Amount for two years:
(A) =P{ \left( 1+\cfrac { R }{ 100 } \right) }^{ n }
A = 18000{ \left( 1+\cfrac { 10 }{ 100 } \right) }^{ 2 }
A = 21780
Interest for first two years is A – P = 21780 – 18000 = 3780
Now taking Rs. 21780 as the principal, Simple Interest for next 6 months has to be calculated:
S.I. = \cfrac { P\times T\times R }{ 100 }
= \cfrac { 21780\times \cfrac { 1 }{ 2 } \times 10 }{ 100 }
= 1089
Interest for next 6 months = Rs. 1089
Therefore, total compound Interest = 3780 + 1089 = 4869
A = 18,000 + 4869 = Rs. 22,869

(c) Principal (P) = Rs. 62,500
Rate of interest (R) = 8% = 4% per half year
Number of years (n) = 1\cfrac { 1 }{ 2 } [ Time Period ]
As the interest is calculated half yearly, there are three half years in 1\cfrac { 1 }{ 2 } years

A = 62500{ \left( 1+\cfrac { 4 }{ 100 } \right) }^{ 3 }
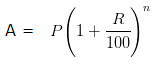
A = Rs. 70304
Compound Interest (C.I.) = 70304 – 62500=Rs. 7,804




(d) Principal (P) = Rs. 8000
Rate of interest (R) = 9% = \cfrac { 9 }{ 2 } % per half year
Number of years (n) = 1 [ Time Period ]
As the interest is calculated half yearly, there are two half years in  year

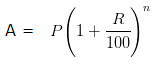
A = 8000{ \left( 1+\cfrac { 9 }{ 200 } \right) }^{ 2 }
A = Rs. 8736.20
Compound Interest (C.I.) = 8736.20 – 8000 = Rs. 736.20

(e) Principal (P) = Rs. 10000
Rate of interest (R) = 8% = 4% per half year
Number of years (n) = 1 [ Time Period ]
As the interest is calculated half yearly, there are two half years in  year

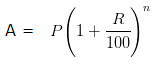
A = 10000{ \left( 1+\cfrac { 4 }{ 100 } \right) }^{ 2 }
A = Rs. 10,816
Compound Interest (C.I.) = 10816 – 10000 = Rs. 816

Q.2 Kamala borrowed Rs 26400 from a Bank to buy a scooter at a rate of 15% p.a. compounded yearly. What amount will she pay at the end of 2 years and 4 months to clear the loan?

(Hint: Find A for 2 years with interest is compounded yearly and then find SI on the 2nd year amount for 4/12 years)

Solution:

Given, Kamala borrowed Rs 26400 from a Bank to buy a scooter at a rate of 15% per annum compounded yearly
Principal (P) = Rs 26,400
Rate of interest (R) = 15% per annum
Number of years (n) = 2\cfrac { 4 }{ 12 } years
As the time period is Two years and Four months, the amount is calculated by first calculating the amount for 2 years using the compound interest and then calculating the simple interest for 4 months on the amount obtained for the first two years
Amount for two years:

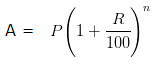
A = 26400{ \left( 1+\cfrac { 15 }{ 100 } \right) }^{ 2 }
A = Rs. 34914
Interest for the first two years = 34914 − 26400 = Rs. 8514
Now taking Rs. 34914 as the principal, simple interest for next 4 months has to be calculated:
S.I. = \cfrac { P\times T\times R }{ 100 }
S.I, = \cfrac { 34914\times \cfrac { 4 }{ 12 } \times 15 }{ 100 }
S.I. = 1745.70
Interest for next 4 months = Rs. 1745.70
Therefore, Total C.I. = 8514 + 1745.70 = Rs. 10,259.70
Amount = P + C.I. = 26400 + 10259.70 = Rs. 36,659.70
Therefore, Kamala would pay Rs. 36,659.70 at the end of years and 4 months to clear the loan

 

Q.3. Fabina borrows Rs 12,500 at 12% per annum for 3 years at simple interest and Radha borrows the same amount for the same time period at 10% per annum, compounded annually. Who pays more interest and by how much?

Solution:

Given, Fabina borrows Rs 12,500 at 12% per annum for 3 years at simple interest and Radha borrows the same amount for the same time period at 10% per annum, compounded annually
Interest paid by Fabina (S.I.) = \cfrac { P\times T\times R }{ 100 }
12500 x 3 x \cfrac { 12 }{ 100 } = Rs. 4500

Interest paid by Radha (C.I) = P{ \left( 1+\cfrac { R }{ 100 } \right) }^{ n } – P
= 12500{ \left( 1+\cfrac { 10 }{ 100 } \right) }^{ 3 } – 12500
= 16637.50 – 12500 = Rs. 4137.50
Interest paid bt Fabina is Rs. 4500 whereas interest paid by Radha is Rs. 4137.50
Therefore, Fabina pays more interest
4500 – 4137.50 = Rs. 362.50




Q.4 I borrowed Rs 12000 from Jamshed at 6% per annum simple interest for 2 years. Had I borrowed this sum at 6% per annum compound interest, what extra amount would I have to pay?

Solution:

Given, I borrowed Rs. 12000 from Jamshed at 6% p.a. simple interest for 2 years
Principal (P) = Rs. 12000
Rate of interest (R) = 6% per annum
Time = 2 years
Simple Interest (S.I.) = \cfrac { P\times T\times R }{ 100 }
= 12000 x 2 x \cfrac { 6 }{ 100 } = Rs. 1440
Compound Interest (C.I.) = P{ \left( 1+\cfrac { R }{ 100 } \right) }^{ n } – P
12000{ \left( 1+\cfrac { 6 }{ 100 } \right) }^{ 2 } – 12000
= 13483.20 – 12000
= Rs. 1483.20
C.I. = Rs. 1,483.20
S.I. = Rs. 1,440.00
C.I. – S.I. = Rs. 1,483.20 – Rs. 1,440.00 = Rs. 43.20
Therefore, the extra amount to be paid is Rs. 43.20

Q.5 Vasudevan invested Rs 60000 at an interest rate of 12% per annum compounded half yearly. What amount would he get
(i) after 6 months?
(ii) after 1 year?

Solution:

Given, Vasudevan invested Rs 60000 at an interest rate of 12% per annum compounded half yearly
(i) Principal (P) = Rs. 60000
Rate of interest = 12% per annum = 6% per half year
Time (n) = 6 months (1 half year )

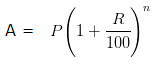
A = 60000{ \left( 1+\cfrac { 6 }{ 100 } \right) }^{ 1 }
A = 63600
Therefore, the amount Vasudevan would get after 6 months is Rs. 63600

(ii) Principal (P) = Rs. 60000
Rate of interest = 12% per annum = 6% per half year
Time (n) = 12 months (2 half years )

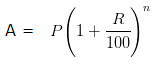
A = 60000{ \left( 1+\cfrac { 6 }{ 100 } \right) }^{ 2 }
A = 67416
Therefore, the amount Vasudevan would get after 12 months is Rs. 67416

Q.6 Arif took a loan of Rs 80,000 from a bank. If the rate of interest is 10% per annum, find the difference in amounts he would be paying after 1\cfrac { 1 }{ 2 }  years if the interest is 

(i) Compounded annually
(ii) Compounded half yearly

 Solution:

Given, Arif took a loan of Rs 80,000 from a bank. If the rate of interest is 10% per annum

(i) Principal (P) = Rs 80000
Rate of interest = 10% per annum
Time (n) = 1\cfrac { 1 }{ 2 } years
As the time period is 1 year and 6 months, the amount can be calculated by first calculating the amount for 1 year using the compound interest, and then calculating the simple interest for 6 months on the amount obtained at the end of 1 year.
Amount for 1 year:

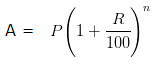
A = 80000{ \left( 1+\cfrac { 10 }{ 100 } \right) }^{ 1 }
A = Rs. 88000
Interest for the first 1 year = 88000 – 80000 = Rs. 8000
Now taking Pricipal (P) as Rs. 88000, Simple interest for next 6 months has to be calculated:
S.I. = \cfrac { P\times T\times R }{ 100 }
S.I. = \cfrac { 88000\times \cfrac { 1 }{ 2 } \times 10 }{ 100 }
S.I. = Rs. 4400
Interest for next 6 months = Rs. 4400
Total Compound Interest (C.I.) = 8000 + 4400 = Rs. 12400
Total Amount (A) = P + C.I. = 80000 + 12400 = Rs. 92400

(ii) interest is compounded half yearly
Principal (P) = Rs 80000
Rate of interest = 10% per annum = 5% per half year
Time (n) = 1\cfrac { 1 }{ 2 } years ( 3 half years )

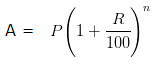
A = 80000{ \left( 1+\cfrac { 5 }{ 100 } \right) }^{ 3 }
A = Rs. 92610
Difference between the amounts that Arif would pay when the interest is compounded half yearly and annually = 92610 – 92400 = Rs. 210

Q.7 Maria invested Rs. 8000 in a business. She would be paid interest at 5% per annum compounded annually. Find.

(i) The amount credited against her name at the end of the second year
(ii) The interest for the 3rd year

Solution:

Given, Maria invested Rs. 8000 in a business. She would be paid interest at 5% per annum compounded annually

(i) P = Rs. 8000
R = 5% per annum
n = 2 years

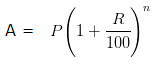
A=8000{ \left( 1+\cfrac { 5 }{ 100 } \right) }^{ 2 }
A = Rs. 8820
Amount that would be credited at the end of second year is Rs. 8820

(ii) interest for the third year can be calculated by taking Rs. 8820 as principal and calculating the S.I. for the next year
S.I.=\cfrac { P\times T\times R }{ 100 }
S.I. = \cfrac { 8820\times 1 \times 5 }{ 100 }
S.I. = Rs. 441
Interest for the third year is Rs. 441




Q.8 Find the amount and the compound interest on Rs 10,000 for 1\cfrac { 1 }{ 2 }  years at 10% per annum, compounded half yearly. Would this interest be more than the interest he would get if it was compounded annually?

Solution:

Given,
Principal (P) = Rs. 10000
Rate = 10% per annum = 5% per half year
n = 1\cfrac { 1 }{ 2 } years ( 3 half years )

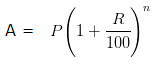
A=10000{ \left( 1+\cfrac { 5 }{ 100 } \right) }^{ 3 }
A = Rs. 11576.25
Compound Interest (C.I.) = A − P = 11576.25 − 10000 = Rs. 1576.25
As the time period is 1 year and 6 months, the amount can be calculated by first calculating the amount for 1 year using the compound interest, and then calculating the simple interest for 6 months on the amount obtained at the end of 1 year.
Amount for 1 year:

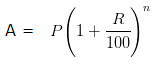
A=10000{ \left( 1+\cfrac { 10 }{ 100 } \right) }^{ 1 }
A = Rs. 11000
Interest for the first 1 year = 11000 – 10000 = Rs. 1000
Now taking Principal (P) as Rs. 11000, Simple interest for next 6 months has to be calculated:
S.I.=\cfrac { P\times T\times R }{ 100 }
S.I. = \cfrac { 11000\times \cfrac { 1 }{ 2 } \times 10 }{ 100 }
S.I. = Rs. 550
Interest for next 6 months = Rs. 550
Total Compound Interest (C.I.) = 1000 + 550 = Rs. 1550
1576 > 1550
Therefore, the interest would be more when compounded half yearly than the interest when compounded annually

Q.9 Find the amount which Ram will get on Rs. 4096,he gave it for 18 months at 12\cfrac { 1 }{ 2 } % per annum, interest being compounded half yearly.

Solution:

Given,
P = Rs 4,096
R = 12\cfrac { 1 }{ 2 } % per annum = \cfrac { 25 }{ 4 }% per half year
n = 18 months ( 3 half years )
A=P{ \left( 1+\cfrac { R }{ 100 } \right) }^{ n }
A=4096{ \left( 1+\cfrac { 25 }{ 400 } \right) }^{ 3 }
A = Rs. 4913
Therefore, Ram will get an amount of Rs. 4913

Q.10 The population of a place increased to 54000 in 2003 at a rate of 5% per annum 

(i) find the population in 2001
(ii) what would be its population in 2005?

Solution:

(i) Given, population of a place increased to 54000 in 2003 at a rate of 5% per annum.
Let, population be x in 2001
54000=x{ \left( 1+\cfrac { 5 }{ 100 } \right) }^{ 2 }
x = 54000 x \cfrac { 20 }{ 12 } x \cfrac { 20 }{ 21 }
= 48979.6
Therefore, the population in 2001 is 48980

(ii) Population in 2005:
54000{ \left( 1+\cfrac { 5 }{ 100 } \right) }^{ 2 }
= 59535
Therefore, the population in 2005 would be 59535

Q.11 In a laboratory, the count of bacteria in a certain experiment was increasing at the rate of 2.5% per hour. Find the bacteria at the end of 2 hours if the count was initially 5,06,000.

Solution:

Given,
Rate of bacteria increasing at 2.5% per hour
The initial count of bacteria is 5,06,000.
Bacteria at the end of 2 hours be x
x = 506000{ \left( 1+\cfrac { 2.5 }{ 100 } \right) }^{ 2 }
= 531616.25
Therefore, count of bacteria at the end of 2 hours would be 5,31,616 (approx)




Q.12 A scooter was bought at Rs 42,000. Its value depreciated at the rate of 8% per annum. Find its value after one year.

Solution:

Given, A scooter was bought at Rs 42,000
Its value depreciated at the rate of 8% per annum
Cost price of the scooter = Principal (P) = Rs 42,000
Depreciation = Rate of decrease = 8% per year
Value of scooter after one year:
= \cfrac { 42000\times 1\times 8 }{ 100 }
= 3360
Therefore, value of scooter after 1 year = 42000 − 3360 = Rs. 38640

NCERT Solutions for Class 8 Maths Chapter 9

The next Exercise for NCERT Solutions for Class 8 Maths Chapter 9 Exercise 9.1 Algebraic Expressions and Identities can be accessed by clicking here

Download NCERT Solutions for Class 8 Maths Chapter 8 Exercise 8.3 Comparing Quantities

NCERT Solutions for Class 8

CBSE Notes for Class 8

Worksheets for Class 8

Leave a Comment