Download NCERT Solutions for Class 8 Maths Chapter 16 Exercise 16.1 – Playing with Numbers. This Exercise contains 10 questions, for which detailed answers have been provided in this note. In case you are looking at studying the remaining Exercise for Class 8 for Maths NCERT solutions for Chapter 16 or other Chapters, you can click the link at the end of this Note.
NCERT Solutions for Class 8 Maths Chapter 16 Exercise 16.1 – Playing with Numbers





NCERT Solutions for Class 8 Maths Chapter 16 Exercise 16.1 – Playing with Numbers
Find the values of the letters in each of the following and give reasons for the steps involved.
1)
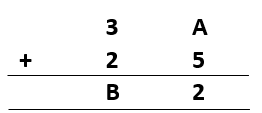
Sol.: – To find value of A, we need to put different values from 1 to 9 in place of A. Such that their addition with 5 will give 2 at unit place. On checking we found that 5 +7 = 12, having 2 at unit place. So, A = 7.
Now, to find value of B, we will add 35 and 25 which gives us 62.
So, B = 6.
Hence, A = 7 and B = 6
2)
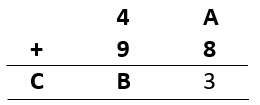
Sol.: – To find value of A, we need to put different values from 1 to 9 in place of A. Such that their addition with 8 will give 3 at unit place. On checking we found that 8 + 5 = 13, having 3 at unit place. So, A = 5.
Now, to find value of B and C, we will add 45 and 98 which gives us 143.
So, B = 4 and C = 1
Hence, A = 5, B = 4 and C = 1
3)

Sol.: – Here, it is given that A × A gives A at unit place.
So, we need to check for the number which satisfy this condition by putting different values of ‘A’ from 1 to 9. After checking we see that for value of A = 0, 1, 5, 6 the condition is satisfied.
Now, we need to check these values of ‘A’ to check they satisfy the condition “1 A × A = 9 A”.
For A = 0,
1 0 × 0 = 0
It doesn’t satisfy the above condition as tens place in not 9.
Similarly, for ‘A’ = 1,
1 1 × 1 = 11
It doesn’t satisfy the above condition as tens place in not 9.
And, for A = 5,
1 5 × 5 = 75
It doesn’t satisfy the above condition as tens place in not 9.
And, for A = 6,
1 6 × 6 = 96
For A = 6, all conditions are satisfied.
So, A = 6 will satisfy this Question.
4)

Sol.: – As B can be anything from 0 to 9, so B + 7 will be between 7 to 16. So, we can say that either
‘A + 3 = 6’ or ‘1 + A + 3 = 6’.

Putting values for A in ‘B + 7 = A’: –
As ‘B’ is getting added in 7, so resultant addition will be greater than 7,
i.e. ‘B + 7’ can be either 12 or 13 as ‘A’ is 2 or 3.
So, A = 2 and B = 5 will satisfy this Question.
5)

Sol.: – As B × 3 = B. So, possible values of B is 0, 5.
For B = 0,
Given, A × 3 = CA. To satisfy this condition only A = 5 can be placed.
Which makes A × 3 = 15 i.e. CA.
And for B = 5,
2nd term will become, 1 + A × 3 = CA. (As 1 will be carried forward from B × 3 = 15)
No value of ‘A’ satisfies this condition.
So, A = 5, B = 0 and C = 1 will satisfy this Question.
6)

Sol.: – As B × 5 = B (i.e. when 5 is multiplied by ‘B’ we get B at unit place).
For different values of B from 0 to 9, this condition can only be meet at B = 0 or 5.
For verification of value of B and finding A and C, let’s put both values of B in question.
For B = 0,

From this we get, A × 5 = CA (i.e. when 5 is multiplied by ‘A’ we get ‘A’ at unit place).
To satisfy this condition, A = 0 or 5 can be put in place of A. But as A and B are two different variables, we can’t assume both A and B as ‘0’ at the same time. So, for B = 0, only A = 5 can be accepted.
So, for A = 5
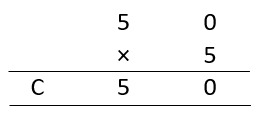
i.e. 50 × 5 = 250 = C 5 0.
This satisfies all condition.
Which makes A = 5, B = 0 and C = 2
And for B = 5,

We get, A × 5 + 2(carry forwarded from 5 × 5 = 25) = C A.
To satisfy this condition, A = 2 or 7 can be put in place of A.

So, values of A, B and C which satisfy this question are:-
- A = 5, B = 0 and C = 2
- A = 2, B = 5 and C = 1
- A = 7, B = 5 and C = 3
7)

Sol.: – As B × 6 = B, to satisfy this condition B = 0, 2, 4, 6, 8 can be placed.
For verification of value of B and finding A, let’s put different values of B in question.
For B = 0,
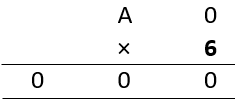
This is not possible as A × 6 ≠ 0. Since A ≠ B.
For B = 2,

To satisfy this condition, A × 6 must become 21. Which is not possible.
For B = 4,
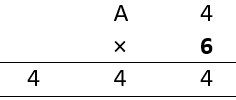
To satisfy this condition, A × 6 must become 42. Which is possible for A = 7.
For B = 6,
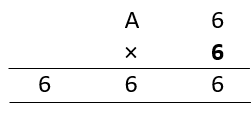
To satisfy this condition, A × 6 must become 63. Which is not possible.
For B = 8,
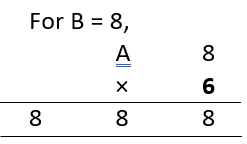
To satisfy this condition, A × 6 must become 84. Which is possible for A = 14. As we need only one-digit number. So, we can’t accept this value of A.
So, A = 7 and B = 4 will satisfy this Question.
8)
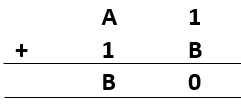
Sol.: – B can be between 0 to 9. But to make 1 + B = 0, only accepted value of B is 9. So, 1 + 9 = 10.
Now we must make 1 + A + 1 = B. Since B = 9, A becomes 7.
So, A = 7 and B = 9 will satisfy this Question.
9)
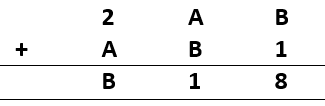
Sol.: – B can be between 0 to 9. But to make B + 1 = 8, only accepted value of B is 7.
Also, A + B = 1, and here B = 7. So, A becomes 4.
Which satisfy last line 1 + 2 + A = B i.e. 1 + 2 + 4 = 7.
So, A = 4 and B = 7 will satisfy this Question.
10)
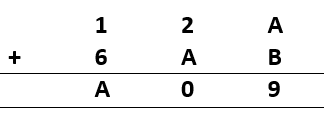
Sol.: – It Is shown that, 2 + A = 0, which can only mean 2 + A = 10. So, value of A = 8.
And A + B = 9. Putting A = 8, we get B = 1.
It satisfies all conditions.
So, A = 8 and B = 1 will satisfy this Question.
The next Exercise for NCERT Solutions for Class 8 Maths Chapter 16 Exercise 16.2 – Playing with Numbers can be accessed by clicking here
Download NCERT Solutions for Class 8 Maths Chapter 16 Exercise 16.1 – Playing with Numbers

