Arinjay Academy » Maths Class 8 » NCERT Solutions for Class 8 Maths Chapter 1 Exercise 1.2 Rational Numbers

NCERT Solutions for Class 8 Maths Chapter 1 Exercise 1.2 Rational Numbers

NCERT Solutions for Class 8 Maths Chapter 1 Exercise 1.2 , has been designed by the NCERT to test the knowledge of the student on the following topics :

Representation of Rational Numbers on the Number Line
Rational Numbers between Two Rational Numbers

NCERT Solutions for Class 8 Maths Chapter 1 Exercise 1.2 Rational Numbers

NCERT Solutions for Class 8 Maths Chapter 1 Exercise 1.2 Rational Numbers

1.1 Introduction

Q.1 Represent these numbers on the number line.
(i) $\cfrac { 7 }{ 4 }$
(ii) $\cfrac { -5 }{ 6 }$

Solution:

(i) Representing $\cfrac { 7 }{ 4 }$ on number line : –

We take 7 markings at a distance $\cfrac { 1 }{ 4 }$ each on the right of zero and starting from zero (The number of markings required to be taken are equal to the value of the numerator, , i.e, 7 in this case) . The seventh marking is $\cfrac { 7 }{ 4 }$

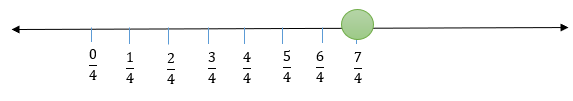
(ii) Representing $\cfrac { -5 }{ 6 }$ on number line:

We make 5 markings at a distance $\cfrac { 1 }{ 6 }$ each on the left of zero and starting from zero (The number of markings required to be taken are equal to the value of the numerator, i.e, 5 in this case ). The fifth marking is $\cfrac { -5 }{ 6 }$

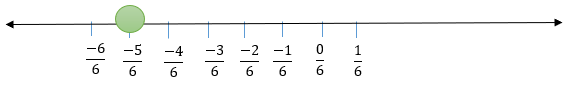
Q.2 Represent $\cfrac { -2 }{ 11 }$ , $\cfrac { -5 }{ 11 }$ , $\cfrac { -9 }{ 11 }$ on the number line.

Solution:

We make 11 markings at a distance $\cfrac { 1 }{ 11 }$ each on the left of zero and starting from zero. The second marking is $\cfrac { -2 }{ 11 }$ the fifth marking is $\cfrac { -5 }{ 11 }$ and the ninth marking is $\cfrac { -9 }{ 11 }$

Q.3 Write five rational numbers which are smaller than 2.

Solution:

2 can be represented as $\cfrac { 10 }{ 5 }$
Five rational numbers smaller than 2 are $\cfrac { 9}{ 5 }$ , $\cfrac { 8 }{ 5 }$ , $\cfrac { 7 }{ 5 }$ , $\cfrac { 6 }{ 5 }$ , $\cfrac { 5 }{ 5 }$

Q.4 Find ten rational numbers between $\cfrac { -2 }{ 5 }$ and $\cfrac { 1 }{ 2 }$

Solution:

$\cfrac { -2 }{ 5 }$ can also be written as $\cfrac { -8 }{ 20 }$ and $\cfrac { 1 }{ 2 }$ can also be written as $\cfrac { 10 }{ 20 }$
So, any ten rational numbers lying between $\cfrac { -8 }{ 10 }$ , $\cfrac { 10 }{ 20 }$ are ten rational numbers between $\cfrac { -2 }{ 5 }$ and $\cfrac { 1 }{ 2 }$
Therefore, ten rational numbers between $\cfrac { -2 }{ 5 }$ and $\cfrac { 1 }{ 2 }$
$\cfrac { -7 }{ 20 }$ , $\cfrac { -6 }{ 20 }$ , $\cfrac { -5 }{ 20 }$ , $\cfrac { -4 }{ 20 }$ , $\cfrac { -3 }{ 20 }$ , $\cfrac { -2 }{ 20 }$ , $\cfrac { -1 }{ 20 }$ , 0, $\cfrac { 1 }{ 20 }$ , $\cfrac { 2 }{ 20 }$
(There can be many more such rational numbers)

Q.5 Find five rational numbers between
(i) $\cfrac { 2 }{ 3 }$ and $\cfrac { 4 }{ 5 }$
(ii) $\cfrac { -3 }{ 2 }$ and $\cfrac { 5 }{ 3 }$
(iii) $\cfrac { 1 }{ 4 }$ and $\cfrac { 1 }{ 2 }$

Solution:

(i) $\cfrac { 2 }{ 3 }$ can be written as $\cfrac { 40 }{ 60 }$ and $\cfrac { 4 }{ 5 }$ can be written as $\cfrac { 48 }{ 60 }$
Therefore, five rational numbers between $\cfrac { 2 }{ 3 }$ and $\cfrac { 4 }{ 5 }$
$\cfrac { 41 }{ 60 }$ , $\cfrac { 42 }{ 60 }$ , $\cfrac { 43 }{ 60 }$ , $\cfrac { 44 }{ 60 }$ , $\cfrac { 45 }{ 60 }$
(There can be many more such rational numbers)

(ii) $\cfrac { -3 }{ 2 }$ can be written as $\cfrac { -9 }{ 6 }$ and $\cfrac { 5 }{ 3 }$ can be written as $\cfrac { 10 }{ 6 }$
Therefore, five rational numbers between $\cfrac { -3 }{ 2 }$ and $\cfrac { 5 }{ 3 }$
$\cfrac { -8 }{ 6 }$ , $\cfrac { -7 }{ 6 }$ , 0, $\cfrac { 1 }{ 6 }$ , $\cfrac { 2 }{ 6 }$
(There can be many more such rational numbers)

(iii) $\cfrac { 1 }{ 4 }$ can be written as $\cfrac { 8 }{ 32 }$ and $\cfrac { 1 }{ 2 }$ can be written as $\cfrac { 1 }{ 6 }$
Therefore, five rational numbers between $\cfrac { 1 }{ 4 }$ and $\cfrac { 1 }{ 2 }$
$\cfrac { 9 }{ 32 }$ , $\cfrac { 10 }{ 32 }$ , $\cfrac { 11 }{ 32 }$ , $\cfrac { 12 }{ 32 }$ , $\cfrac { 13 }{ 32 }$
(There can be many more such rational numbers)

Q.6 Write five rational numbers greater than -2

Solution:

-2 can also be written as $\cfrac { -10 }{ 5 }$
Therefore, five rational numbers greater than -2 are
$\cfrac { -9 }{ 5 }$ , $\cfrac { -8 }{ 5 }$ , $\cfrac { -7 }{ 5 }$ , $\cfrac { -6 }{ 5 }$ , $\cfrac { -5 }{ 5 }$
(There can be many more such rational numbers)

Q.7 Find ten rational numbers between $\cfrac { 3 }{ 5 }$ and $\cfrac { 3 }{ 4 }$

Solution:
$\cfrac { 3 }{ 4 }$ can also be written as $\cfrac { 60 }{ 80 }$ and $\cfrac { 3 }{ 5 }$ can also be written as $\cfrac { 48 }{ 80 }$
Therefore, ten rational numbers between $\cfrac { 3 }{ 5 }$ and $\cfrac { 3 }{ 4 }$
$\cfrac { 49 }{ 80 }$ , $\cfrac { 50 }{ 80 }$ , $\cfrac { 51 }{ 80 }$ , $\cfrac { 52 }{ 80 }$ , $\cfrac { 53 }{ 80 }$ , $\cfrac { 54 }{ 80 }$ , $\cfrac { 55 }{ 80 }$ , $\cfrac { 56 }{ 80 }$ , $\cfrac { 57 }{ 80 }$ , $\cfrac { 58 }{ 80 }$
(There can be many more such rational numbers)

The next Exercise for NCERT Solutions for Class 8 Maths Chapter 2 Exercise 2.1 – Linear Equation in two Variables can be accessed by clicking here .

NCERT Solutions for Class 8 Maths Chapter 1 Exercise 1.2 – Rational Numbers

NCERT Solutions for Class 8 Maths Chapter 1 Exercise 1.2 Rational Numbers

NCERT Solutions for Class 8 Maths Chapter 1 Exercise 1.2 Rational Numbers

NCERT Solutions for Class 8

CBSE Notes for Class 8

Worksheets for Class 8

Leave a Comment Cancel reply