NCERT Solutions for Class 7 Maths Chapter 6 – Triangle and its properties

Class 7 Maths NCERT Solutions Chapter 6 – Triangle and its properties comprises of the 5 Exercises

• Exercise 6.1
• Exercise 6.2
• Exercise 6.3
• Exercise 6.4
• Exercise 6.5

This Chapter contains the Exercises relating to the following topics , which are discussed in Chapter 6 – Triangle and its properties Class 7 NCERT book  : –

• 6.1 INTRODUCTION
• 6.2 MEDIANS OF A TRIANGLE
• 6.3 ALTITUDES OF A TRIANGLE
• 6.4 EXTERIOR ANGLE OF A TRIANGLE AND ITS PROPERTY
• 6.5 ANGLE SUM PROPERTY OF A TRIANGLE
• 6.6 TWO SPECIAL TRIANGLES : EQUILATERAL AND ISOSCELES
• 6.7 SUM OF THE LENGTHS OF TWO SIDES OF A TRIANGLE
• 6.8 RIGHT-ANGLED TRIANGLES AND PYTHAGORAS PROPERTY

NCERT Solutions for Class 7 Maths Chapter 6 Exercise 6.1

NCERT Solutions for Class 7 Maths Chapter 6 Exercise 6.2

NCERT Solutions for Class 7 Maths Chapter 6 Exercise 6.3

NCERT Solutions for Class 7 Maths Chapter 6 Exercise 6.4

NCERT Solutions for Class 7 Maths Chapter 6 Exercise 6.5

NCERT Solutions for Class 7 Maths Chapter 6 Exercise 6.1

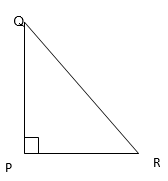
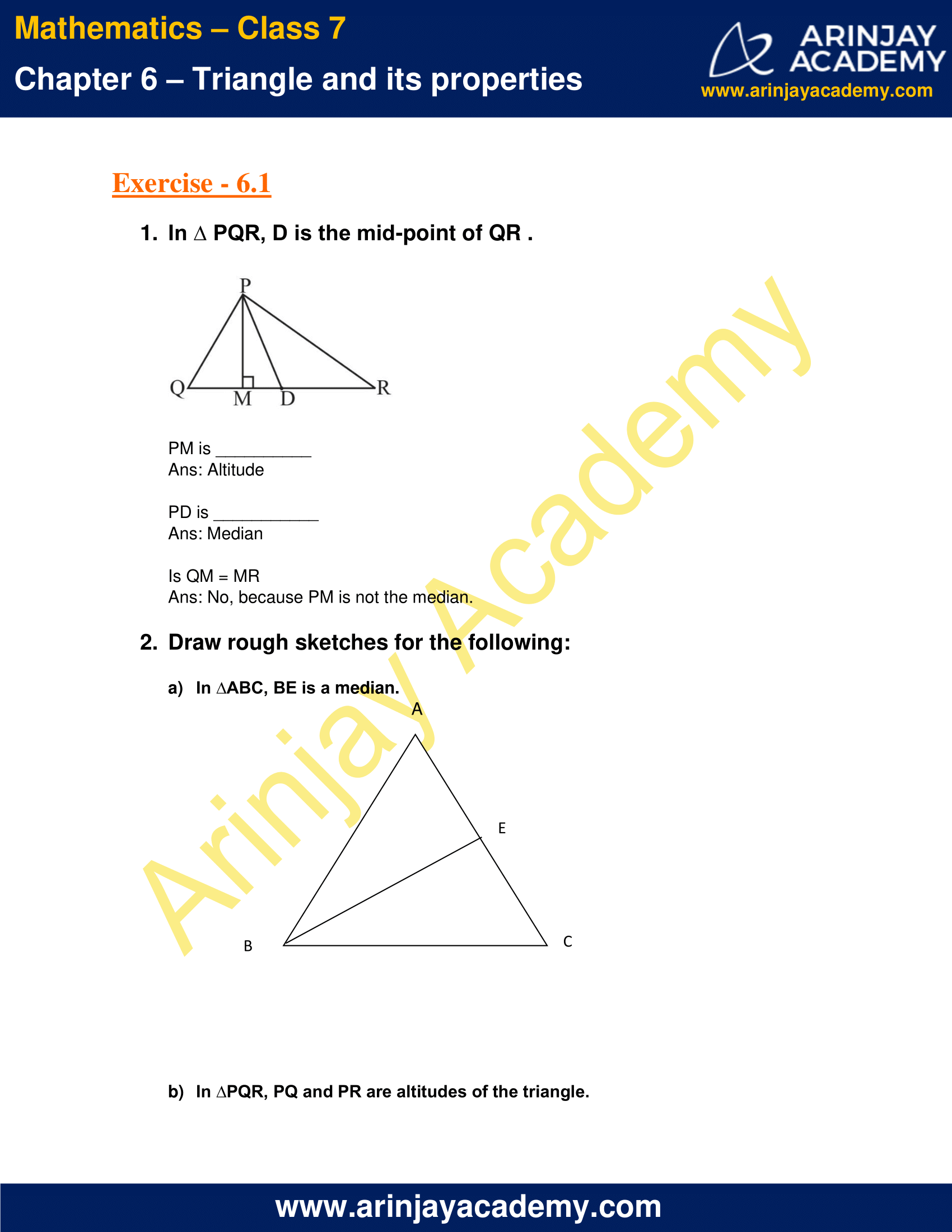
1. In ∆ PQR, D is the mid-point of QR .

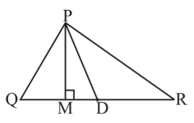
PM is __________
Ans: Altitude

PD is ___________
Ans: Median

Is QM = MR
Ans: No, because PM is not the median.

2. Draw rough sketches for the following:

a) In ∆ABC, BE is a median.

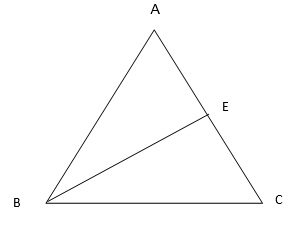
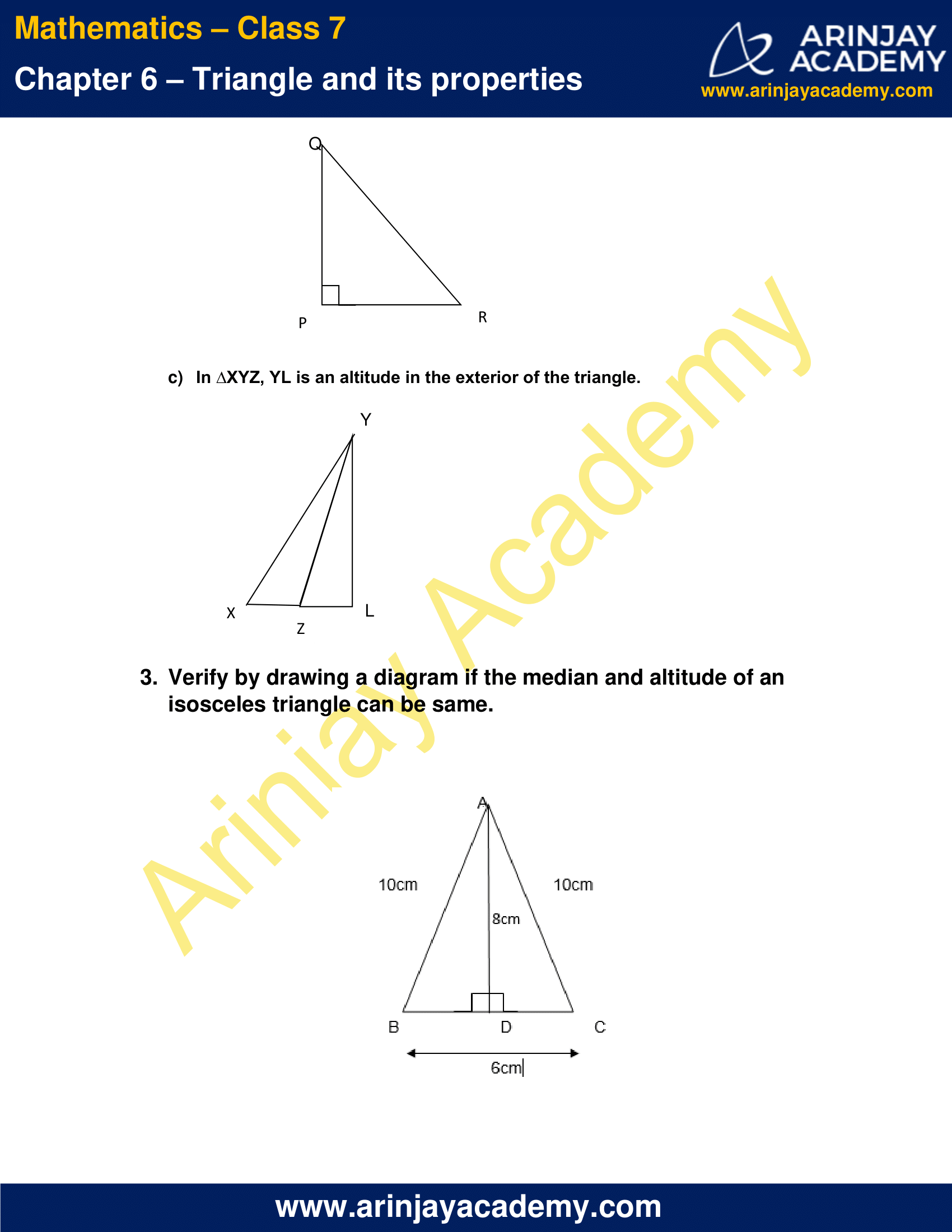
b) In ∆PQR, PQ and PR are altitudes of the triangle.

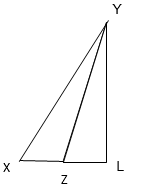
c)  In ∆XYZ, YL is an altitude in the exterior of the triangle.

3. Verify by drawing a diagram if the median and altitude of an isosceles triangle can be same.

NCERT Solutions for Class 7 Maths Chapter 6 Exercise 6.2

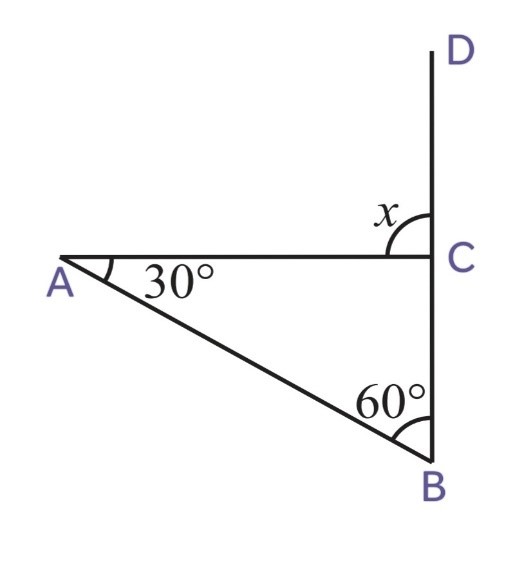
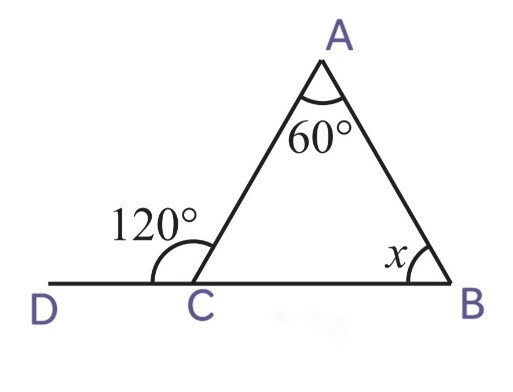
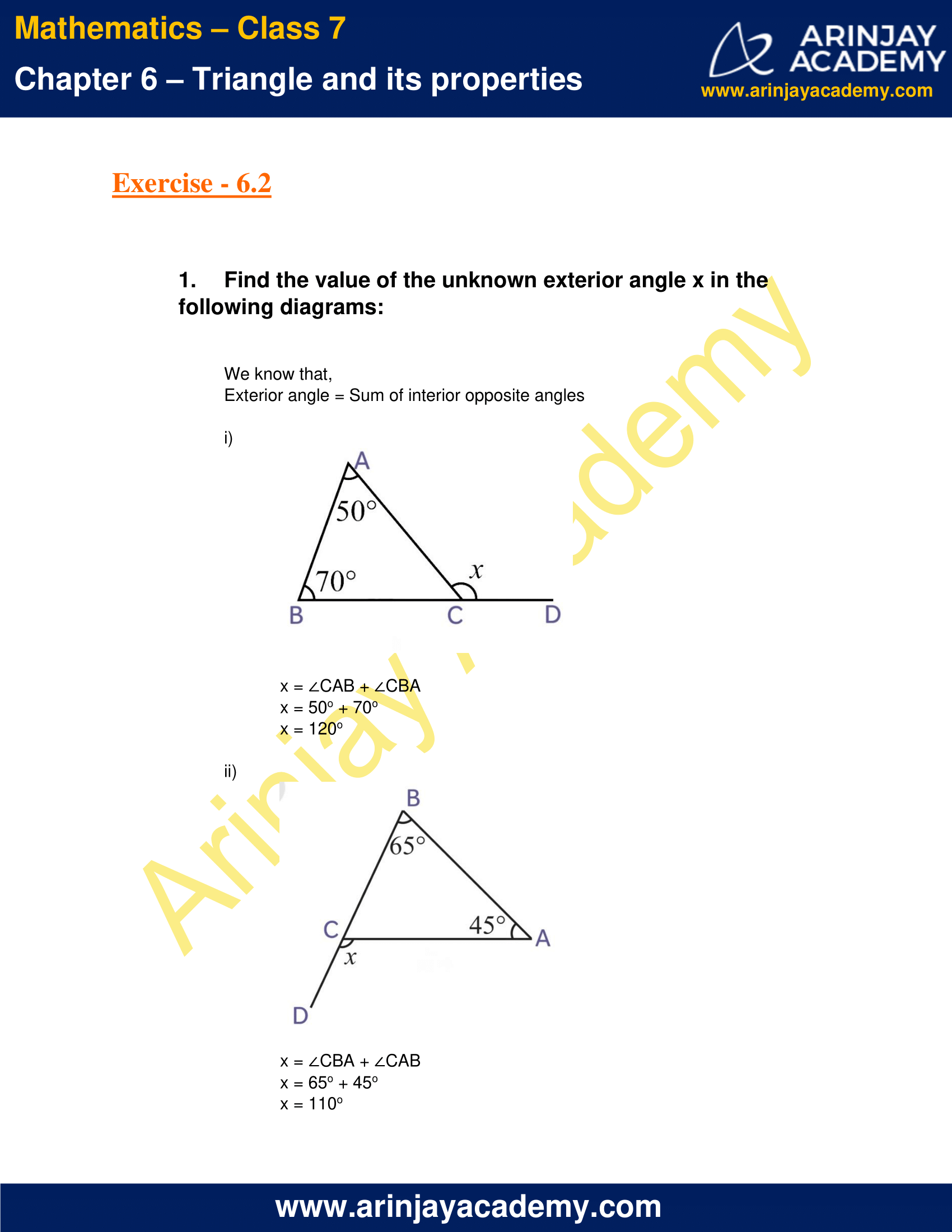
1. Find the value of the unknown exterior angle x in the following diagrams:

We know that,
Exterior angle = Sum of interior opposite angles

(i)

x = ∠CAB + ∠CBA
x = 50^o + 70^o
x = 120^o

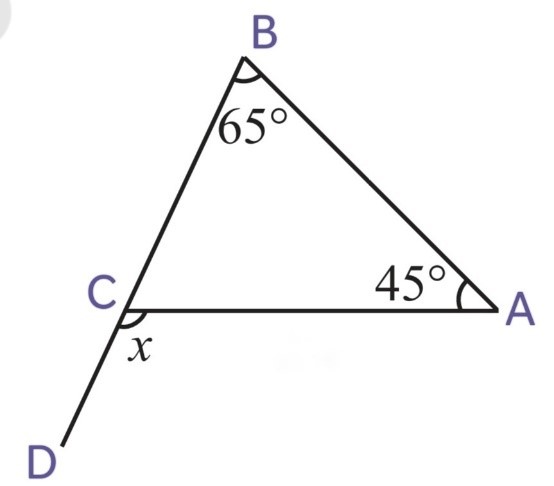
(ii)

x = ∠CBA + ∠CAB
x = 65^o + 45^o
x = 110^o

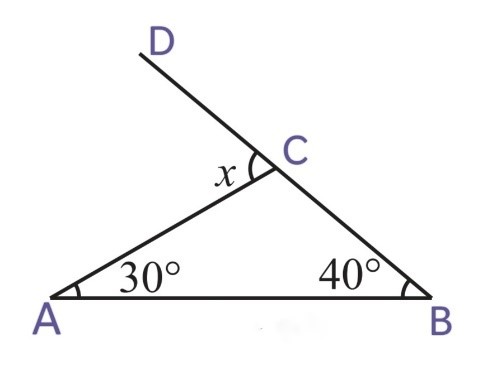
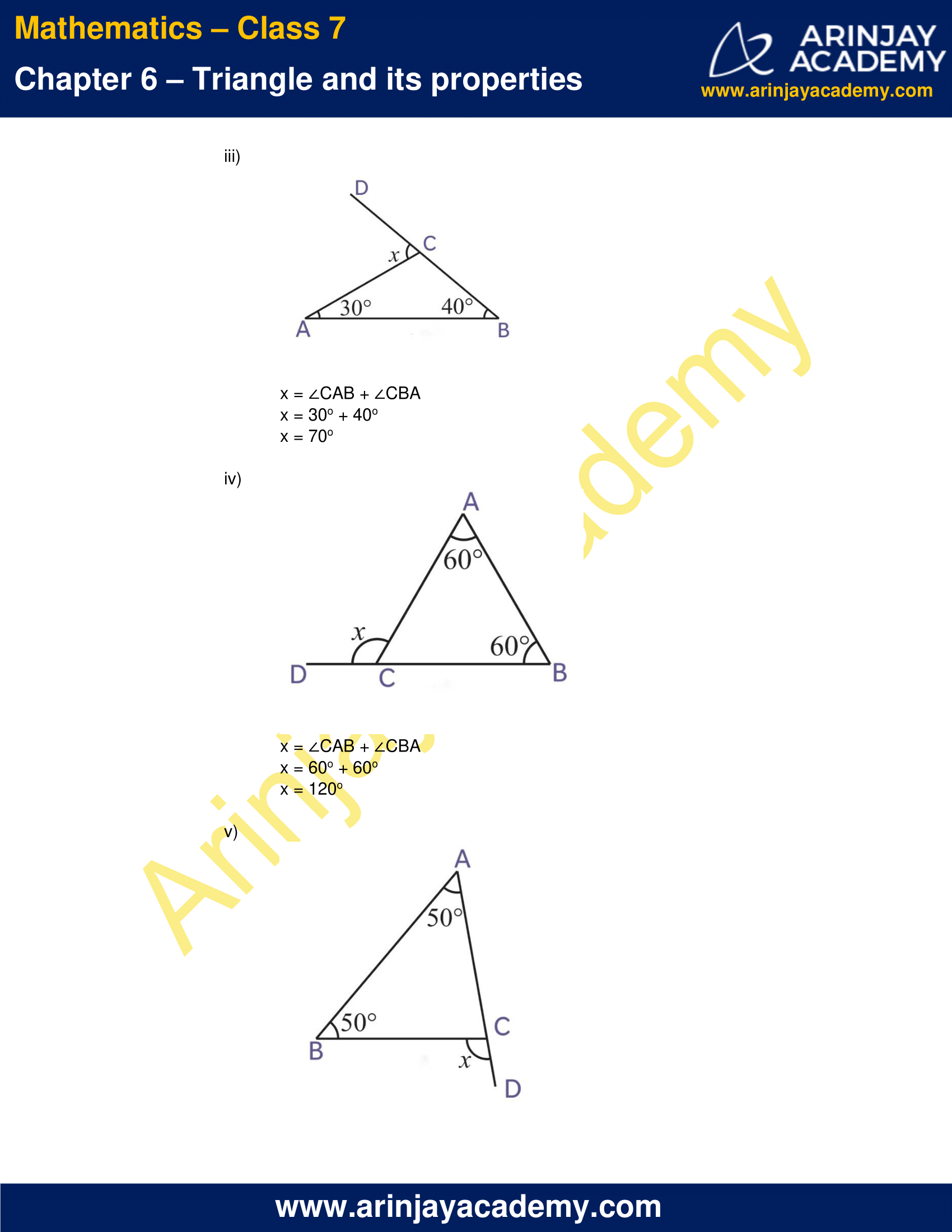
(iii)

x = ∠CAB + ∠CBA
x = 30^o + 40^o
x = 70^o

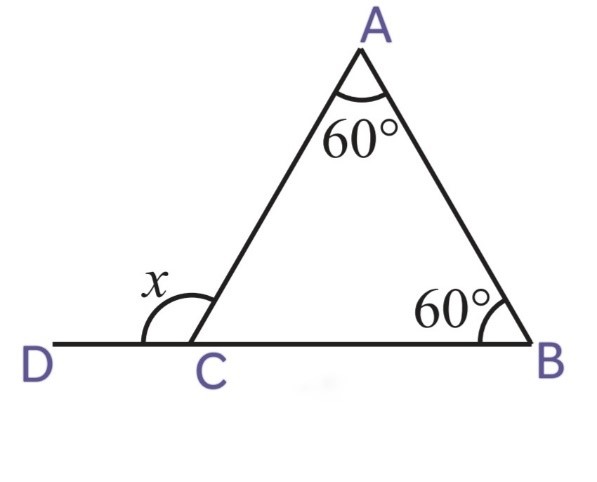
(iv)

x = ∠CAB + ∠CBA
x = 60^o + 60^o
x = 120^o

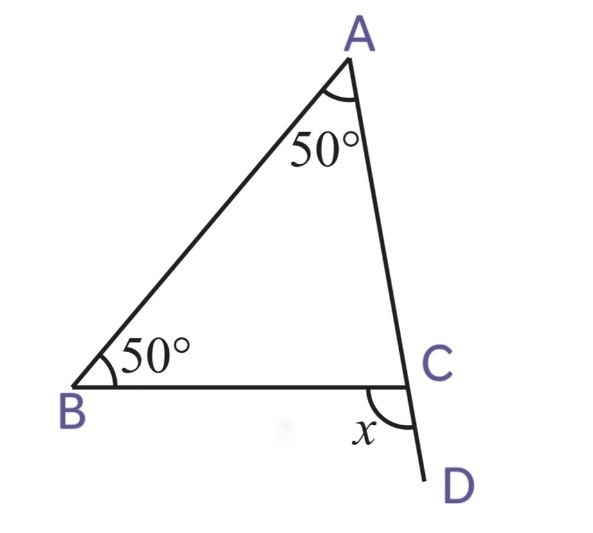
(v) 

x = ∠CAB + ∠CBA
x = 50^o + 50^o
x = 100^o

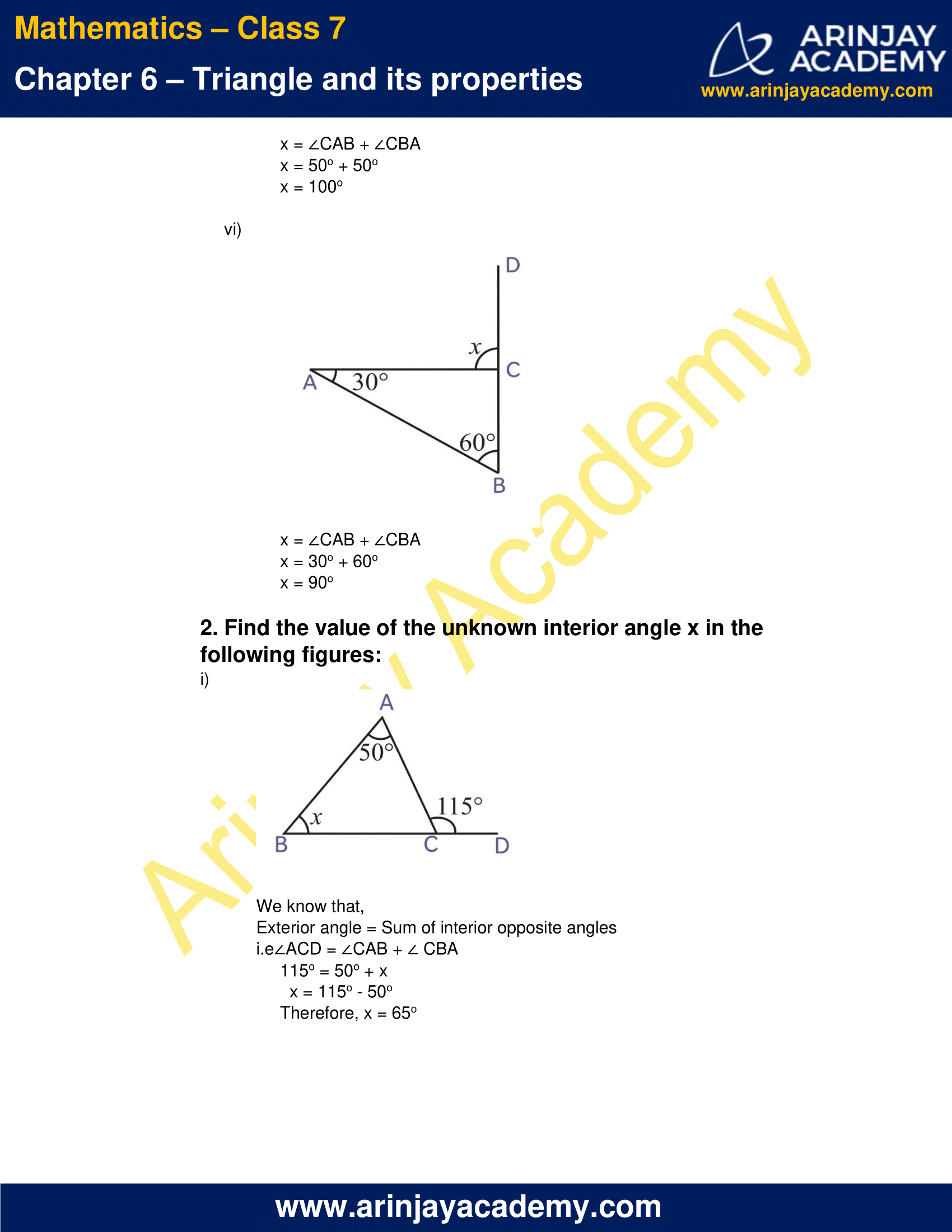
(vi) 

x = ∠CAB + ∠CBA
x = 30^o + 60^o
x = 90^o

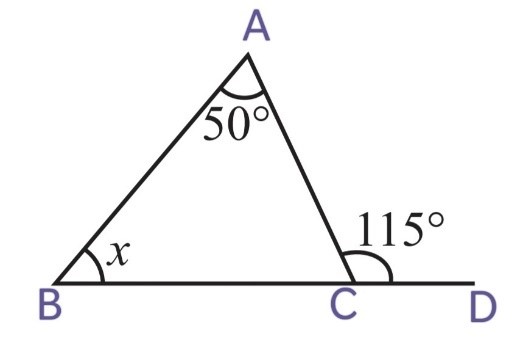
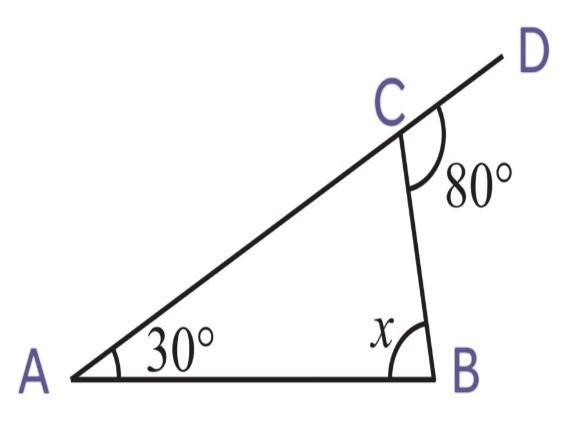
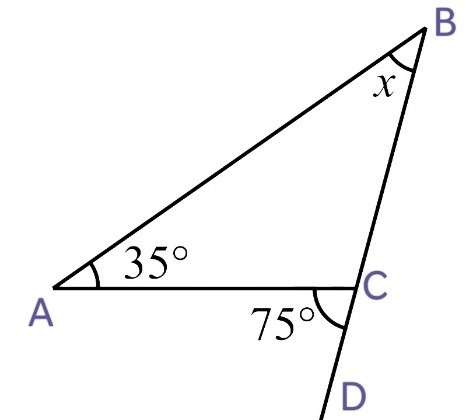
2. Find the value of the unknown interior angle x in the following figures:

(i)

We know that,
Exterior angle = Sum of interior opposite angles
i.e ∠ACD = ∠CAB + ∠ CBA
115^o = 50^o + x
x = 115^o – 50^o
Therefore, x = 65^o

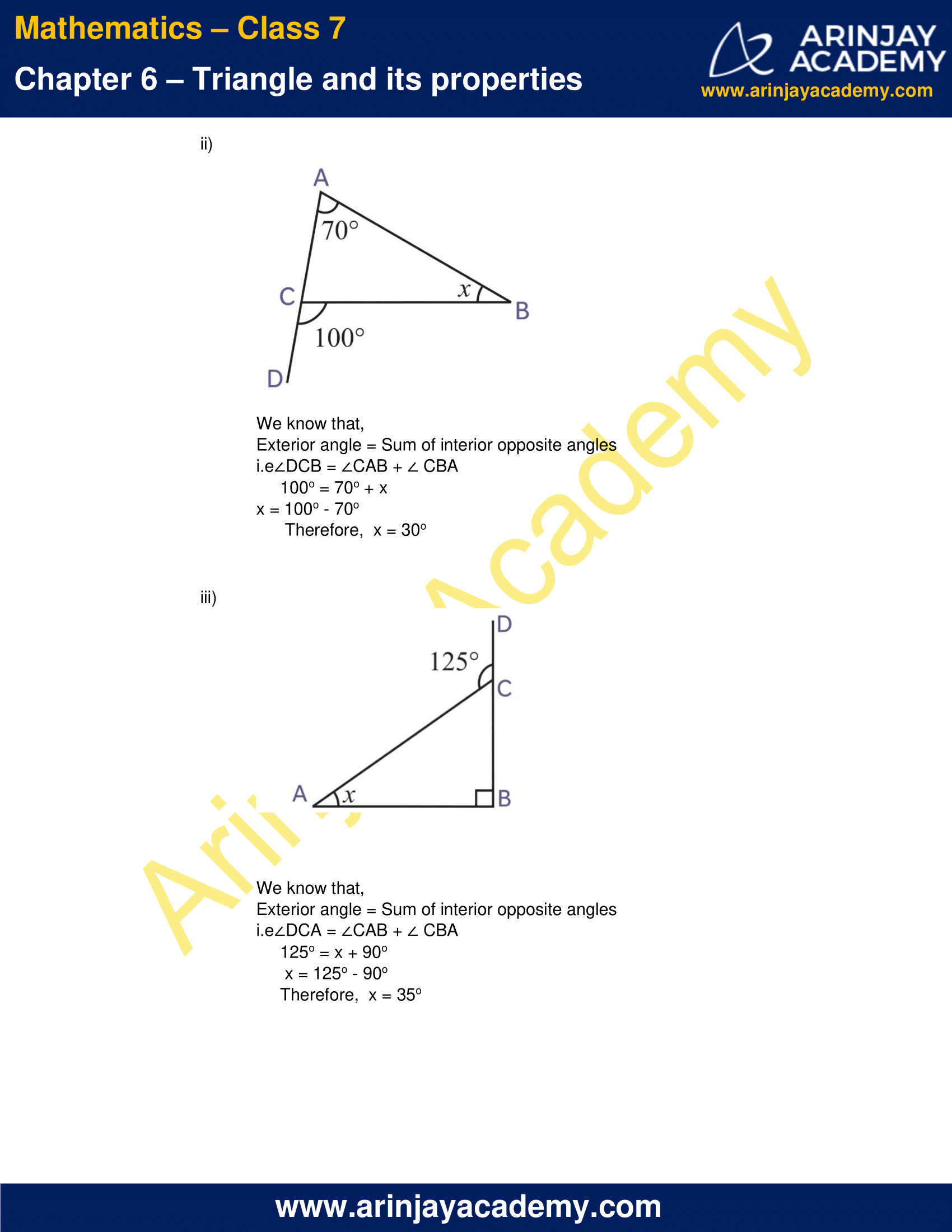
(ii) 

We know that,
Exterior angle = Sum of interior opposite angles
i.e ∠DCB = ∠CAB + ∠ CBA
100^o = 70^o + x
x = 100^o – 70^o
Therefore,  x = 30^o

(iii)

We know that,
Exterior angle = Sum of interior opposite angles
i.e ∠DCA = ∠CAB + ∠ CBA
125^o = x + 90^o
x = 125^o – 90^o
Therefore,  x = 35^o

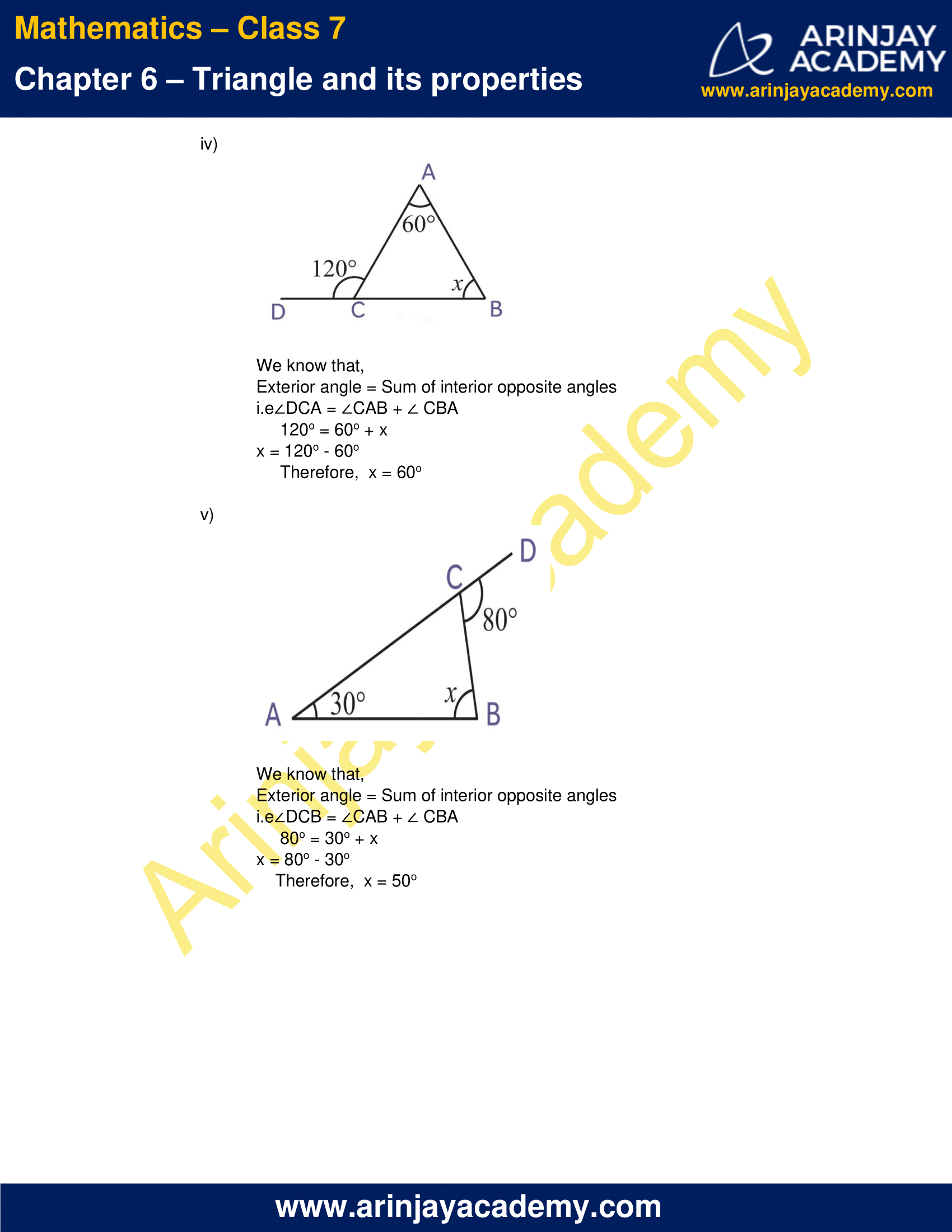
(iv)

We know that,
Exterior angle = Sum of interior opposite angles
i.e ∠DCA = ∠CAB + ∠ CBA
120^o = 60^o + x
x = 120^o – 60^o
Therefore,  x = 60^o

(v)

We know that,
Exterior angle = Sum of interior opposite angles
i.e ∠DCB = ∠CAB + ∠ CBA
80^o = 30^o + x
x = 80^o – 30^o
Therefore,  x = 50^o

(vi)

We know that,
Exterior angle = Sum of interior opposite angles
i.e ∠DCA = ∠CAB + ∠ CBA
75^o = 35^o + x
x = 75^o – 35^o
Therefore,  x = 40^o

NCERT Solutions for Class 7 Maths Chapter 6 Exercise 6.3

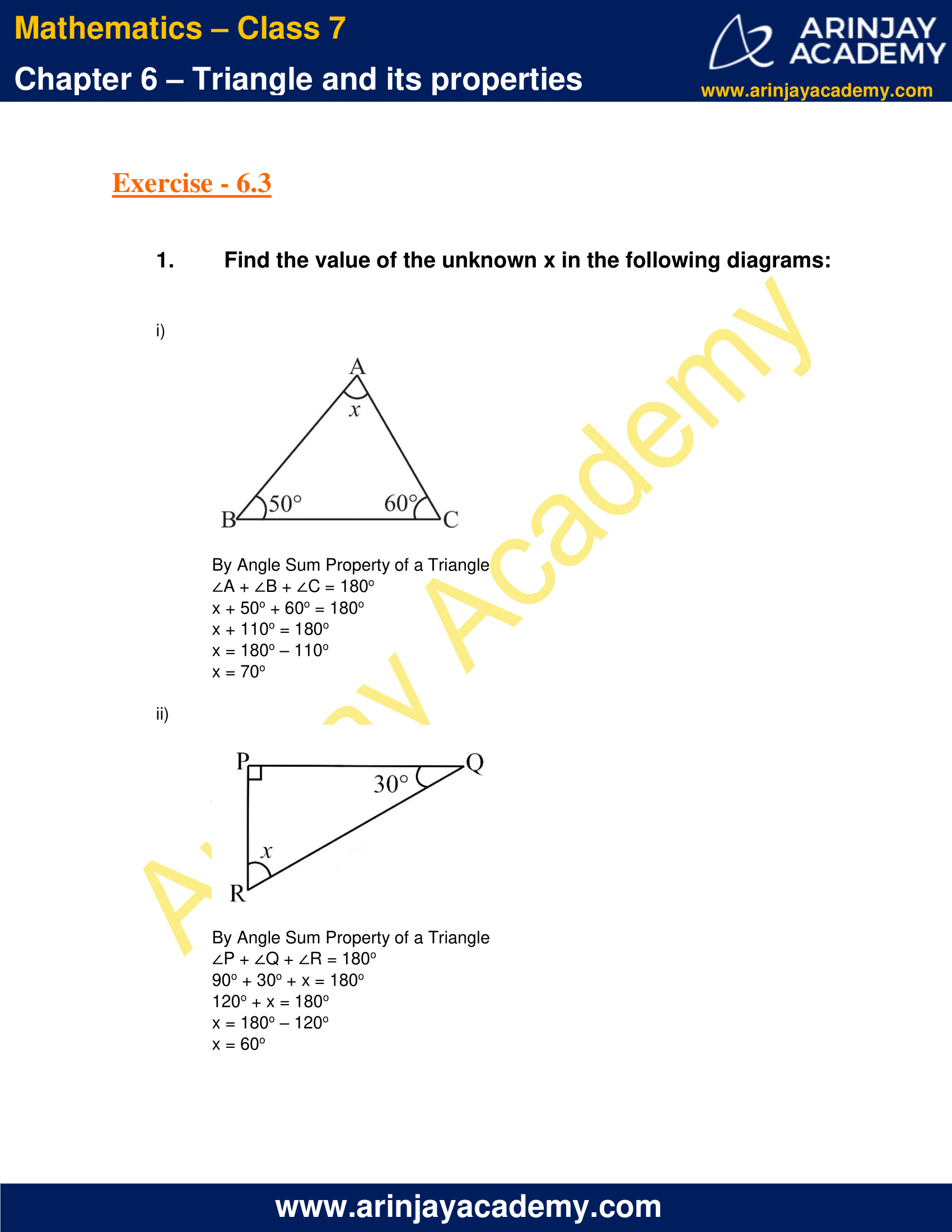
1. Find the value of the unknown x in the following diagrams:

(i)

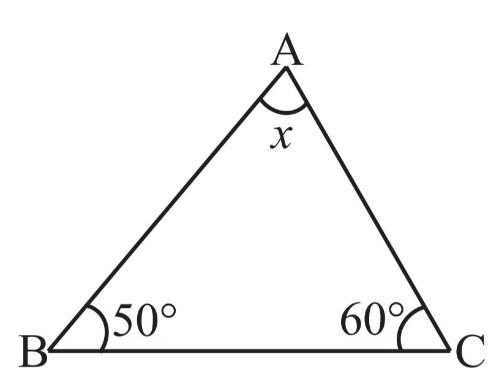
By Angle Sum Property of a Triangle
∠A + ∠B + ∠C = 180^o
x + 50^o + 60^o = 180^o
x + 110^o = 180^o
x = 180^o – 110^o
x = 70^o

(ii)

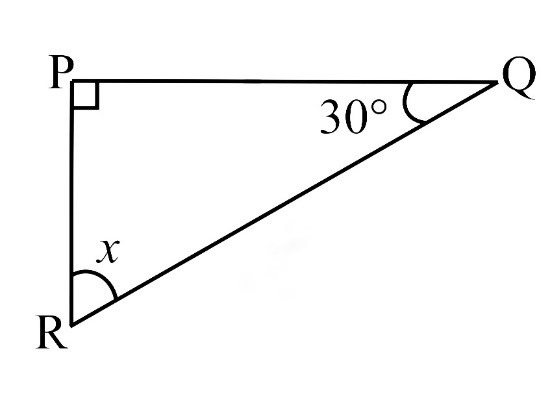
By Angle Sum Property of a Triangle
∠P + ∠Q + ∠R = 180^o
90^o + 30^o + x = 180^o
120^o + x = 180^o
x = 180^o – 120^o
x = 60^o

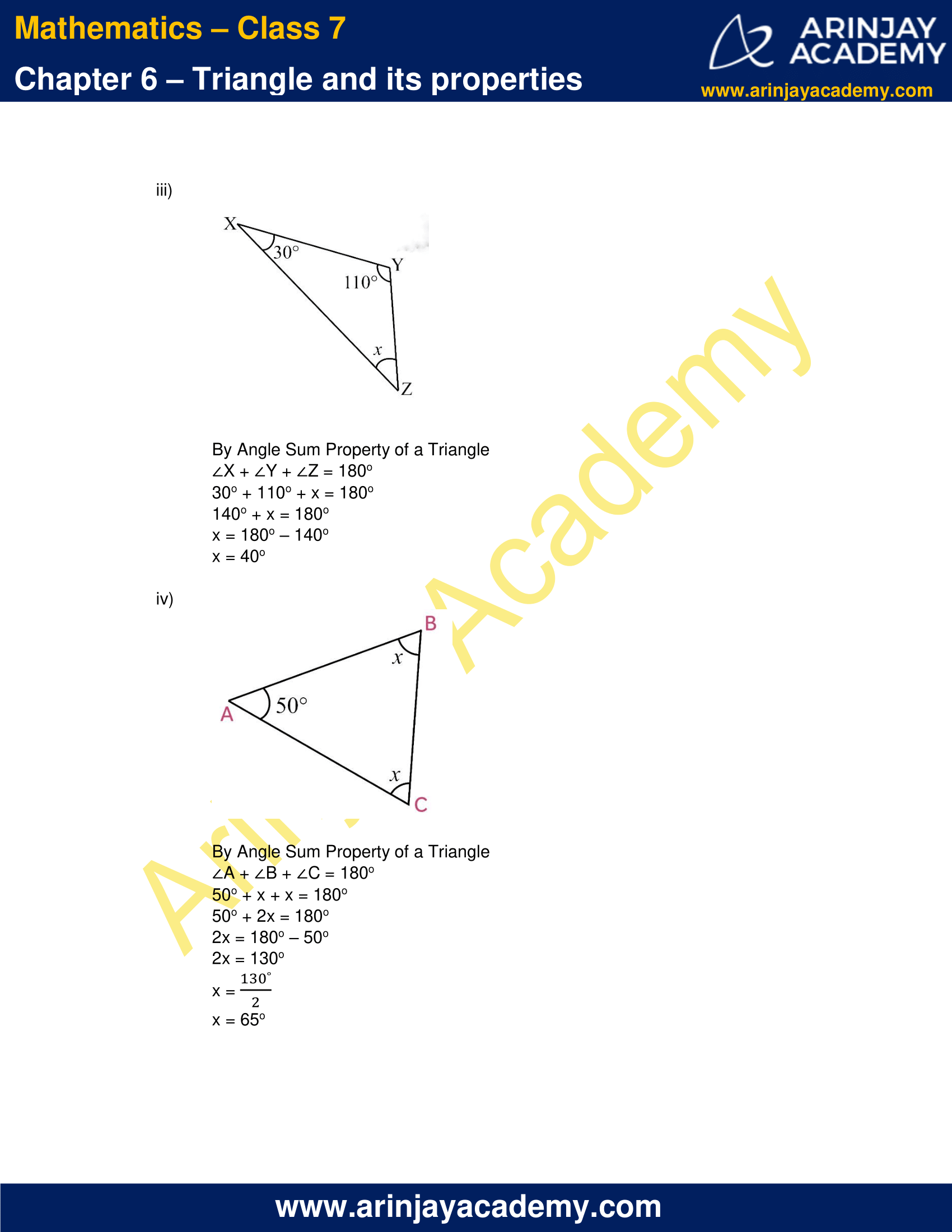
(iii)

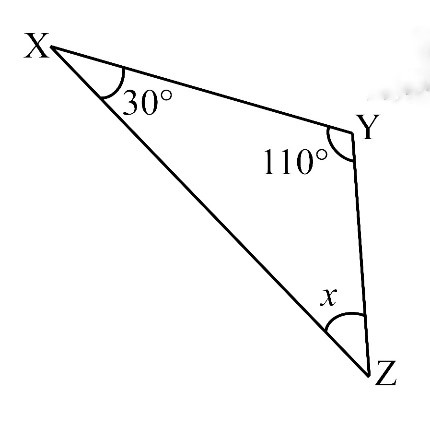
By Angle Sum Property of a Triangle
∠X + ∠Y + ∠Z = 180^o
30^o + 110^o + x = 180^o
140^o + x = 180^o
x = 180^o – 140^o
x = 40^o

(iv)

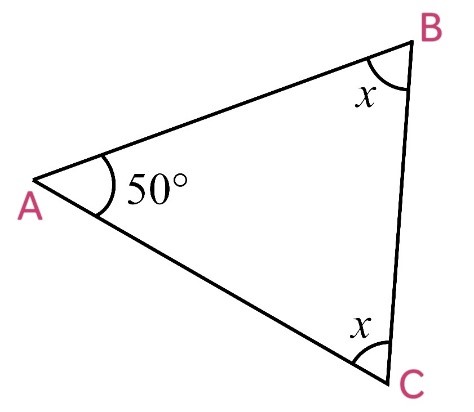
By Angle Sum Property of a Triangle
∠A + ∠B + ∠C = 180^o
50^o + x + x = 180^o
50^o + 2x = 180^o
2x = 180^o – 50^o
2x = 130^o
x = 130^o/2
x = 65^o

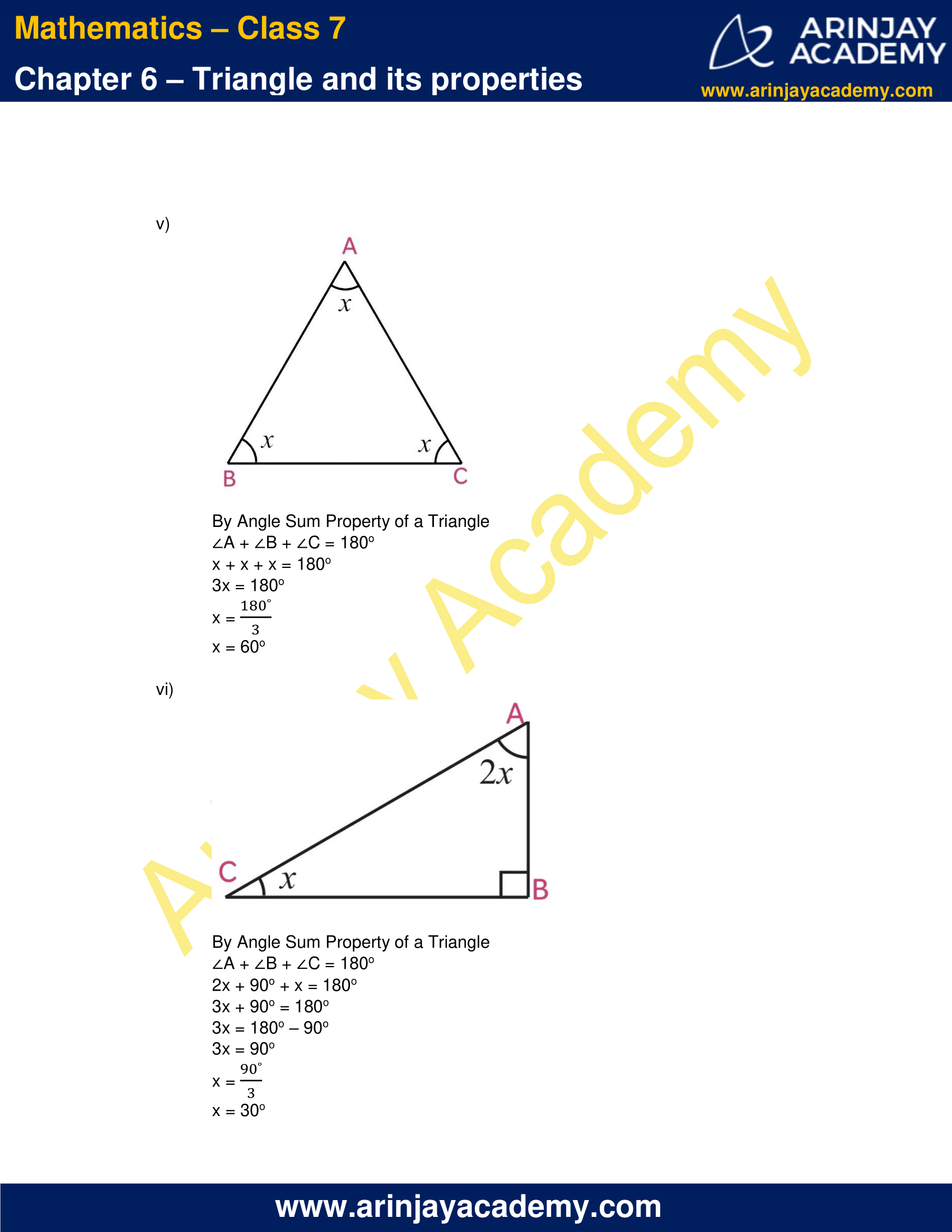
(v)

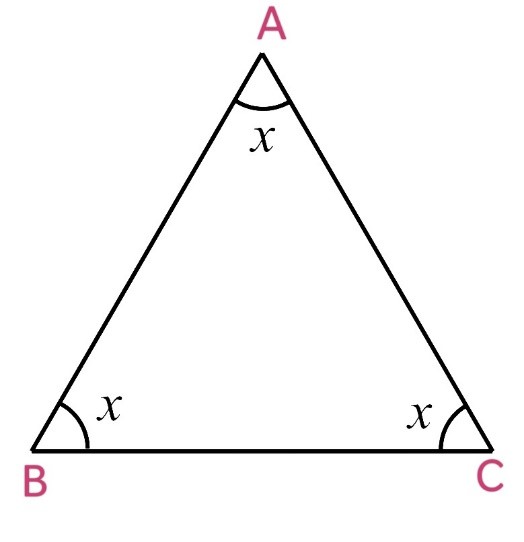
By Angle Sum Property of a Triangle
∠A + ∠B + ∠C = 180^o
x + x + x = 180^o
3x = 180^o
x = 180^o/2
x = 60^o

(vi)

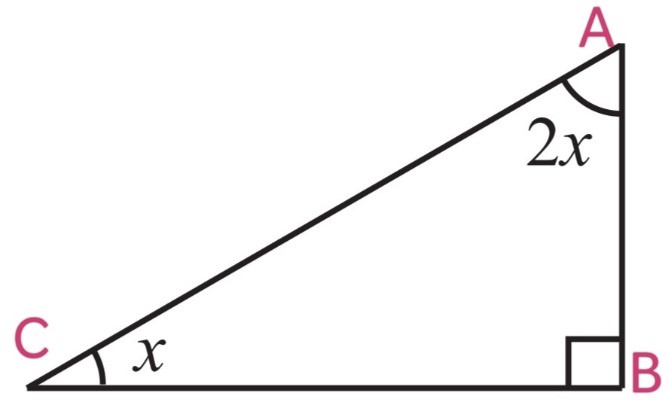
By Angle Sum Property of a Triangle
∠A + ∠B + ∠C = 180^o
2x + 90^o + x = 180^o
3x + 90^o = 180^o
3x = 180^o – 90^o
3x = 90^o
x = 90^o/3
x = 30^o

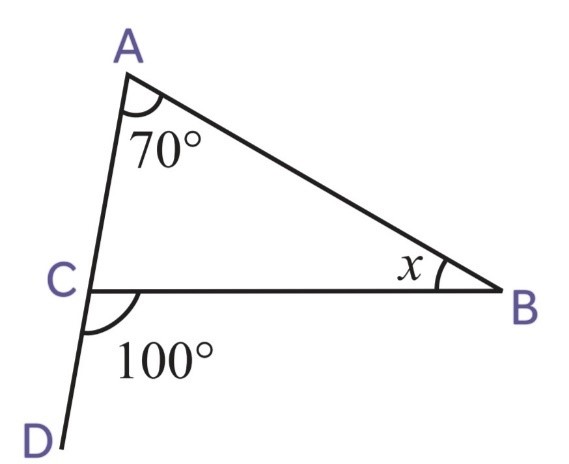
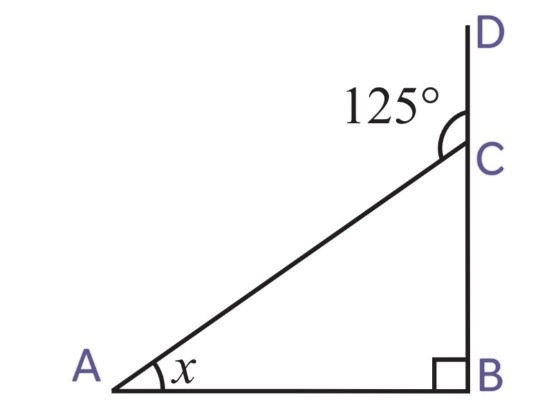
2. Find the values of the unknowns x and y in the following diagrams:

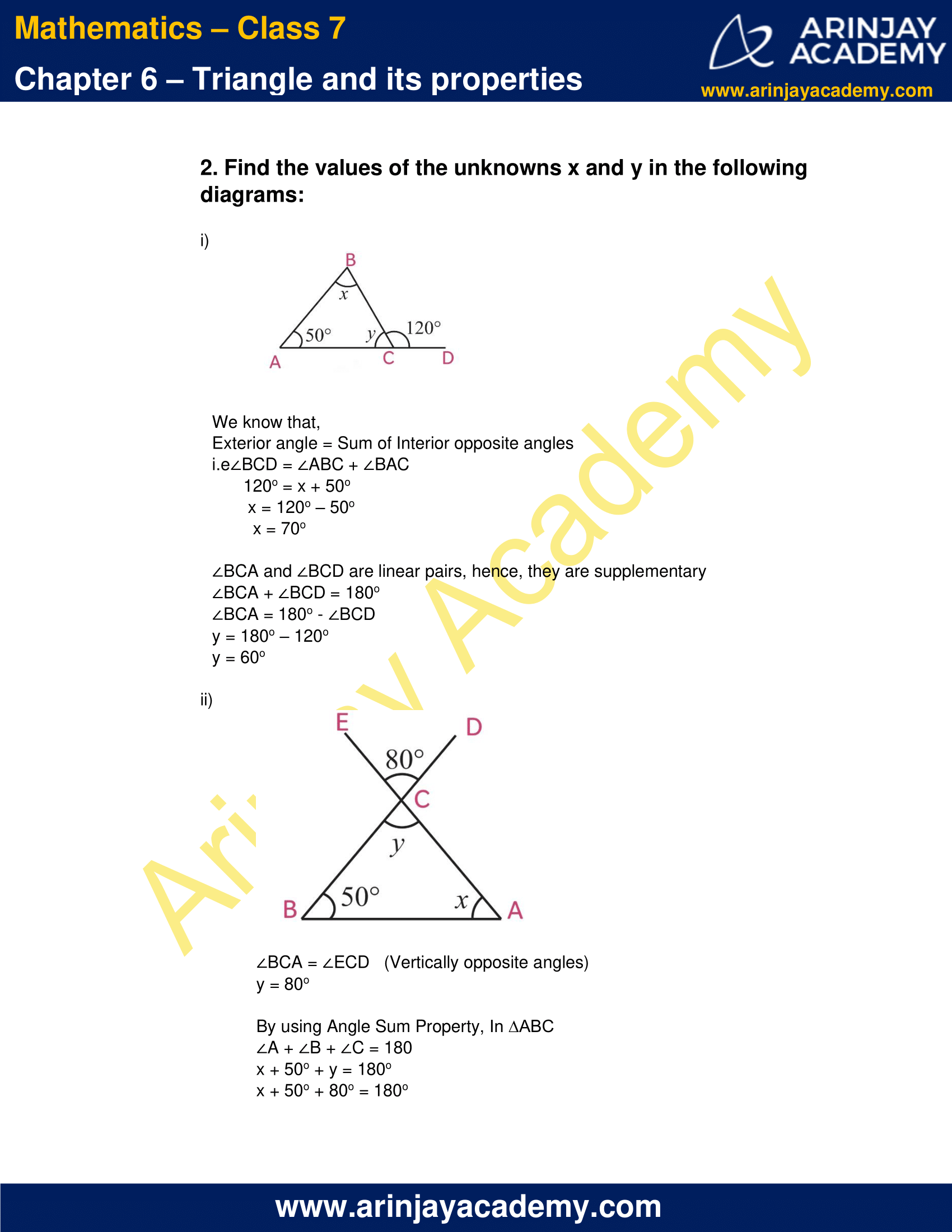
(i)

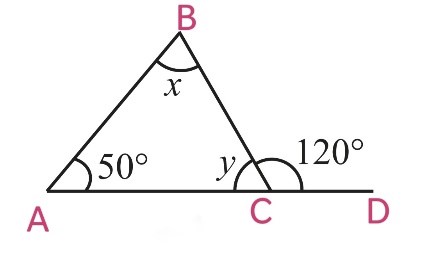
We know that,
Exterior angle = Sum of Interior opposite angles
i.e ∠BCD = ∠ABC + ∠BAC
120^o = x + 50^o
x = 120^o – 50^o
x = 70^o

∠BCA and ∠BCD are linear pairs, hence, they are supplementary
∠BCA + ∠BCD = 180^o
∠BCA = 180^o – ∠BCD
y = 180^o – 120^o
y = 60^o

(ii)

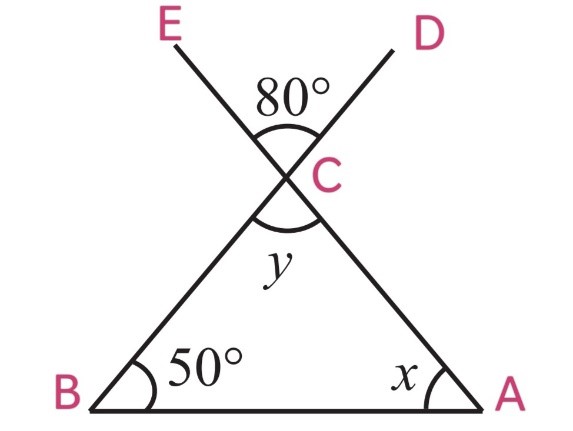
∠BCA = ∠ECD   (Vertically opposite angles)
y = 80^o

By using Angle Sum Property, In ∆ABC
∠A + ∠B + ∠C = 180
x + 50^o + y = 180^o
x + 50^o + 80^o = 180^o
x + 130^o = 180^o
x = 180^o – 130^o
x = 50^o

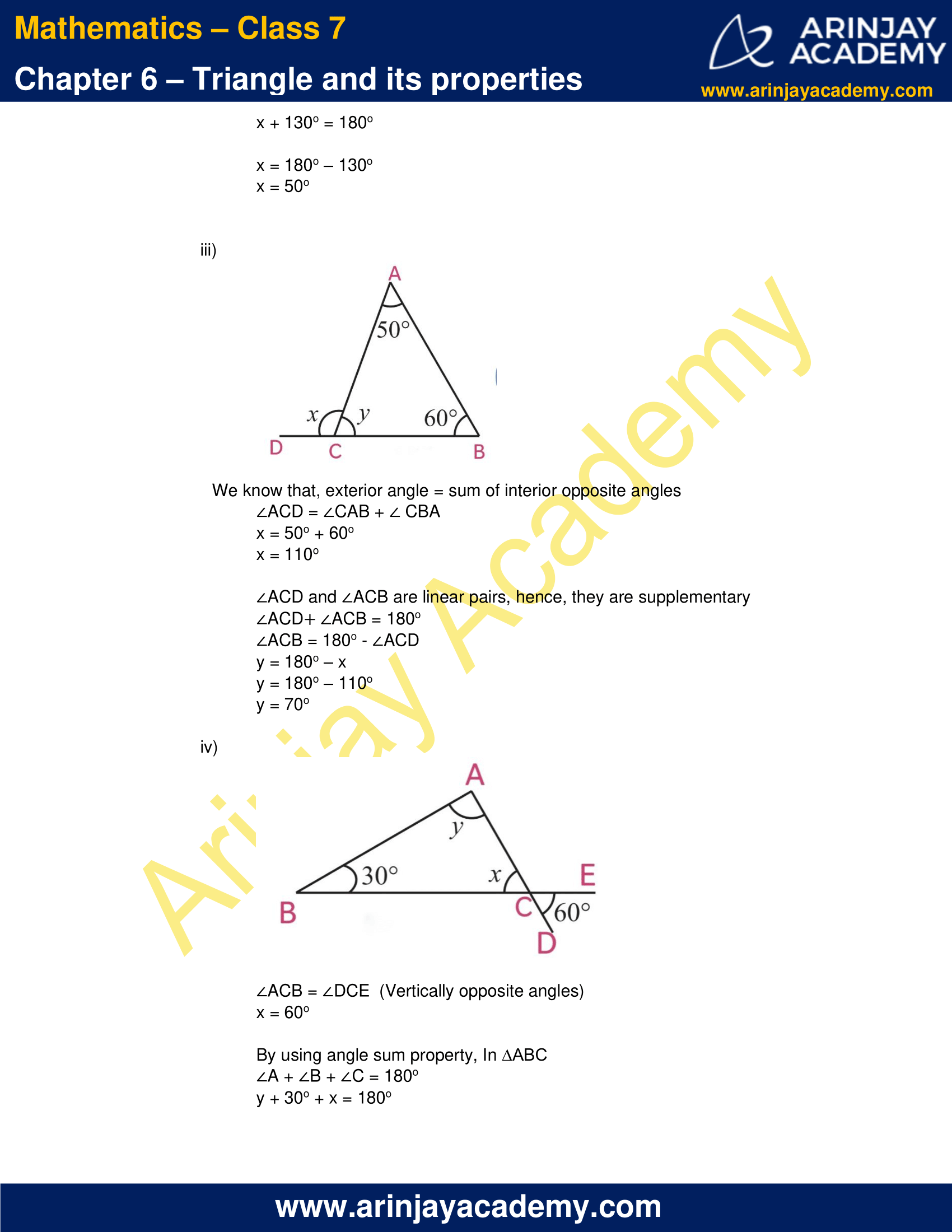
(iii)

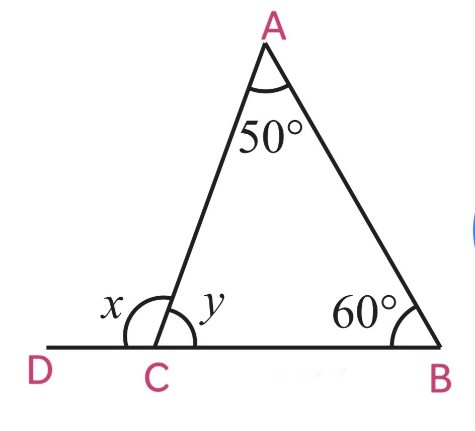
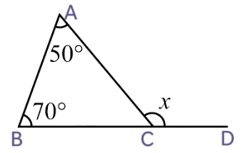
We know that, exterior angle = sum of interior opposite angles
∠ACD = ∠CAB + ∠ CBA
x = 50^o + 60^o
x = 110^o

∠ACD and ∠ACB are linear pairs, hence, they are supplementary
∠ACD + ∠ACB = 180^o
∠ACB = 180^o – ∠ACD
y = 180^o – x
y = 180^o – 110^o
y = 70^o

(iv)

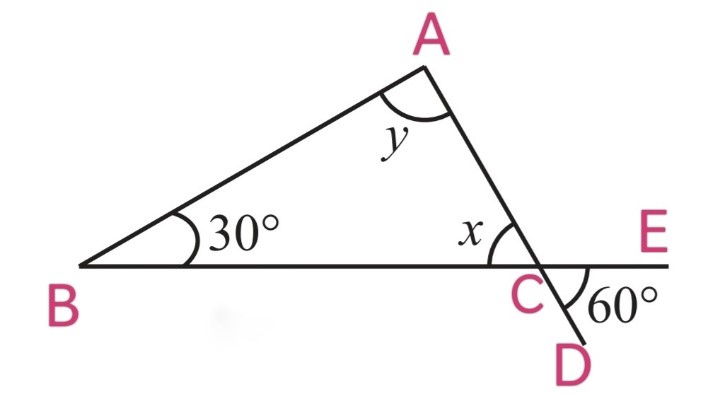
∠ACB = ∠DCE  (Vertically opposite angles)
x = 60^o

By using angle sum property, In ∆ABC
∠A + ∠B + ∠C = 180^o
y + 30^o + x = 180^o
y + 30^o + 60^o = 180^o
y + 90^o = 180^o
y = 180^o – 90^o
y = 90^o

(v)

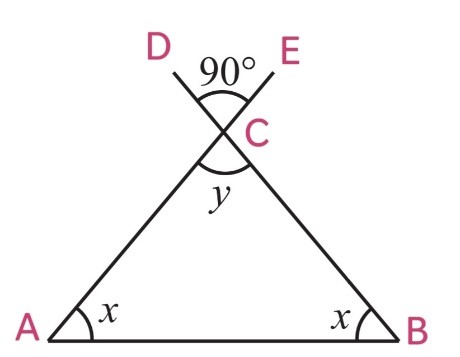
∠ACB = ∠DCE  (Vertically opposite angles)
y = 90^o

By using angle sum property, In ∆ABC
∠A + ∠B + ∠C = 180^o
x + x + y = 180^o
2x + y = 180^o
2x + 90^o = 180^o
2x = 180^o – 90^o
2x = 90^o
x = 90^o/2
x = 45^o

(vi)

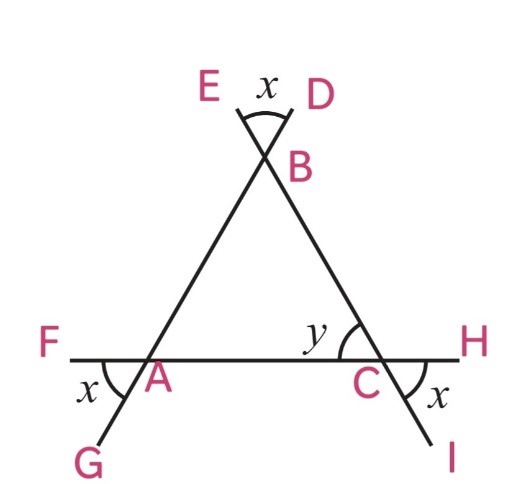
∠ICH = BCA  (Vertically opposite angles)
i.e x = y

Similarly, ∠EBD =∠ABC = x
∠FAG = ∠BAC = x

By using angle sum property, In ∆ABC
∠A + ∠B + ∠C = 180^o
x + x + y = 180^o
x + x + x = 180^o
3x = 180^o
x = 180^o/3
x = 60^o

NCERT Solutions for Class 7 Maths Chapter 6 Exercise 6.4

1. Is it possible to have a triangle with the following sides?

The sum of the lengths of any two sides of a triangle should be greater than the third side.

ii) 3cm, 6cm, 7cm
6cm + 3cm = 9cm > 7cm
6cm + 7cm = 13cm > 3cm
7cm + 3cm = 10cm > 6cm
Hence, this triangle is possible.

2. Take any point O in the interior of a triangle PQR. Is

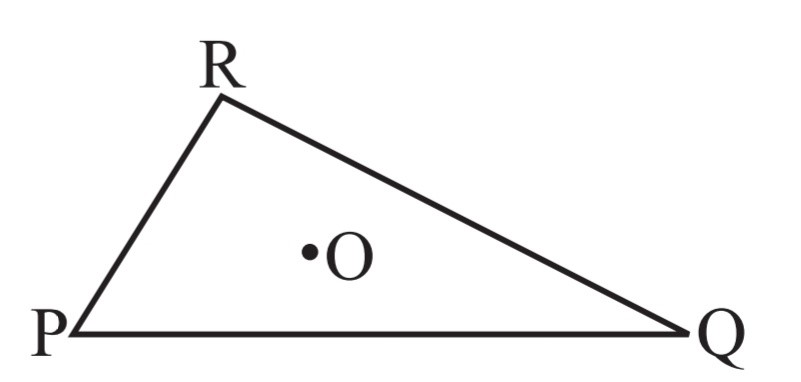
If O is a point in the interior of the triangle ∆PRQ, then, we can construct three triangles ∆OPR, ∆OPQ and ∆ORQ
In a triangle, the sum of the lengths of any two sides is greater than the third side.

i) OP + OQ > PQ?
Yes

ii) OQ + OR > QR?
Yes

iii) OR + OP > RP?
Yes

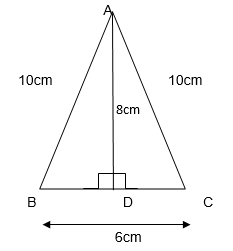
3. AM is a median of a triangle ABC.
Is AB + BC + CA > 2 AM?
(Consider the sides of triangles ∆ABM and ∆AMC.)

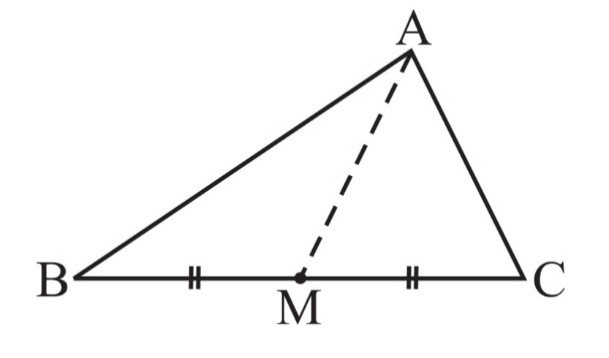
In a triangle, the sum of the lengths of any two sides is greater than the third side.
Consider ∆ABM
AB + BM > AM…… (i)
Consider ∆AMC
CA + CM > AM…. (ii)
Add equation (i) and (ii)
AB + BM + CA + CM > AM + AM
From the figure BM + CM = BC
Therefore AB + BC + CA > 2AM

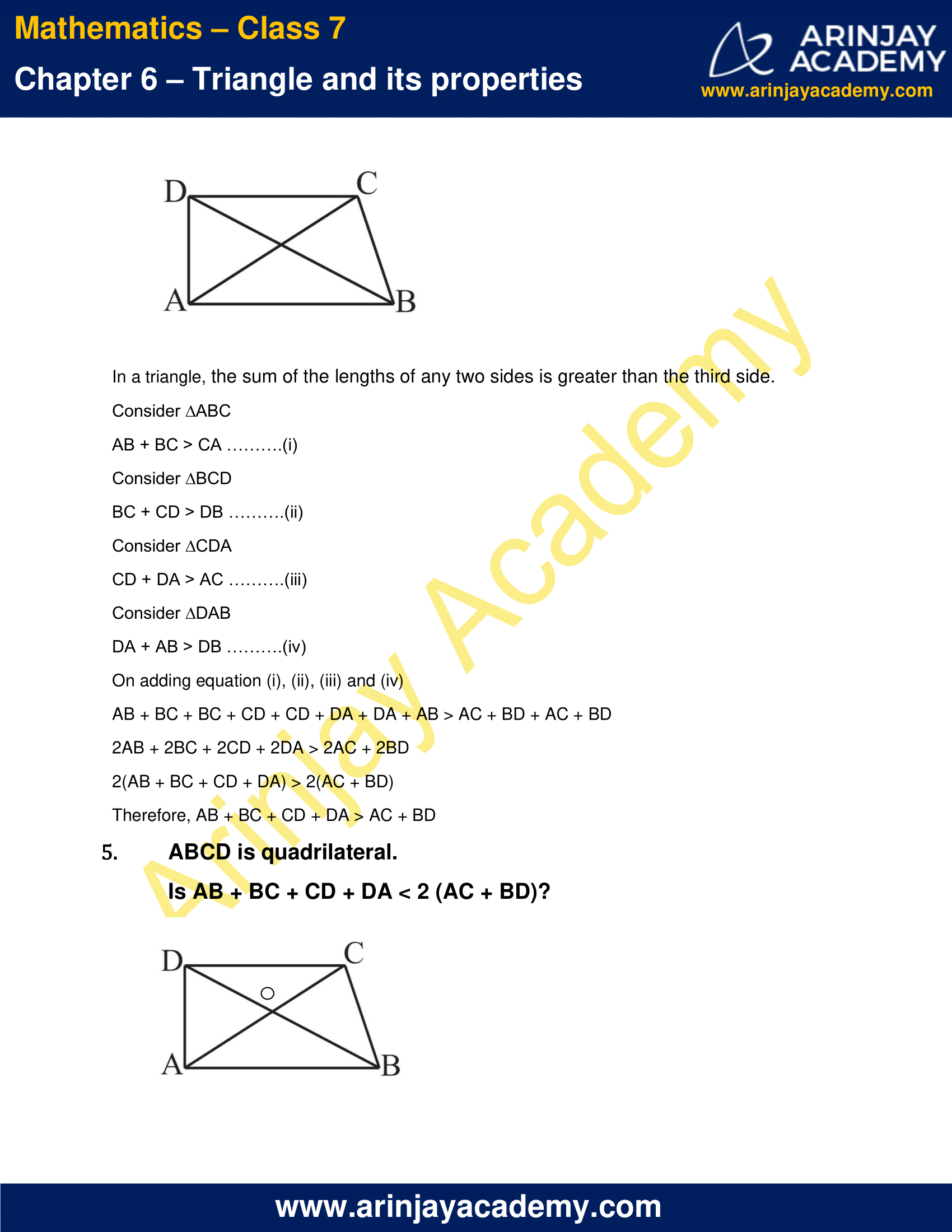
4. ABCD is a quadrilateral.
Is AB + BC + CD + DA > AC + BD?

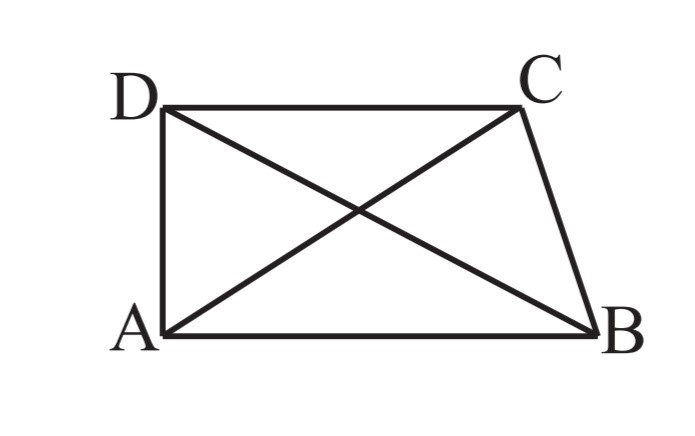
In a triangle, the sum of the lengths of any two sides is greater than the third side.
Consider ∆ABC
AB + BC > CA ….(i)
Consider ∆BCD
BC + CD > DB ….(ii)
Consider ∆CDA
CD + DA > AC ….(iii)
Consider ∆DAB
DA + AB > DB ….(iv)
On adding equation (i), (ii), (iii) and (iv)
AB + BC + BC + CD + CD + DA + DA + AB > AC + BD + AC + BD
2AB + 2BC + 2CD + 2DA > 2AC + 2BD
2(AB + BC + CD + DA) > 2(AC + BD)
Therefore, AB + BC + CD + DA > AC + BD

5. ABCD is quadrilateral.
Is AB + BC + CD + DA < 2 (AC + BD)?

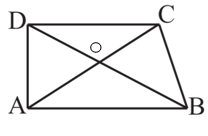
In a triangle, the sum of the lengths of any two sides is greater than the third side.
Consider ∆OAB
OA + OB > AB ….(i)
Consider ∆OBC
OB + OC > BC ….(ii)
Consider ∆OCD
OC + OD > CD ….(iii)
Consider ∆ODA
OD + OA > DA ….(iv)
On adding equation (i), (ii), (iii) and (iv)
OA + OB + OB + OC + OC + OD + OD + OA > AB + BC + CD + DA
2OA + 2OB + 2OC + 2OD > AB +BC + CD + DA
2(OA + OC) + 2(OB + OD) > AB + BC + CD + DA
2AC + 2BD > AB + BC + CD + DA
Therefore, AB + BC + CD + DA < 2(AC + BD)

6. The lengths of two sides of a triangle are 12 cm and 15 cm. Between what two measures should the length of the third side fall?

Given: Length of the two sides of the triangle are 12cm and 15cm
Let X cm be the length of the third side of the triangle.

In a triangle, the sum of the lengths of any two sides is greater than the third side.

i.e the third side has to be less than the sum of the two sides
12cm + 15cm > X cm
27cm > Xcm
X cm < 27cm

Also, the side cannot be less than the difference of the two sides
Xcm > 15cm – 12cm
Xcm > 3cm
3 cm < X < 27 cm

The length of the third side could be any length greater than 3 cm and less than 27 cm.

NCERT Solutions for Class 7 Maths Chapter 6 Exercise 6.5

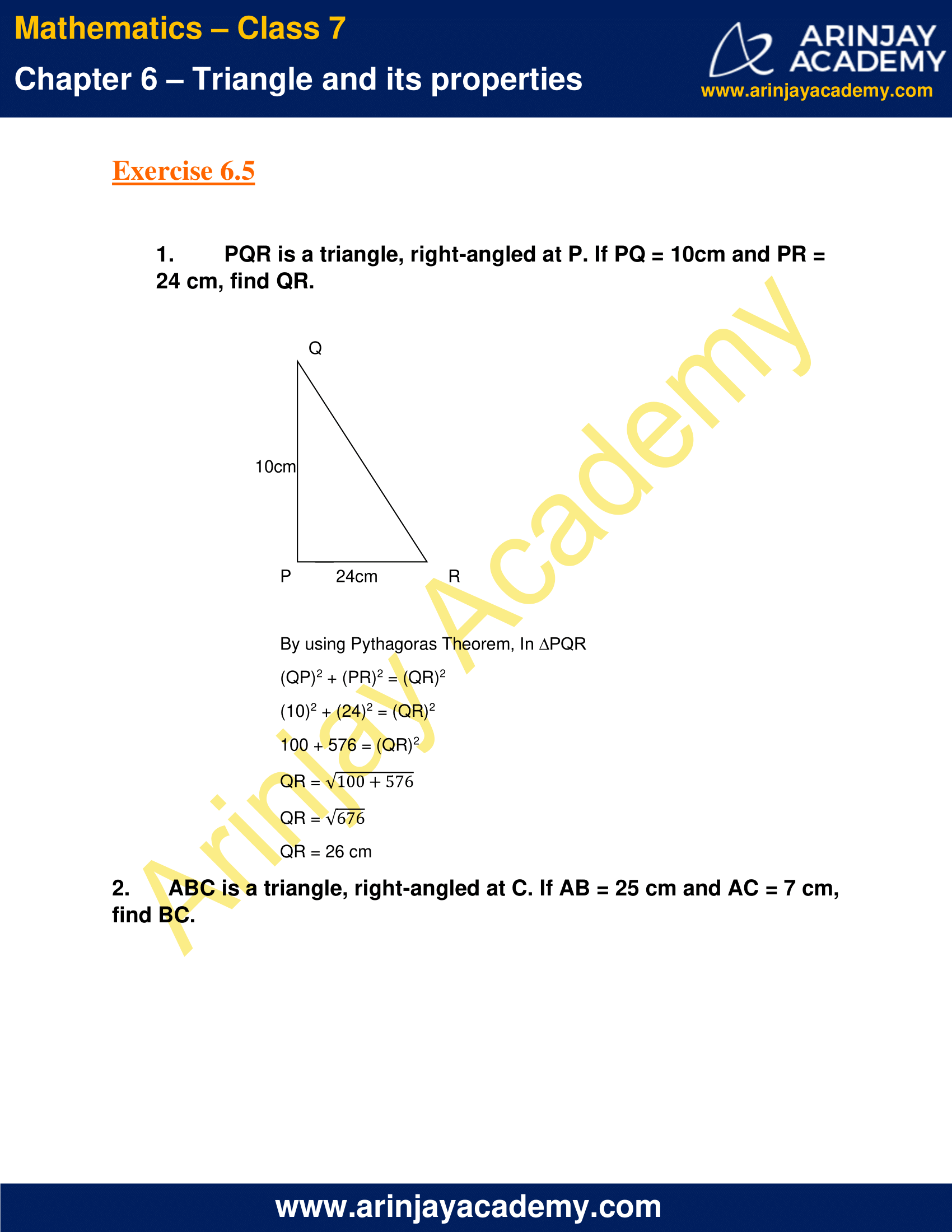
1. PQR is a triangle, right-angled at P. If PQ = 10cm and PR = 24 cm, find QR.

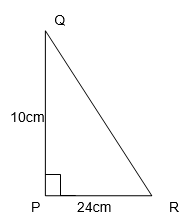
By using Pythagoras Theorem, In ∆PQR
(QP)² + (PR)² = (QR)²
(10)² + (24)² = (QR)²
100 + 576 = (QR)²
QR = √(100+576)
QR = √676
QR = 26 cm

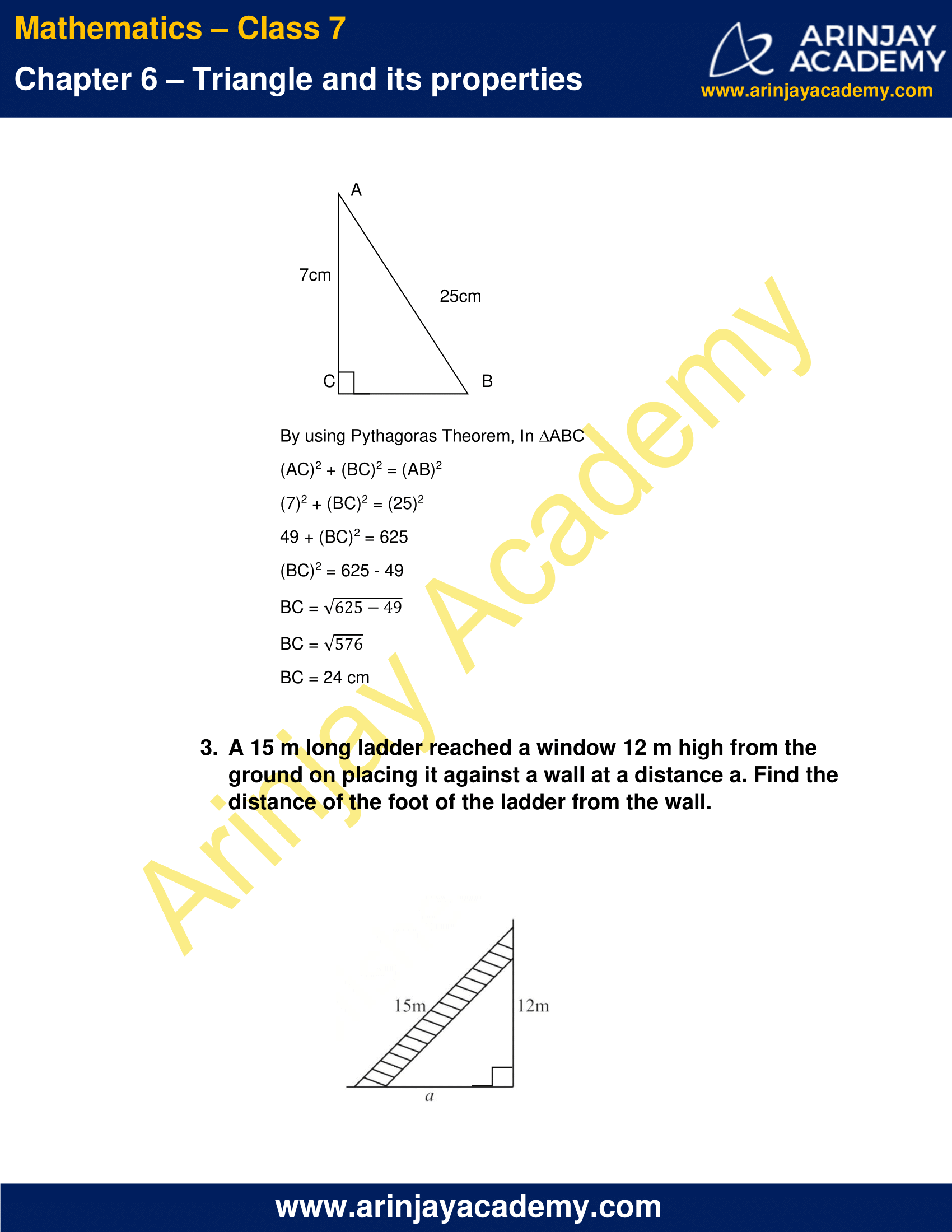
2. ABC is a triangle, right-angled at C. If AB = 25 cm and AC = 7 cm, find BC.

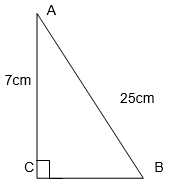
By using Pythagoras Theorem, In ∆ABC
(AC)² + (BC)² = (AB)²
(7)² + (BC)² = (25)²
49 + (BC)² = 625
(BC)² = 625 – 49
BC = √(625-49)
BC = √576
BC = 24 cm

3. A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance a. Find the distance of the foot of the ladder from the wall.

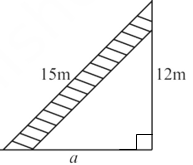
By using Pythagoras Theorem
a² + (12)²  = (15)²
a² = (15)² – (12)²
a² = 225 – 144
a² = 81
a = √81
a = 9 m
Hence, the distance of the foot of the ladder from the wall is 9 m.

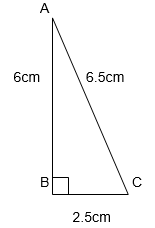
4. Which of the following can be the sides of a right triangle?

i) 2.5 cm,6.5 cm, 6 cm.
(2.5)² = 6.25
(6.5)² = 42.25
(6)² = 36

36 + 6.25 = 42.25
(6)² + (2.5)² = (6.5)²

Pythagoras Theorem holds true; therefore, these sides are of a right triangle.

(ii) 2 cm, 2 cm, 5 cm
(2)² = 4
(2)² = 4
(5)² = 25
(2)² + (2)² ≠ (5)²
Therefore, these sides are not of a right triangle.

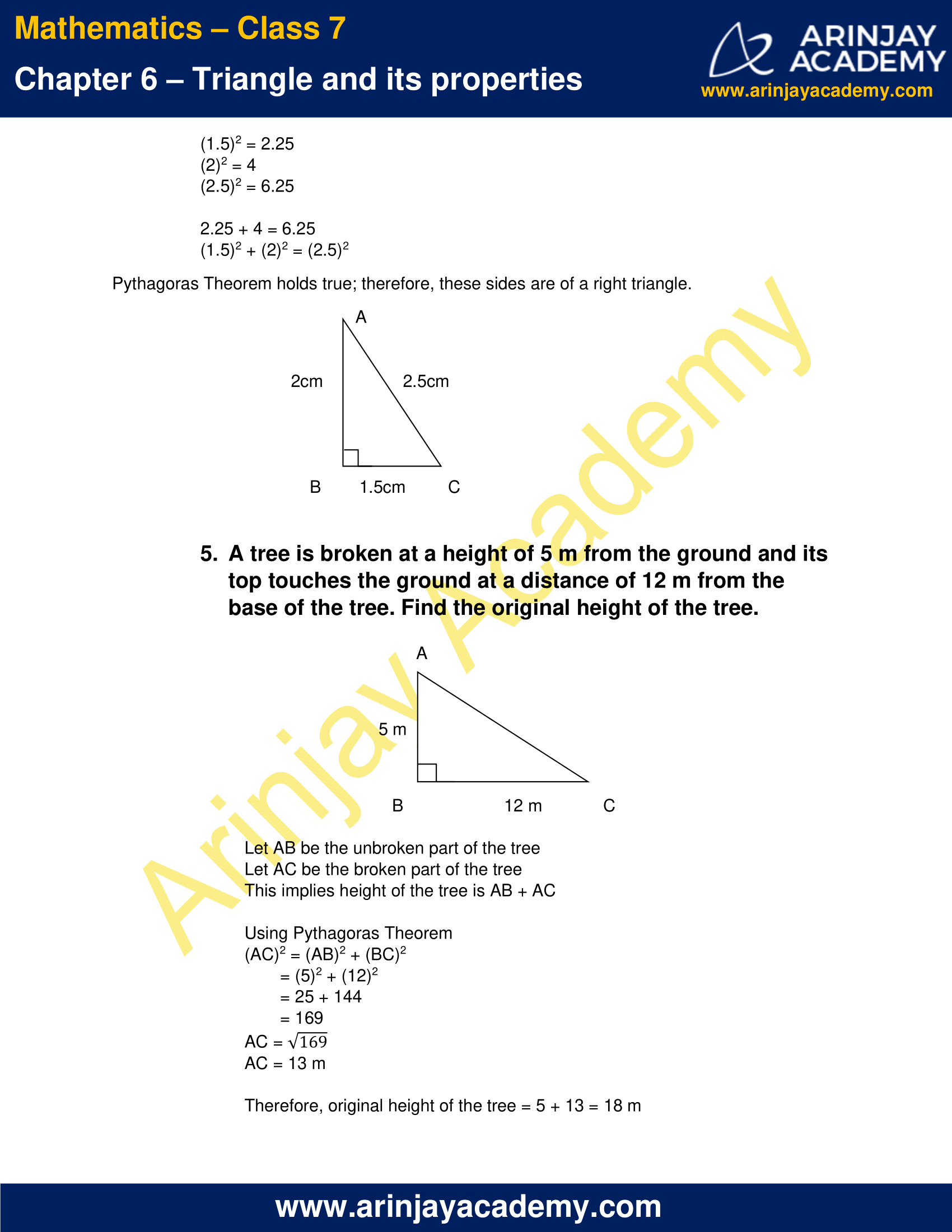
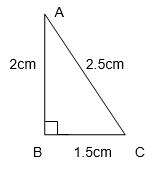
(iii) 1.5 cm, 2cm, 2.5 cm.
(1.5)² = 2.25
(2)² = 4
(2.5)² = 6.25

2.25 + 4 = 6.25
(1.5)² + (2)² = (2.5)²

Pythagoras Theorem holds true; therefore, these sides are of a right triangle.

5. A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.

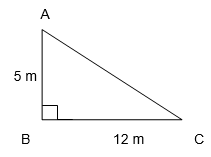
Let AB be the unbroken part of the tree
Let AC be the broken part of the tree
This implies height of the tree is AB + AC

Using Pythagoras Theorem
(AC)² = (AB)² + (BC)²
= (5)² + (12)²
= 25 + 144
= 169
AC = √169
AC = 13 m

Therefore, original height of the tree = 5 + 13 = 18 m

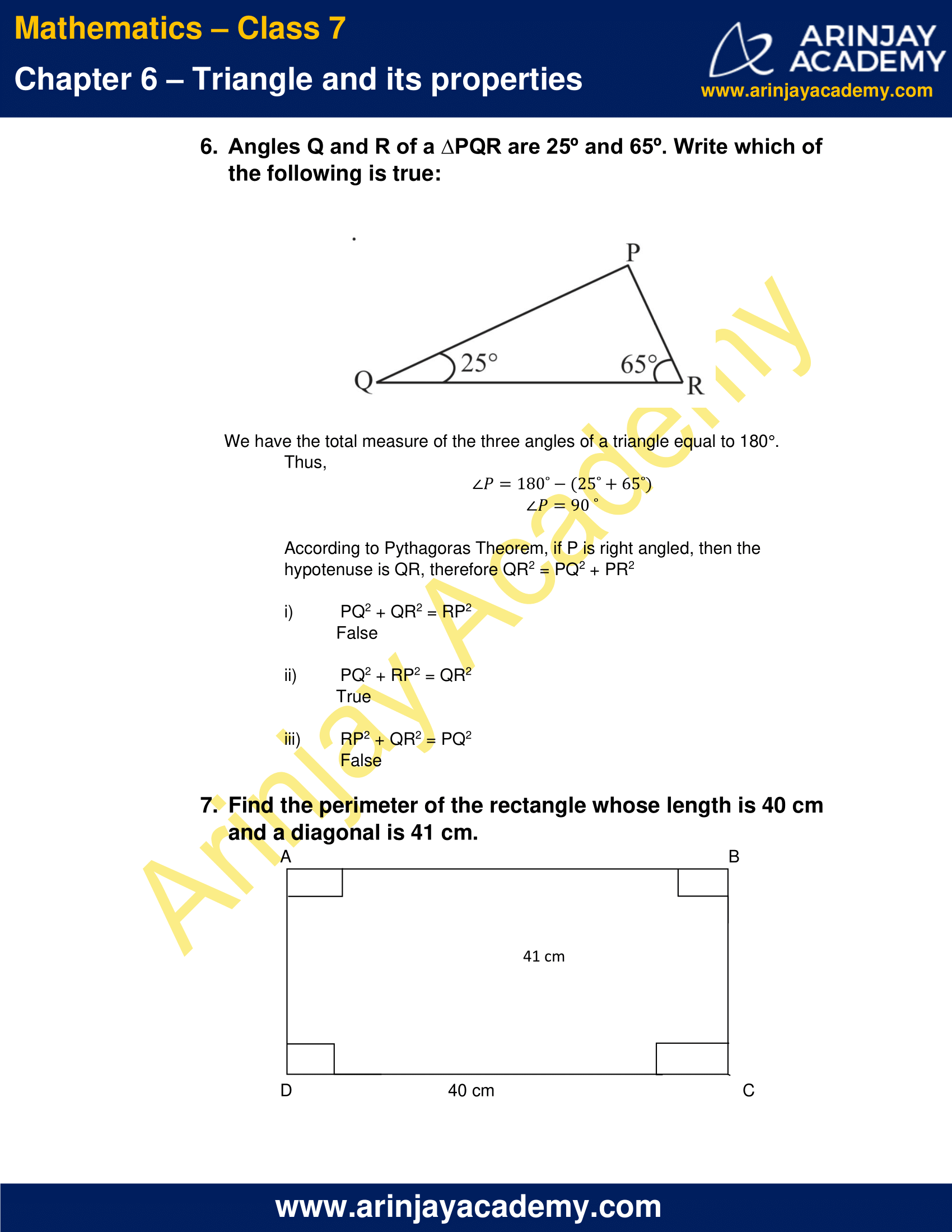
6. Angles Q and R of a ∆PQR are 25º and 65º. Write which of the following is true:

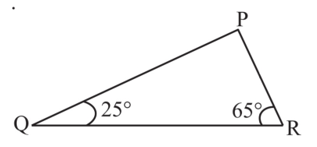
We have the total measure of the three angles of a triangle equal to 180°.
Thus,

∠P = 180^o – (25^o +65^o )
∠P = 90^o

According to Pythagoras Theorem, if P is right angled, then the hypotenuse is QR, therefore QR² = PQ² + PR²

(i) PQ² + QR² = RP²
False

(ii) PQ² + RP² = QR²
True

(iii) RP² + QR² = PQ²
False

7. Find the perimeter of the rectangle whose length is 40 cm and a diagonal is 41 cm.

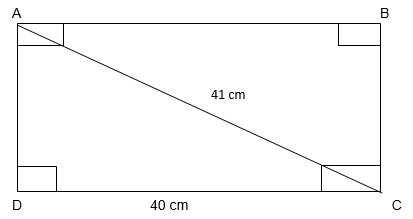
Since the edges of the rectangle form right angles
Using Pythagoras Theorem, In ∆ADC
(AD)² + (DC)² = (AC)²
(AD)² = (AC)² – (DC)²
= 41² – 40²
= 1681 – 1600
= 81
AD = √81
AD = 9 cm

Perimeter of Rectangle = 2 ( Length + Breadth)
= 2( DC + AD)
= 2(40 + 9)
=2(49)
Perimeter of Rectangle = 98 cm

8. The diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter.

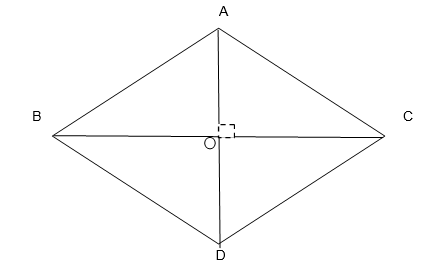
Let ABCD be a rhombus with all sides having equal length
Given AD = 16 cm
Therefore, AO = AD/2 = 16/2 = 8 cm
Given BC = 30 cm
Therefore, OC = BC/2 = 30/2 = 15 cm
The diagonals of a rhombus bisect each other at 90^o
Consider the right triangle ∆AOC
Using Pythagoras Theorem,
(AC)² = (AO)² + (OC)²
= 8² + 15²
= 64 + 225
= 289
AC = √289
AC = 17 cm
The length of the side of rhombus is 17 cm
Thus, the perimeter of rhombus = 4 x Side of the rhombus
Perimeter of Rhombus = 4 x 17 = 68 cm

With this we come to the end of NCERT Solutions for Class 7 Maths Chapter 6 Triangle and its properties. We hope these helped you study your subject.

• Maths NCERT Solutions Class 7
• NCERT Solutions Class 7

NCERT Solutions for Class 7 Maths Chapter 6 – Triangle and its properties