NCERT Solutions for Class 7 Maths Chapter 5 – Lines and Angles

Class 7 Maths NCERT Solutions Chapter 5 – Lines and Angles comprises of the 2 Exercises

• Exercise 5.1
• Exercise 5.2

This Chapter contains the Exercises relating to the following topics , which are discussed in Chapter 5 – Lines and Angles Class 7 NCERT book  : –

• 5.1 INTRODUCTION
• 5.2 RELATED ANGLES
• 5.2.1 Complementary Angles
• 5.2.2 Supplementary Angles
• 5.2.3. Adjacent Angles
• 5.2.4 Linear Pair
• 5.2.5 Vertically Opposite Angles
• 5.3 PAIRS OF LINES
• 5.3.1 Intersecting Lines
• 5.3.2 Transversal
• 5.3.3. Angles made by a Transversal
• 5.3.4 Transversal of Parallel Lines
• 5.4 CHECKING FOR PARALLEL LINES

NCERT Solutions for Class 7 Maths Chapter 5 – Exercise 5.1

NCERT Solutions for Class 7 Maths Chapter 5 – Exercise 5.2

NCERT Solutions for Class 7 Maths Chapter 5 – Exercise 5.1

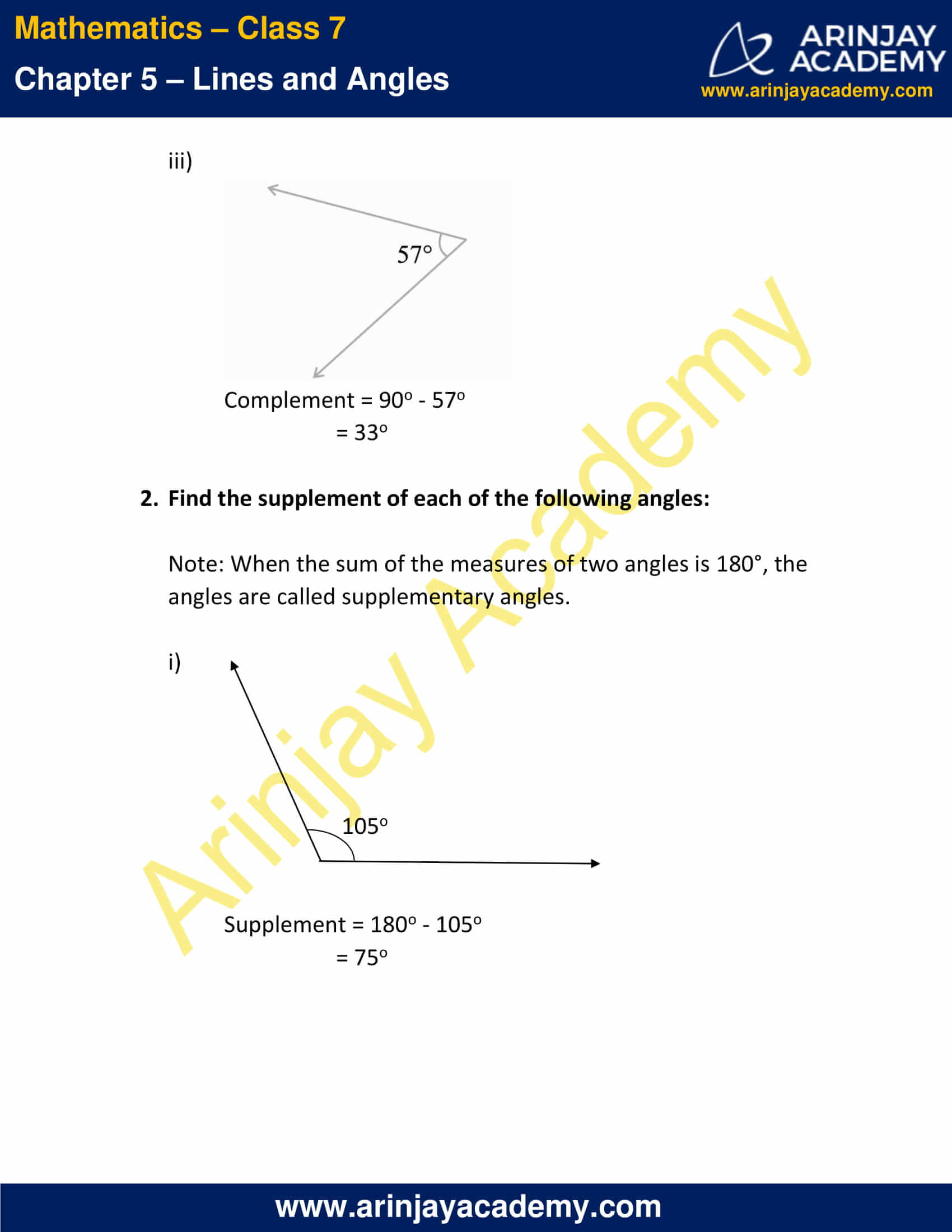
1. Find the complement of each of the following angles:

Note: When the sum of the measures of two angles is 90°, then the angles are called complementary angles.

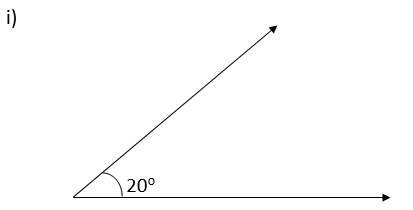
Complement = 90^o – 20^o
= 70^o

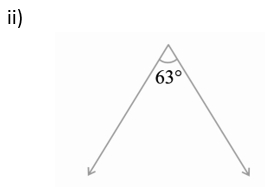
Complement = 90 ^o – 63 ^o
= 27 ^o

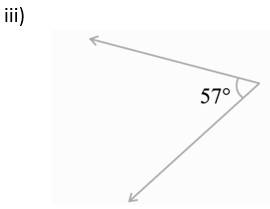
Complement = 90 ^o – 57 ^o
= 33 ^o

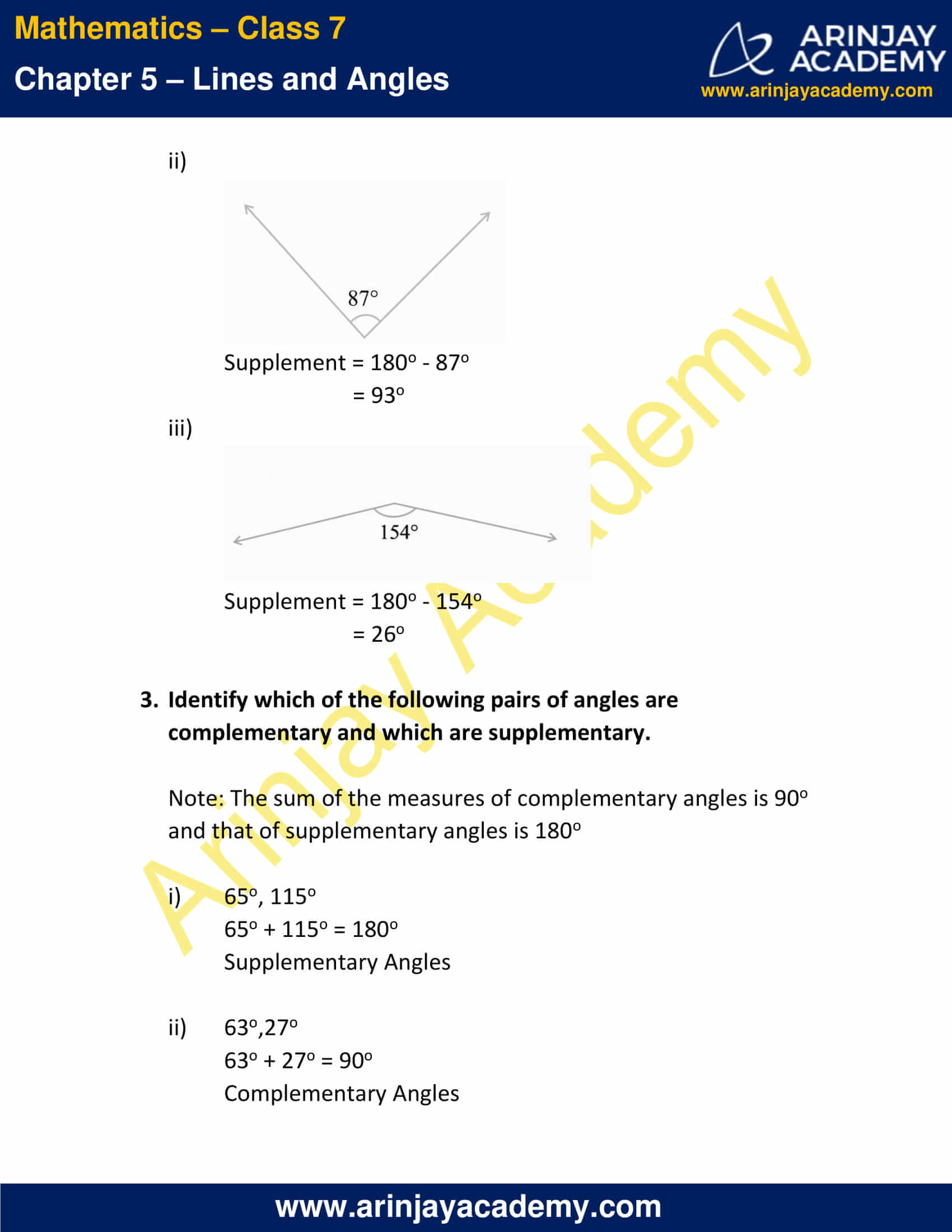
2. Find the supplement of each of the following angles:

 Note: When the sum of the measures of two angles is 180°, the angles are called supplementary angles.

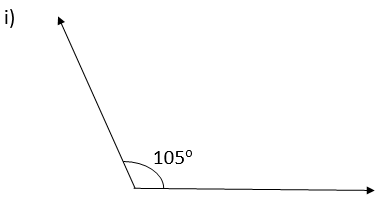
Supplement = 180 ^o – 105 ^o
= 75 ^o

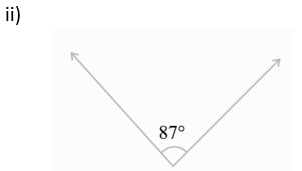
Supplement = 180 ^o – 87 ^o
= 93 ^o

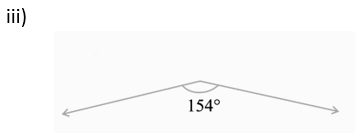
Supplement = 180 ^o – 154 ^o
= 26 ^o

3. Identify which of the following pairs of angles are complementary and which are supplementary.

Note: The sum of the measures of complementary angles is 90 ^o and that of supplementary angles is 180 ^o

i) 65 ^o, 115 ^o
65 ^o + 115 ^o = 180 ^o
Supplementary Angles

ii) 63 ^o,27 ^o
63 ^o + 27 ^o = 90^o
Complementary Angles

iii) 112 ^o, 68 ^o
112 ^o + 68 ^o = 180 ^o
Supplementary Angles

iv) 130 ^o,50 ^o
130 ^o + 50 ^o = 180 ^o
Supplementary Angles

v) 45 ^o, 45 ^o
45 ^o +45 ^o = 90 ^o
Complementary Angles

vi) 80 ^o,10 ^o
80 ^o + 10 ^o = 90 ^o
Complementary Angles

4. Find the angle which is equal to its complement.

Let the angle be X
Given the complement of X is X
We know that the sum of the measures of complementary angles is 90 ^o
Therefore, X ^o + X ^o = 90 ^o
2X ^o = 90 ^o
X ^o = 90/2
X  = 45 ^o
Thus, 45 ^o is equal to its complement.

5. Find the angle which is equal to its supplement. 

Let the angle be Y
Given the supplement of Y is Y
We know that the sum of the measures of supplementary angles is 180 ^o
Therefore, Y^o + Y ^o = 180^o
2Y ^o = 180^o
Y^o = 180/2
Y^o  = 90^o
Thus, 90 ^o is equal to its supplement.

6. In the given figure, ∠1 and ∠2 are supplementary angles. If ∠1 is decreased, what changes should take place in ∠2 so that both the angles still remain supplementary.

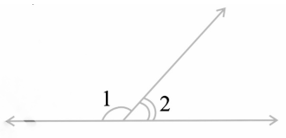
Given : ∠1 and ∠2 are supplementary angles i.e ∠1 + ∠2 = 180^o
If ∠1 is reduced by say x^o then ∠2 should be increased by x^o so that the angles still remain supplementary
i.e ∠1 – x^o + ∠2 + x^o = 180^o

7. Can two angles be supplementary if both of them are:

i) Acute?
No.
Acute angles are angles that are less than 90^o
Consider the sum of largest acute angle
89^o + 89^o = 178^o ≠ 180^o

ii) Obtuse?
No.
Obtuse angles are angles that are greater than 90^o and less than 180^o
Consider the sum of the smallest obtuse angle
91^o + 91^o = 182^o > 180^o

iii) Right?
Yes.
90^o + 90^o = 180^o
Therefore, two right angles are supplementary angles.

8. An angle is greater than 45^o. Is its complementary angle greater than 45^o or equal to 45^o or less than 45^o?

 Given an angle X > 45^o
And complement of X is 90^o – X

i.e X > 45^o implies -X < -45^o
Add 90^o on both sides
90^o – X < 90 – 45^o
90^o – X < 45^o
Clearly, the complementary angle of X is less than 45^o

9. In the adjoining figure:

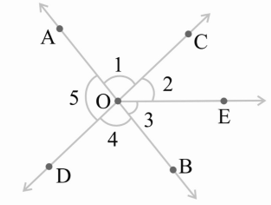
i) Is ∠1 adjacent to ∠2?
Yes, because:
Common vertex = O
Common arm = OC
AO and OE are on either side of OC

ii) Is ∠AOC adjacent to ∠AOE?
No,
∠AOC = ∠1 and ∠AOE = ∠1 + ∠2
Adjacent angles have no common interior points, here, both the angles have ∠1 as common interior point.

iii) Do ∠COE and ∠EOD form a linear pair?
Yes.
They form a linear pair because, the non-common arm arms OC and OD are opposite rays.

iv) Are ∠BOD and ∠DOA supplementary?
Yes.
∠BOD and ∠DOA are linear pairs and angles in linear pairs are supplementary.

v) Is ∠1 vertically opposite to ∠4?
Yes. AB and CD intersect at O, therefore ∠1 are ∠4 are vertically opposite angles.

vi) What is the vertically opposite angle of ∠5?
AB and CD intersect at O.
∠AOD is vertically opposite to ∠COB
i.e ∠5 is vertically opposite to ∠COB = ∠2 + ∠3

10. Indicate which pairs of angles are:

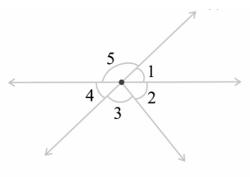
i) Vertically opposite angles.
∠1 and ∠4
∠5 and ∠2 + ∠3

ii) Linear pairs
∠5 and ∠1
∠4 and ∠5

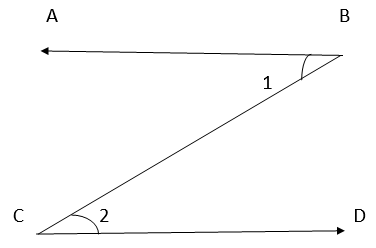
11. In the following figure, is ∠1 adjacent to ∠2? Give reasons.

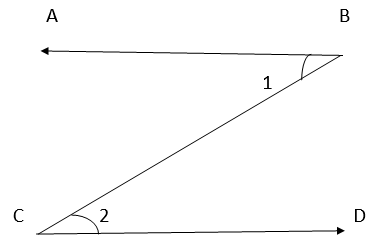
∠1 and ∠2 do not have a common vertex, hence they are not adjacent to each other.

12. Find the values of the angles x , y and z in each of the following:

i)

∠x = 55^o  (Vertically opposite angles are equal)
∠x and ∠y are supplementary since they are linear pairs, therefore, ∠x + ∠y = 180^o
∠y = 180^o – 55^o
∠y = 125^o

∠z = 125^o  (Vertically opposite angles are equal. Here ∠z and ∠y are vertically opposite to each other)

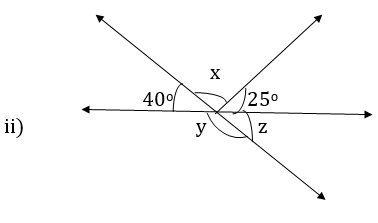
∠y + 40^o  = 180^o   [Linear pair of Angles]
y = 180^o – 40^o
y = 140^o
y and z form linear pair, implying that they are supplementary.
i.e y + z = 180^o
z = 180^o – y
= 180^o – 140^o
z = 40^o

Alternative Method: z = 40^o (Vertically opposite angles)
40^o + x + 25^o = 180^o    [Angles on Straight line]
x + 65^o = 180^o
x = 180^o – 65^o
x = 115^o

13. Fill in the blanks:

i) If two angles are complementary, then the sum of their measures is __________.
Ans: 90^o

ii) If two angles are supplementary, then the sum of their measures is __________.
Ans: 180^o

iii) Two angles forming a linear pair are ___________.
Ans: Supplementary

iv) If two adjacent angles are supplementary, they form a____________.
Ans: Linear pair.

v) If two lines intersect at a point, then the vertically opposite angles are always ___________.
Ans: Equal

vi) If two lines intersect at a point, and if one pair of vertically opposite angles are acute angles, then the other pair of vertically opposite angles are___________.
Ans: Obtuse angles

14. In the adjoining figure, name the following pairs of angles.

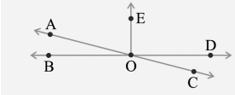
i) Obtuse vertically opposite angles
Ans: ∠AOD and ∠BOC

ii) Adjacent complementary angles
Ans: ∠EOA and ∠AOB

iii) Equal supplementary angles
Ans: ∠EOD and ∠EOB

iv) Unequal supplementary angles
Ans: ∠EOA and ∠EOC, ∠DOC and ∠COB

v) Adjacent angles that do not form a linear pair
Ans: ∠EOD and ∠DOC, ∠AOE and ∠EOD, ∠AOB and ∠EOA

NCERT Solutions for Class 7 Maths Chapter 5 – Exercise 5.2

1. State the property that is used in each of the following statements?

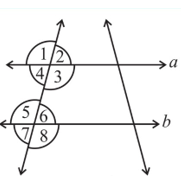
i) If a || b, then ∠1 = ∠5.
Corresponding Angles Property

ii) If ∠4 = ∠6, then a || b.
Alternate Interior Angles Property

iii) If ∠4 + ∠5 = 180°, then a || b.
When a transversal cuts two lines, such that pairs of interior angles on the same side of the transversal are supplementary.

2. In the adjoining figure, identify

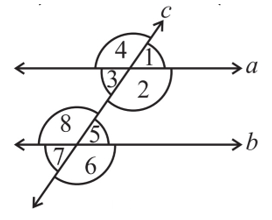
i) the pairs of corresponding angles.
∠4 and ∠8
∠1 and ∠5
∠3 and ∠7
∠2 and ∠6

ii) the pairs of alternate interior angles.
∠3 and ∠5
∠2 and ∠8

iii) the pairs of interior angles on the same side of the transversal.
∠3 and ∠8
∠2 and ∠5

iv) the vertically opposite angles
∠4 and ∠2
∠1 and ∠3
∠8 and ∠6
∠5 and ∠7

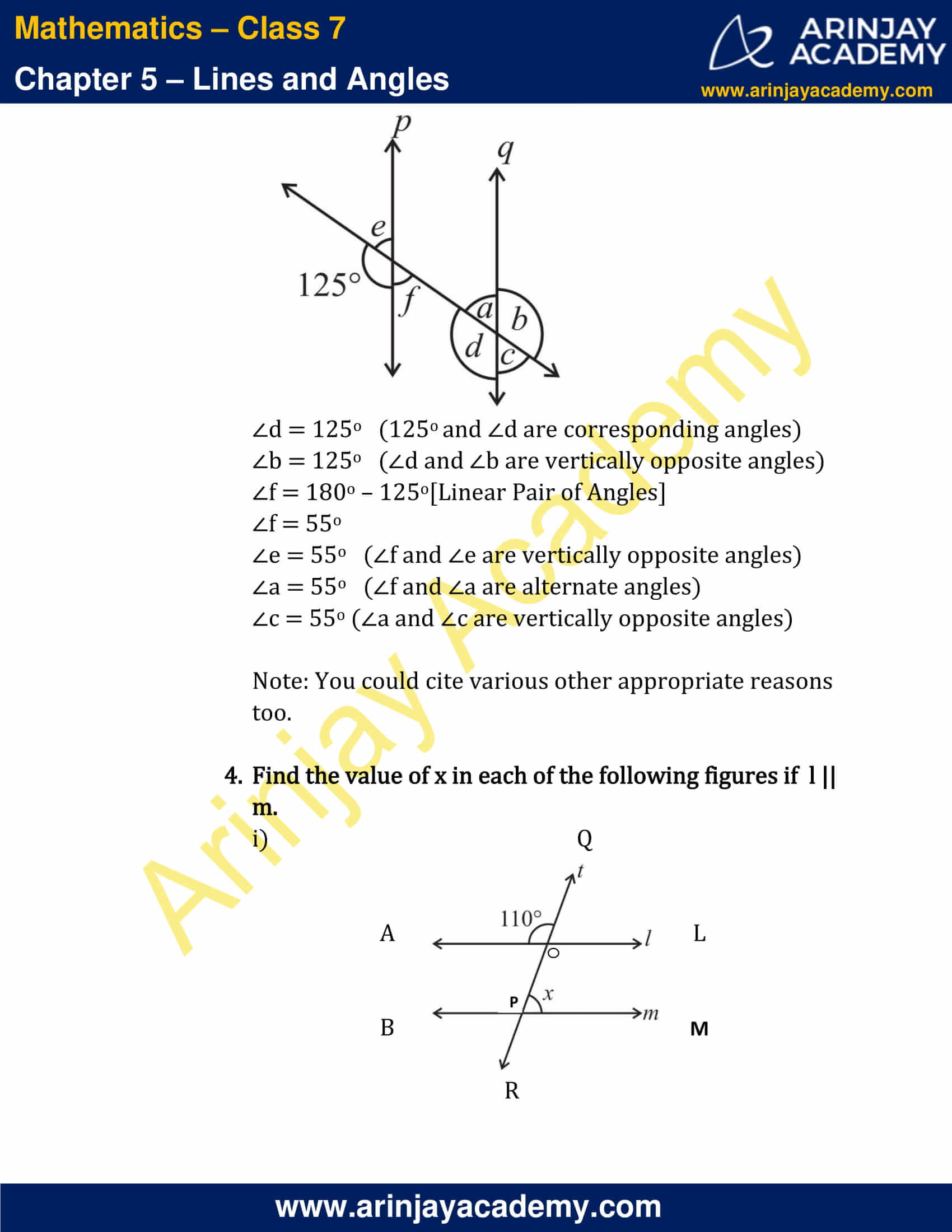
3. In the adjoining figure, p || q. Find the unknown angles.

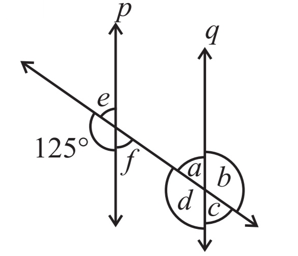
∠d = 125^o   (125^o and ∠d are corresponding angles)
∠b = 125^o   (∠d and ∠b are vertically opposite angles)
∠f = 180^o – 125^o [Linear Pair of Angles]
∠f = 55^o
∠e = 55^o   (∠f and ∠e are vertically opposite angles)
∠a = 55^o   (∠f and ∠a are alternate angles)
∠c = 55^o (∠a and ∠c are vertically opposite angles)

Note: You could cite various other appropriate reasons too.

4. Find the value of x in each of the following figures if l || m.

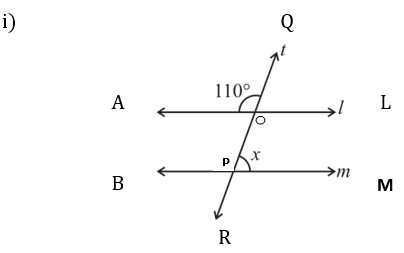
Given l||m
∠QOL = 180^o – 110^o [Linear pair of angles]
∠QOL = 70^o
x = 70^o [∠QOL and ∠OPM are Corresponding Angles]

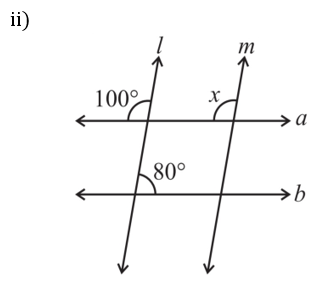
Given l || m
x = 100^o (Corresponding angles)

5. In the given figure, the arms of two angles are parallel. If ∠ABC = 70^o, then find

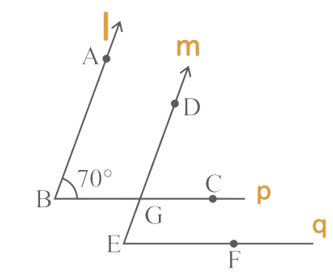
i) ∠DGC
Given l || m
∠DGC = ∠ABC = 70^o (Corresponding angles)

ii) ∠DEF
Given p || q
∠DEF = ∠DGC = 70^o   (Corresponding angles)

6. In the given figures below, decide whether l is parallel to m.

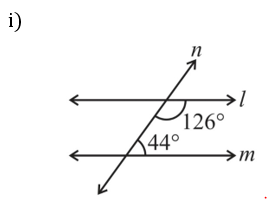
When a transversal cuts two lines, such that pairs of interior angles on the same side of the transversal are supplementary, the lines have to be parallel.

126^o + 44^o = 170^o ≠180^o

Therefore, l is not parallel to m.

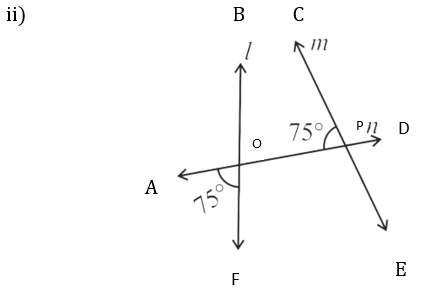
∠BOP = 75^o
When a transversal cuts two lines, such that pairs of interior angles on the same side of the transversal are supplementary, the lines have to be parallel.
Here, ∠BOP + ∠CPO = 75^o + 75^o
= 150^o ≠ 180^o
Therefore, l is not parallel to m.

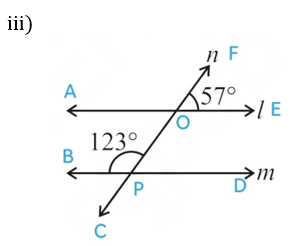
∠FOA = 180^o – 57^o = 123^o
∠FOA = ∠OPB = 123^o
When a transversal cuts two lines, such that pairs of corresponding angles are equal, then the lines have to be parallel.
Therefore, l is parallel to m

 

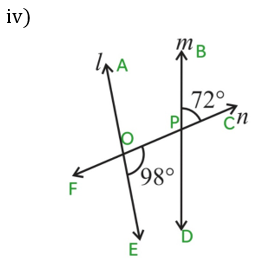
∠BPC = ∠OPD = 72^o  [Vertically Opposite Angles]
When a transversal cuts two lines, such that pairs of interior angles on the same side of the transversal are supplementary, the lines have to be parallel.
∠OPD + ∠POE = 72^o + 98^o
= 170^o ≠ 180^o
Therefore, l is not parallel to m

With this we come to the end of NCERT Solutions for Class 7 Maths Chapter 5 Lines and Angles. We hope these helped you study your subject.

• Maths NCERT Solutions Class 7
• NCERT Solutions Class 7

Download NCERT Solutions for Class 7 Maths Chapter 5 – Lines and Angles