Arinjay Academy » Maths Class 7 » NCERT Solutions for Class 7 Maths Chapter 4 – Simple Equations

NCERT Solutions for Class 7 Maths Chapter 4 – Simple Equations

Class 7 Maths NCERT Solutions Chapter 4 – Simple Equations comprises of the 4 Exercises,

Exercise 4.1
Exercise 4.2
Exercise 4.3
Exercise 4.4

NCERT Solutions for Class 7 Maths Chapter 4 Exercise 4.1

NCERT Solutions for Class 7 Maths Chapter 4 Exercise 4.2

NCERT Solutions for Class 7 Maths Chapter 4 Exercise 4.3

NCERT Solutions for Class 7 Maths Chapter 4 Exercise 4.4

NCERT Solutions for Class 7 Maths Chapter 4 Exercise 4.1

1. Complete the last column of the table:

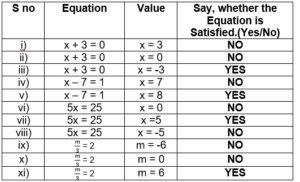
(i) No
Substitute x=3 in the equation x + 3 = 0
3 + 3 = 9 ≠ 0

(ii) No
Substitute x=0 in the equation x + 3 = 0
0 + 3 = 3 ≠ 0

(iii) Yes
Substitute x=-3 in the equation x + 3 = 0
-3+ 3 = 0

(iv) No
Substitute x=7 in the equation x – 7 = 1
7 – 7 = 0 ≠ 1

(v) Yes
Substitute x=8 in the equation x – 7 = 1
8- 7 = 1

(vi) No
Substitute x = 0 in the equation 5x = 25
5(0) = 0 ≠ 25

(vii) Yes
Substitute x = 5 in the equation 5x = 25
5(5) = 25

(viii) No
Substitute x = -5 in the equation 5x = 25
5(-5) = -25 ≠ 25

(ix) No
Substitute m = -6 in the equation $\cfrac { m }{ 3 }$ = 2
$\cfrac { -6 }{ 3 }$ = -2 ≠ 2

(x) No
Substitute m = 0 in the equation $\cfrac { m }{ 3 }$ = 2
$\cfrac { 0 }{ 3 }$ = 0 ≠ 2

(xi) Yes
Substitute m = 6 in the equation $\cfrac { m }{ 3 }$ = 2
$\cfrac { 6 }{ 3 }$ = 2

2. Check whether the value given in the brackets is a solution to the given equation or not:

a) n + 5 = 19 (n = 1)
1 + 5 = 6 ≠ 19
Therefore n = 1 is not a solution.

b) 7n + 5 = 19 (n = – 2)
7(-2) + 5 = -14 + 5
= -9 ≠ 19
Therefore n = -2 is not a solution.

c) 7n + 5 = 19 (n = 2)
7(2) + 5 = 14 + 5 = 19
Therefore n = 2 is a solution.

d) 4p – 3 = 13 (p = 1)
4(1) – 3 = 4 – 3 = 1 ≠ 13
Therefore p = 1 is not a solution

e) 4p – 3 = 13 (p = – 4)
4(-4) – 3 = -16 – 3
= -19 ≠ 13
Therefore p = -4 is not a solution

f) 4p – 3 = 13 (p = 0)
4(0) – 3 = 0 – 3
= -3 ≠ 13
Therefore p = 0 is not a solution

3. Solve the following equations by trial and error method

i) 5p + 2 = 17

p = 0
5(0) + 2 = 0 + 2
= 2 ≠ 17

p = 1
5(1) + 2 = 5 + 2
= 7 ≠ 17

p = -1
5(-1) + 2 = -5 + 2
= -3 ≠ 17

p = 2
5(2) + 2 = 10 + 2
= 12 ≠ 17

p = -2
5(-2) + 2 = -10 +2
= -8 ≠ 17

p = 3
5(3) + 2 = 15 + 2
= 17

Therefore p=3 is a solution of the equation.

ii) 3m – 14 = 4

m = 0
3(0) – 14 = 0 – 14
= -14 ≠ 4

m = 1
3(1) – 14 = 3 – 14
= -11 ≠ 4

m = -1
3(-1) – 14 = -3 -14
= – 17

m = 2
3(2) – 14 = 6 – 14
= -8 ≠ 4

.
.
.
.

m = 6
3(6) – 14 = 18 – 14
= 4

Therefore m = 6 is a solution of the equation

4. Write equations for the following statements

(i) The sum of numbers x and 4 is 9.
Sum of x and 4 is x + 4
The sum is 9
Therefore the equation is x + 4 = 9

(ii) 2 subtracted from y is 8.
2 subtracted from is y – 2
The given difference is 8
Therefore the equation is y – 2 = 8

(iii) Ten times a is 70
Ten times a is 10 x a i.e 10a
The given product is 70
Therefore the equation is 10a = 70

(iv) The number b divided by 5 gives 6.
Number b divided by 5 is $\cfrac { b }{ 5 }$
The division gives quotient 6
Therefore the equation $\cfrac { b }{ 5 }$ is = 6

(v) Three-fourth of t is 15.
Three-fourth of t is $\cfrac { 3 }{ 4 }$ t
Therefore the equation is $\cfrac { 3 }{ 4 }$ t = 15

(vi) Seven times m plus 7 gets you 77
Seven times m is 7 x m i.e 7m
Seven times m plus 7 is 7m + 7
The sum yields 77
Therefore the equation is 7m + 7 = 77

(vii) One-fourth of a number x minus 4 gives 4.
One-fourth of a number x is $\cfrac { 1x }{ 4 }$
One-fourth of a number x minus 4 is $\cfrac { 1x }{ 4 }$ – 4
The difference yields 4
Therefore the equation is $\cfrac { 1x }{ 4 }$ – 4 = 4

(viii) If you take away 6 from 6 times y, you get 60.
6 times y is 6 x y i.e 6y
Taking away 6 from 6 times y is 6y – 6
The difference gives 60
Therefore the equation is 6y – 6 = 60

(ix) If you add 3 to one-third of z, you get 30.
One-third of z is $\cfrac { 1 }{ 3 }$ z
Add 3 to one-third of z is $\cfrac { 1 }{ 3 }$ z + 3
The sum gives 30
Therefore the equation is $\cfrac { 1 }{ 3 }$ z + 3 = 30

5. Write the following equations in statement forms:

i) p + 4 = 15
The sum of numbers p and 4 is 15

ii) m – 7 = 3
7 subtracted from m is 3

iii) 2m = 7
Two times m is 7

iv) $\cfrac { m }{ 5 }$ = 3
The number m divided by 5 gives 3

v) $\cfrac { 3m }{ 5 }$ = 6
Three times a number m divided by 5 gives 6

vi) 3p + 4 = 25
Three times p plus 4 gets 25

vii) 4p – 2 = 18
If you take 2 away from 4 times p, you get 18

viii) $\cfrac { p }{ 2 }$ + 2 = 8
If you add 2 to half of a number p you get 8

6. Set up an equation in the following cases:

i) Irfan says that he has 7 marbles more than five times the marbles Parmit has. Irfan has 37 marbles. (Take m to be the number of Parmit’s marbles.)

Solution:

Number of marbles Parmit has = m
Five times Parmit marbels = 5m
Irfan has 7 marbles more than five times the marbles Parmit has i.e 5m + 7
Number of marbles Irfan has = 37
Therefore, the equation is 5m + 7 = 37

ii) Laxmi’s father is 49 years old. He is 4 years older than three times Laxmi’s age. (Take Laxmi’s age to be y years.)

Solution:

Laxmi’s age = y years
Three times Laxmi’s age = 3y
Laxmi’s father is 4 years older than three times Laxmi’s age i.e 3y + 4
Laxmi’s father’s age = 49 years
Therefore, the equation is 3y + 4 = 49

iii) The teacher tells the class that the highest marks obtained by a student in her class is twice the lowest marks plus 7. The highest score is 87. (Take the lowest score to be l.)

Solution:

Lowest score = l
Twice the lowest marks = 2l
The highest marks obtained by a student in class is twice the lowest marks plus 7 i.e 2l + 7
The highest score = 87
Therefore the equation is 2l +7 = 873

iv) In an isosceles triangle, the vertex angle is twice either base angle. (Let the base angle be b in degrees. Remember that the sum of angles of a triangle is 180 degrees).

Solution:

Let the angles of the Isosceles triangle be b^o, b^o and v^oWhere b^o is the base angles and v^o is the vertex angle
The vertex angle is twice either base angle i.e v^o = 2b^oSum of angles of a triangle = 180^oi.e b^o + b^o + v^o = 180^oi.e b^o + b^o+ 2b^o = 180^o (by substituting the value of v^o)
Therefore the equation is 3b^o= 180

NCERT Solutions for Class 7 Maths Chapter 4 Exercise 4.2

1. Give first the step you will use to separate the variable and then solve the equation.

a) x – 1 = 0
Add 1 to both sides of the equation
x – 1 + 1 = 0 + 1
Hence x = 1

b) x + 1 = 0
Subtract 1 from both sides of the equation
x + 1 – 1 = 0 – 1
Hence x = -1

c) x – 1 = 5
Add 1 to both sides of the equation
x – 1 + 1 = 5 + 1
Hence x = 6

d) x + 6 = 2
Subtract 6 from both sides of the equation
x + 6 – 6 = 2 – 6
Hence x = -4

e) y – 4 = -7
Add 4 to both sides of the equation
y – 4 + 4 = -7 + 4
Hence y = -3

f) y – 4 = 4
Add 4 to both sides of the equation
y – 4 +4 = 4 + 4
Hence y = 8

g) y + 4 = 4
Subtract 4 from both sides of the equation
y + 4 – 4 = 4 – 4
Hence y = 0

h) y + 4 = – 4
Subtract 4 from both sides of the equation
y + 4 – 4 = -4 – 4
Hence y = -8

2. Give first the step you will use to separate the variable and then solve the equation:

a) 3l = 42
Dividing both sides by 3 we get,
$\cfrac { 3l }{ 3 }$ = $\cfrac { 42 }{ 3 }$
Hence l = 14

b) $\cfrac { b }{ 2 }$ = 6
Multiplying both sides by 2 we get,
$\cfrac { b }{ 2 }$ (2) = 6(2).
Hence b = 12

c) $\cfrac { p }{ 7 }$ = 4
Multiplying both sides by 7 we get,
$\cfrac { p }{ 7 }$ (7) = 4 (7)
Hence p = 28

d) 4x = 25
Dividing both sides by 4 we get,
$\cfrac { 4x }{ 4 }$ = $\cfrac { 25 }{ 4 }$
Hence x = $\cfrac { 25 }{ 4 }$

e) 8y = 36
Dividing both sides by 8 we get,
$\cfrac { 8y }{ 8 }$ = $\cfrac { 36 }{ 8 }$
Hence y = $\cfrac { 36 }{ 8 }$ = $\cfrac { 9 }{ 2 }$

f) $\cfrac { z }{ 3 }$ = $\cfrac { 5 }{ 4 }$
Multiplying both sides by 3 we get,
$\cfrac { z }{ 3 }$ x (3) = $\cfrac { 5 }{ 4 }$ x (3)
Hence z = $\cfrac { 15 }{ 4 }$

g) $\cfrac { a }{ 5 }$ = $\cfrac { 7 }{ 15 }$
Multiplying both sides by 5 we get,
$\cfrac { a }{ 5 }$ x (5) = $\cfrac { 7 }{ 15 }$ x (5)
Hence a = $\cfrac { 7 }{ 3 }$

h) 20t = -10
Dividing both sides by 20 we get,
$\cfrac { 20t }{ 20 }$ = $\cfrac { -10 }{ 20 }$
Hence t = $\cfrac { -1 }{ 2 }$

3. Give the steps you will use to separate the variable and then solve the equation

a) 3n – 2 = 46
Adding 2 to both sides we get,
3n – 2 + 2 = 46 + 2
3n = 48
Dividing both sides by 3 we get,
$\cfrac { 3n }{ 3 }$ = $\cfrac { 48 }{ 3 }$
Hence n = 16

b) 5m + 7 = 17
Subtracting 7 from both sides we get,
5m + 7 – 7 = 17 – 7
5m = 10
Dividing both sides by 5 we get,
$\cfrac { 5m }{ 5 }$ = $\cfrac { 10 }{ 5 }$
Hence m = 2

c) $\cfrac { 20p }{ 3 }$ = 40
Multiplying both sides by 3 we get,
$\cfrac { 20p }{ 3 }$ (3) = 40(3)
20p = 40 (3)
Dividing both sides by 20 we get,
$\cfrac { 20p }{ 20 }$ = $\cfrac { 40(3) }{ 20 }$
Hence p = 6

d) $\cfrac { 3p }{ 10 }$ = 6
Multiplying both sides by 10 we get,
$\cfrac { 3p }{ 10 }$ (10) = 6(10)
3p = 60
Dividing both sides by 3 we get,
$\cfrac { 3p }{ 3 }$ = $\cfrac { 60 }{ 3 }$
Hence p = 20

4. Solve the following equations:

(a) 10p = 100
Dividing both sides by 10 we get,
$\cfrac { 10p }{ 10 }$ = $\cfrac { 100 }{ 10 }$
Hence p = 10

(b) 10p + 10 = 10
Subtracting 10 from both sides we get,
10p + 10 – 10 = 10 – 10
10p = 0
Dividing both sides by 10 we get,
$\cfrac { 10p }{ 10 }$ = $\cfrac { 0 }{ 10 }$
Hence p = 0

(d) $\cfrac { -p }{ 3 }$ = 5
Multiplying both sides by -3 (so that p becomes positive)we get,
$\cfrac { -p }{ 3 }$ (-3) = 5(-3)
Hence p = -15

(e) $\cfrac { 3p }{ 4 }$ = 6
Multiplying both sides by 4 we get,
$\cfrac { 3p }{ 4 }$ (4) = 6(4)
3p = 24
Dividing both sides by 3 we get,
$\cfrac { 3p }{ 3 }$ = $\cfrac { 24 }{ 3 }$
Hence p = 8

(f) 3s = -9
Dividing both sides by 3 we get,
$\cfrac { 3s }{ 3 }$ = $\cfrac { -9 }{ 3 }$
Hence s = -3

(g) 3s + 12 = 0
Subtracting 12 from both sides we get,
3s + 12 – 12 = 0 – 12
3s = -12
Dividing both sides by 3 we get,
$\cfrac { 3s }{ 3 }$ = $\cfrac { -12 }{ 3 }$
Hence s = -4

(h) 3s = 0
Dividing both sides by 3 we get,
$\cfrac { 3s }{ 3 }$ = $\cfrac { 0 }{ 3 }$
Hence s = 0

(i) 2q = 6
Dividing both sides by 2 we get,
$\cfrac { 2q }{ 2 }$ = $\cfrac { 6 }{ 2 }$
Hence q = 3

(j) 2q – 6 = 0
Adding 6 to both sides we get,
2q -6 + 6 = 0 + 6
2q = 6
Dividing both sides by 2 we get,
$\cfrac { 2q }{ 2 }$ = $\cfrac { 6 }{ 2 }$
Hence q = 3

(k) 2q + 6 = 0
Subtracting 6 from both sides we get,
2q + 6 – 6 = 0 – 6
2q = -6
Dividing both sides by 2 we get,
$\cfrac { 2q }{ 2 }$ = $\cfrac { -6 }{ 2 }$
Hence q = -3

(l) 2q + 6 = 12
Subtracting 6 from both sides we get,
2q +6 – 6 = 12 – 6
2q = 6
Dividing both sides by 2 we get,
$\cfrac { 2q }{ 2 }$ = $\cfrac { 6 }{ 2 }$
Hence q = 3

NCERT Solutions for Class 7 Maths Chapter 4 Exercise 4.3

1. Solve the following equations

a) 2y + $\cfrac { 5 }{ 2 }$ = $\cfrac { 37 }{ 2 }$
Transposing (+ $\cfrac { 5 }{ 2 }$ ) to RHS we get,
2y = $\cfrac { 37 }{ 2 }$ – $\cfrac { 5 }{ 2 }$
2y = $\cfrac { 32 }{ 2 }$ = 16
Divide both sides by 2
$\cfrac { 2y }{ 2 }$ = $\cfrac { 16 }{ 2 }$
Hence y = 8

b)5t + 28 = 10
Transposing (+ 28) to RHS we get,
5t = 10 – 28
5t = -18
Divide both sides by 5
$\cfrac { 5t }{ 5 }$ = $\cfrac { -18 }{ 5 }$
Hence t = $\cfrac { -18 }{ 5 }$

c) $\cfrac { a }{ 5 }$ + 3 = 2
Transposing (+3) to RHS we get,
$\cfrac { a }{ 5 }$ = 2 – 3
$\cfrac { a }{ 5 }$ = -1
Multiplying both sides by 5
$\cfrac { a }{ 5 }$ (5) = -1 (5)
Hence a = -5

d) $\cfrac { q }{ 4 }$ + 7 = 5
Transposing (+7) to RHS we get,
$\cfrac { q }{ 4 }$ = 5 – 7
$\cfrac { q }{ 4 }$ = – 2
Multiply both sides by 4
$\cfrac { q }{ 4 }$ (4) = – 2(4)
Hence q = -8

e) $\cfrac { 5 }{ 2 }$ x = -5
Multiply both sides by 2
$\cfrac { 5x }{ 2 }$ (2) = -5(2)
5x = -10
Divide both sides by 5
$\cfrac { 5x }{ 5 }$ = $\cfrac { -10 }{ 5 }$
Hence x = -2

f) $\cfrac { 5x }{ 2 }$ = $\cfrac { 25 }{ 4 }$
Multiply both sides by 2
$\cfrac { 5x }{ 2 }$ (2) = $\cfrac { 25 }{ 4 }$ (2)
5x = = $\cfrac { 25 }{ 2 }$
Divide both sides by 5
= $\cfrac { 5x }{ 5 }$ = $\cfrac { 25 }{ 2 }$ . $\cfrac { 1 }{ 5 }$
Hence x = $\cfrac { 5 }{ 2 }$

g) 7m + $\cfrac { 19 }{ 2 }$ = 13
Transposing $\cfrac { +19 }{ 2 }$ to RHS we get,
7m = 13 – $\cfrac { 19 }{ 2 }$
7m = $\cfrac { 26 }{ 2 }$ – $\cfrac { 19 }{ 2 }$
7m = $\cfrac { 7 }{ 2 }$
Divide both sides by 7
7m = $\cfrac { 7 }{ 2 }$ . $\cfrac { 1 }{ 7 }$
Hence m = $\cfrac { 1 }{ 2 }$

h) 6z + 10 = -2
Transposing (+10) to RHS we get,
6z = -2 -10
6z = -12
Divide both sides by 6
$\cfrac { 6z }{ 6 }$ = $\cfrac { -12 }{ 6 }$
Hence z = -2

i) $\cfrac { 3l }{ 2 }$ = $\cfrac { 2 }{ 3 }$
Multiply both sides by $\cfrac { 2 }{ 3 }$
$\cfrac { 3l }{ 2 }$ . $\cfrac { 2 }{ 3 }$ = $\cfrac { 2 }{ 3 }$ . $\cfrac { 2 }{ 3 }$
Hence l = $\cfrac { 4 }{ 9 }$

j) $\cfrac { 2b }{ 3 }$ – 5 = 3
Transposing (-5) to RHS we get,
$\cfrac { 2b }{ 3 }$ = 3 + 5
$\cfrac { 2b }{ 3 }$ = 8
Multiply both sides by $\cfrac { 3 }{ 2 }$
$\cfrac { 2b }{ 3 }$ . $\cfrac { 3 }{ 2 }$ = 8. $\cfrac { 3 }{ 2 }$
Hence b = 12

2. Solve the following equations:

a) 2(x + 4) = 12
Divide both sides by 2, so as to remove the brackets in the LHS,we get,
x + 4 = $\cfrac { 12 }{ 2 }$
x + 4 = 6
Transposing (+4) to RHS we get,
x = 6 – 4
x = 2

b) 3(n – 5) = 21
Divide both sides by 3, so as to remove the brackets in the LHS,we get,
n – 5 = $\cfrac { 21 }{ 3 }$
n – 5 = 7
Transposing (-5) to RHS
n = 7 + 5
Hence n = 12

c) 3(n – 5) = – 21
Divide both sides by 3, so as to remove the brackets in the LHS,we get,
n – 5 = $\cfrac { -21 }{ 3 }$
n – 5 = -7
Transposing (-5) to RHS
n = -7 + 5
Hence n = -2

d) – 4(2 + x) = 8
Divide both sides by -4, so as to remove the brackets in the LHS,we get,
2 + x = $\cfrac { 8 }{ -4 }$
2 + x = -2
Transposing (+2) to RHS|
x = -2 – 2
Hence x = -4

e) 4(2 – x) = 8
Divide both sides by 4, so as to remove the brackets in the LHS,we get,
2 – x = $\cfrac { 8 }{ 4 }$
2 – x = 2
Transposing (+2) to RHS
-x = 2 – 2
-x = 0
Multiplying -1 (to make x positive) to both sides we get,
Hence x = 0

3. Solve the following equations:

a) 4 = 5(p – 2)
The above equation can also be written as 5(p – 2) = 4
Thus, divide both sides by 5, so as to remove the brackets in the LHS,we get,
p – 2 = $\cfrac { 4 }{ 5 }$
Transposing (-2) to RHS we get,
p = $\cfrac { 4 }{ 5 }$ + 2
p = $\cfrac { 4 }{ 5 }$ + $\cfrac { 10 }{ 5 }$
Hence p = $\cfrac { 14 }{ 5 }$

b) – 4 = 5(p – 2)
The above equation can also be written as 5(p – 2) = -4
Thus, divide both sides by 5, so as to remove the brackets in the LHS,we get,
p – 2 = $\cfrac { -4 }{ 5 }$
Transposing (-2) to RHS we get,
p = $\cfrac { -4 }{ 5 }$ + 2
p = $\cfrac { -4 }{ 5 }$ + $\cfrac { 10 }{ 5 }$
Hence p = $\cfrac { 6 }{ 5 }$

c) 16 = 4 + 3(t + 2)
The above equation can also be written as 4 + 3(t + 2) = 16
Transposing (+4) to RHS
3(t + 2) = 16 – 4
3(t + 2) = 12
Divide both sides by 3, so as to remove the brackets in the LHS,we get,
t + 2 = $\cfrac { 12 }{ 3 }$
t + 2 = 4
Transposing (+2) to RHS we get,
t = 4 – 2
Hence t = 2

d) 4 + 5(p – 1) =34
Transposing (+4) to RHS
5(p – 1) = 34 – 4
5(p – 1) = 30
Divide both sides by 5, so as to remove the brackets in the LHS,we get,
p – 1 = $\cfrac { 30 }{ 5 }$
p – 1 = 6
Transposing (-1) to RHS we get,
p = 6 + 1
Hence p = 7

e) 0 = 16 + 4(m – 6)
The above equation can also be written as 16 + 4(m – 6) = 0
Transposing (+16) to RHS
4(m – 6) = -16
Divide both sides by 4, so as to remove the brackets in the LHS,we get,
m – 6 = $\cfrac {-16 }{ 4 }$
m – 6 = -4
Transposing (-6) to RHS we get,
m = -4 + 6
Hence m = 2

4. a) Construct 3 equations starting with x = 2

(i) x = 2
Multiply both sides by 4
4x = 8

(ii) x = 2
Add 3 to both sides
x + 3 = 5

(iii) x = 2
Subtract 11 from both sides
x – 11 = 2 – 11
x – 11 = -9

b) Construct 3 equations starting with x = – 2

Follow the same steps as the previous question and construct 3 different equations.

You can multiply, divide, add or subtract any number as you wish.

NCERT Solutions for Class 7 Maths Chapter 4 Exercise 4.4

1. Set up equations and solve them to find the unknown numbers in the following cases:

a) Add 4 to eight times a number; you get 60

Let, the number be ‘x’
Eight times a number is 8x
Add 4 to eight times a number is 8x + 4
You get 60
i.e 8x + 4 = 60
8x = 60 – 4 (Transposing +4 to RHS)
8x = 56
Therefore x = 7 (Dividing both sides by 8)

b) One-fifth of a number minus 4 gives 3.
Let, the number be ‘x’
One-fifth of a number is $\cfrac { 1x }{ 5 }$
Subtracting 4 from it i.e $\cfrac { 1x }{ 5 }$ – 4
The result gives 3
i.e $\cfrac { 1x }{ 5 }$ – 4 = 3
$\cfrac { x }{ 5 }$ – $\cfrac { 20 }{ 5 }$ = 3
$\cfrac { x-20 }{ 5 }$ = 3 (Taking LCM)
x – 20 = 15 (Multiplying both sides by 5)
x = 15 + 20 (Transposing -20 to RHS)
Therefore x = 35

c) If I take three-fourths of a number and add 3 to it, I get 21.

Let, the number be ‘x’
Three-fourths of a number is $\cfrac { 3x }{ 4 }$
Add 3 to it $\cfrac { 3x }{ 4 }$ + 3
The result gives 21
i.e $\cfrac { 3x }{ 4 }$ + 3 = 21
$\cfrac { 3x }{ 4 }$ + $\cfrac { 12 }{ 4 }$ = 21 (Taking LCM)
$\cfrac { 3x+12 }{ 4 }$ = 21
3x + 12 = 84 (Multiplying both sides by 4)
3x = 84 – 12 (Transposing +12 to RHS)
3x = 72
Therefore x = 24 (Dividing both sides by 3)

d) When I subtracted 11 from twice a number, the result was 15
Let, the number be ‘x’
Twice a number is 2x
I subtracted 11 from it, 2x – 11
Result was 15
i.e 2x – 11 = 15
2x = 15 + 11 (Transposing -11 to RHS)
2x = 26
Therefore x = 13 (Dividing both sides by 2)

e) Munna subtracts thrice the number of notebooks he has from 50, he finds the result to be 8.

Let the number of notebooks = x
Thrice the number of notebooks = 3x
Munna subtracts thrice the number of notebooks he has from 50 ,
i.e 50 – 3x
The result is 8
i e 50 – 3x = 8
50 – 8 = 3x (Transposing +8 to LHS and -3x to RHS)
The above equation can be written as 3x = 42
Therefore x = 14 (Dividing both sides by 3)

f) Ibenhal thinks of a number. If she adds 19 to it and divides the sum by 5, she will get 8.

Let the number = x
Add 19 to it; x + 19
Divide the sum by 5 ; $\cfrac { x+19 }{ 5 }$
The result is 8
Therefore $\cfrac { x+19 }{ 5 }$ = 8
Multiply both sides by 5, we get,
x + 19 = 40
x = 40 – 19 (Transposing +19 to RHS)
Therefore x = 21

g) Anwar thinks of a number. If he takes away 7 from of the number, the result is .

Let the number = x
$\cfrac { 5 }{ 2 }$ of the number = $\cfrac { 5x }{ 2 }$
Take away 7 from $\cfrac { 5 }{ 2 }$ of the number; $\cfrac { 5x }{ 2 }$ – 7
Result is $\cfrac { 11 }{ 2 }$
Therefore $\cfrac { 5x }{ 2 }$ – 7 = $\cfrac { 11 }{ 2 }$
$\cfrac { 5x }{ 2 }$ – $\cfrac { 14 }{ 2 }$ = $\cfrac { 11 }{ 2 }$ (Taking LCM)
$\cfrac { 5x-14 }{ 2 }$ = $\cfrac { 11 }{ 2 }$
5x – 14 = 11 (Multiplying both sides by 2)
5x = 11 + 14 (Transposing -14 to RHS)
5x = 25
Therefore x = 5 (Dividing both sides by 5)

2. Solve the following

a) The teacher tells the class that the highest marks obtained by a student in her class are twice the lowest marks plus 7. The highest score is 87. What is the lowest score?

Solution:

Let lowest mark = x
Given highest score equals 87 and it is twice the lowest mark plus 7
87 = 2x + 7
The above equation can be written as 2x + 7 = 87
2x = 87 – 7 (Transposing +7 to RHS)
2x = 80
x = 40 (Dividing both sides by 2)
Therefore the lowest score is 40

b) In an isosceles triangle, the base angles are equal. The vertex angle is 40°. What are the base angles of the triangle? (Remember, the sum of three angles of a triangle is 180°).

Solution:

Given:
Vertex angle = 40°
Triangle is an isosceles triangle

Let the base angles = b^oTherefore, b^o+ b^o+ 40^o = 180^o   (Sum of three angles of a triangle is 180°)
2b^o + 40^o = 180^o2b^o = 180^o – 40^o    (Transposing +40 to RHS)
2b^o = 140^ob^o = 70^o   (Dividing 2 on both sides)
The base angles of the triangle is 70^o

c) Sachin scored twice as many runs as Rahul. Together, their runs fell two short of a double century. How many runs did each one score?

Solution:

Let Rahul’s score = x
Therefore Sachin’s score = 2x
Two short of a double century is 200 – 2 = 198
Since together their runs fell two short of a double century
2x + x = 198
3x = 198
x = 66 which is Rahul’s score.
Sachin’s score is 2 x 66 = 132

3. Solve the following:

(i) Irfan says that he has 7 marbles more than five times the marbles Parmit has. Irfan has 37 marbles. How many marbles does Parmit have?

Solution:

Let number of marbles Parmit has = x
Number of marbles Irfan has = 5x + 7
i.e 5x + 7 = 37
5x = 37 – 7 (Transposing +7 to RHS)
5x = 30
x = 6 is the number of marbles Parmit has.

(ii) Laxmi’s father is 49 years old. He is 4 years older than three times Laxmi’s age. What is Laxmi’s age?

Solution:

Let Laxmi’s age = x
Laxmi’s father’s age is 3x + 4 = 49
3x = 49 – 4 (Transposing +4 to RHS)
3x = 45
x = 15 is Laxmi’s age.

(iii) People of Sundargram planted trees in the village garden. Some of the trees were fruit trees. The number of non-fruit trees were two more than three times the number of fruit trees. What was the number of fruit trees planted if the number of non-fruit trees planted was 77?

Solution:

Let the number of fruit trees = x
Number of non-fruit trees planted = 77 (Given)
The number of non-fruit trees were two more than three times the number of fruit trees , therefore
77 = 3x + 2
i.e 3x + 2 = 77
3x = 77 – 2 (Transposing +2 to RHS)
3x = 75
x = 25 is the number of fruit trees planted.

4. Solve the following riddle:

I am a number,
Tell my identity!
Take me seven times over
And add a fifty!
To reach a triple century
You still need forty!

Solution:

Let the number = x
Take the number seven times over and add a fifty i.e 7x + 50
To reach a triple century you still need forty i.e 300 = 7x + 50 + 40
7x + 90 = 300
7x = 300 – 90 (Transposing +90 to RHS)
7x = 210
x = 30 is the number

This Chapter contains the Exercises relating to the following topics , which are discussed in Chapter 4 – Simple Equations Class 7 NCERT book : –

4.1 A MIND-READING GAME!
4.2 SETTING UP OF AN EQUATION
4.3 REVIEW OF WHAT WE KNOW
4.4 WHAT EQUATION IS?
4.4.1 Solving an Equation
4.5 MORE EQUATIONS
4.6 FROM SOLUTION TO EQUATION
4.7 APPLICATIONS OF SIMPLE EQUATIONS TO PRACTICAL SITUATIONS

Download NCERT Solutions for Class 7 Maths Chapter 4 – Simple Equations

NCERT Solutions for Class 7 Maths Chapter 4 – Simple Equations

NCERT Solutions for Class 7 Maths Chapter 4 Exercise 4.1

NCERT Solutions for Class 7 Maths Chapter 4 Exercise 4.2

NCERT Solutions for Class 7 Maths Chapter 4 Exercise 4.3

NCERT Solutions for Class 7 Maths Chapter 4 Exercise 4.4

NCERT Solutions for Class 7 Maths Chapter 4 Exercise 4.1

NCERT Solutions for Class 7 Maths Chapter 4 Exercise 4.2

NCERT Solutions for Class 7 Maths Chapter 4 Exercise 4.3

NCERT Solutions for Class 7 Maths Chapter 4 Exercise 4.4

NCERT Solutions for Class 7

CBSE Notes for Class 7

Worksheets for Class 7

Leave a Comment Cancel reply