Class 7 Maths NCERT Solutions Chapter 14 – Symmetry comprises of the 3 Exercises
This Chapter contains the Exercises relating to the following topics , which are discussed in Chapter 14 – Symmetry Class 7 NCERT book : –
- 14.1 INTRODUCTION
- 14.2 LINES OF SYMMETRY FOR REGULAR POLYGONS
- 14.3 ROTATIONAL SYMMETRY
- 14.4 LINE SYMMETRY AND ROTATIONAL SYMMETRY
NCERT Solutions for Class 7 Maths Chapter 14 Exercise 14.1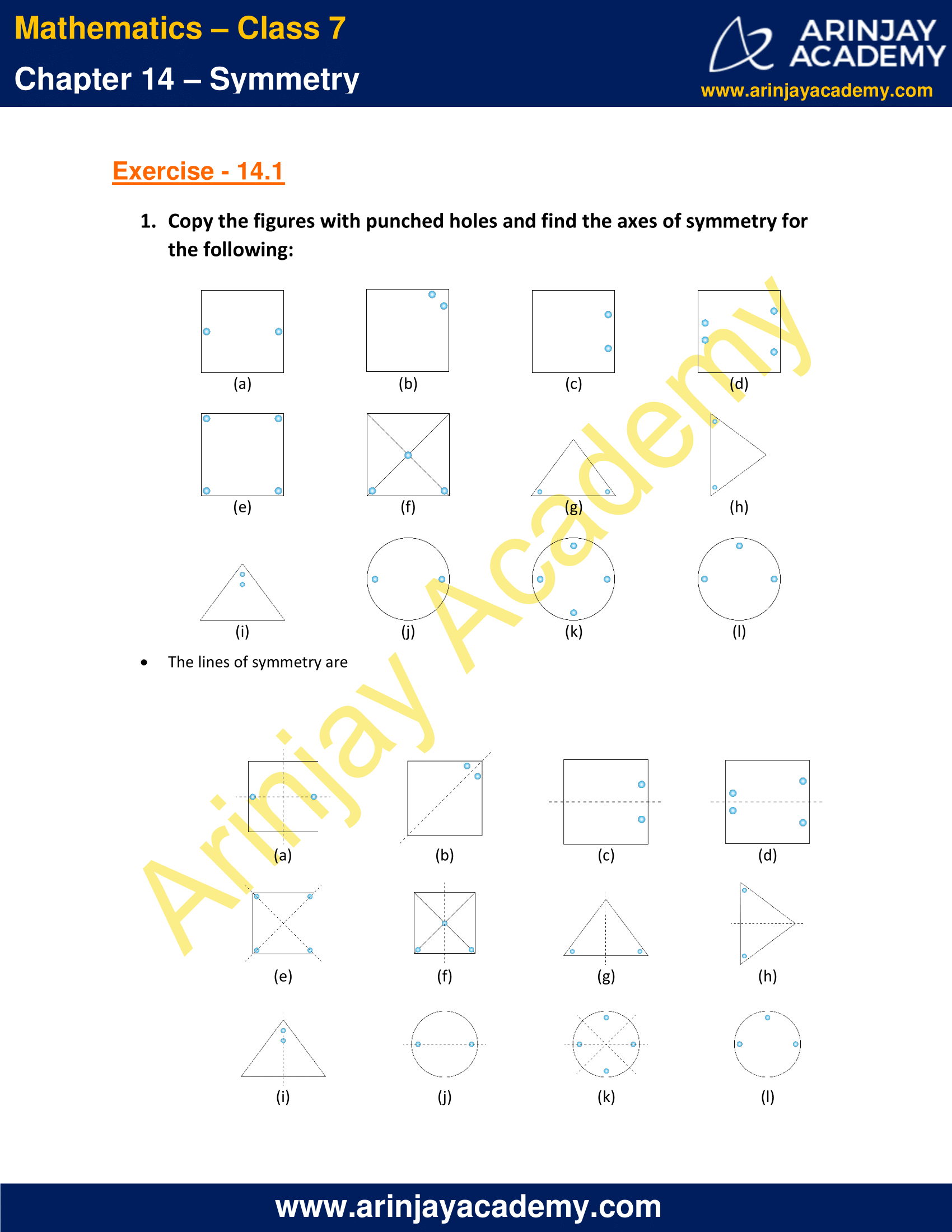
NCERT Solutions for Class 7 Maths Chapter 14 Exercise 14.2
NCERT Solutions for Class 7 Maths Chapter 14 Exercise 14.3
NCERT Solutions for Class 7 Maths Chapter 14 Exercise 14.1
1. Copy the figures with punched holes and find the axes of symmetry for the following:
Solution:
The lines of symmetry are
2. Given the line(s) of symmetry, find the other hole(s):
Solution:
According to the line of symmetry, holes should be present as shown in the figures
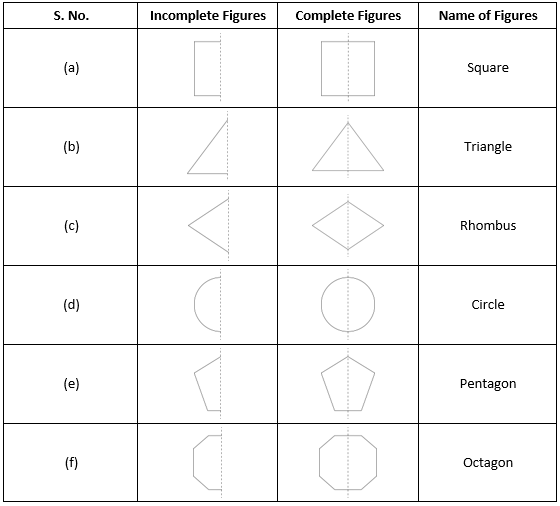
3. In the following figures, the mirror line (i.e., the line of symmetry) is given as a dotted line. Complete each figure performing reflection in the dotted (mirror) line. (You might perhaps place a mirror along the dotted line and look into the mirror for the image). Are you able to recall the name of the figure you complete?
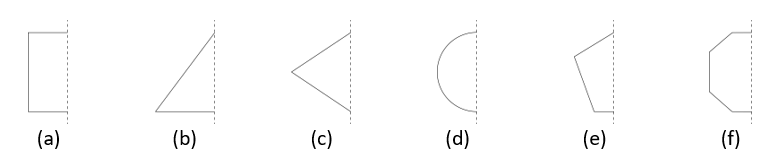
Solution:
The complete figures are
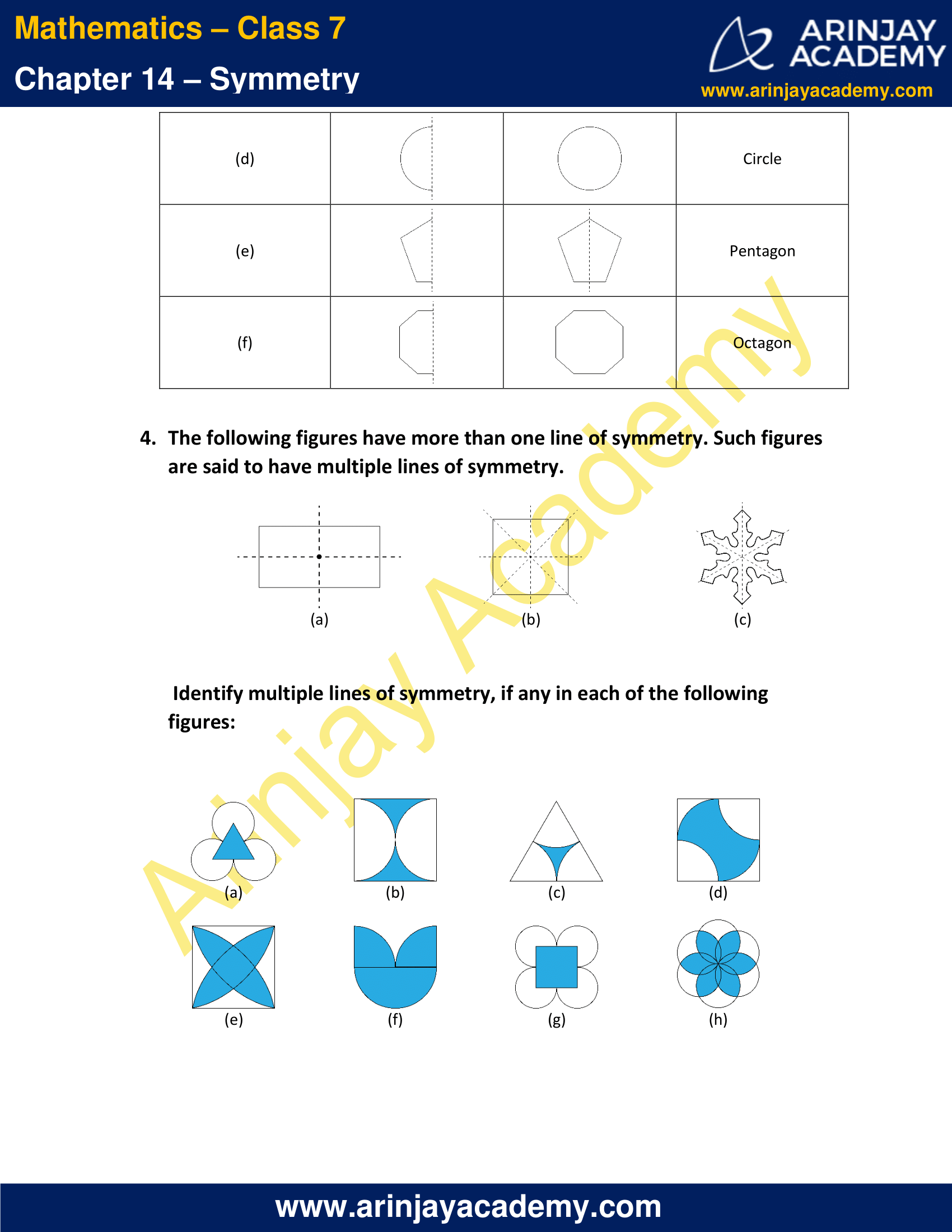
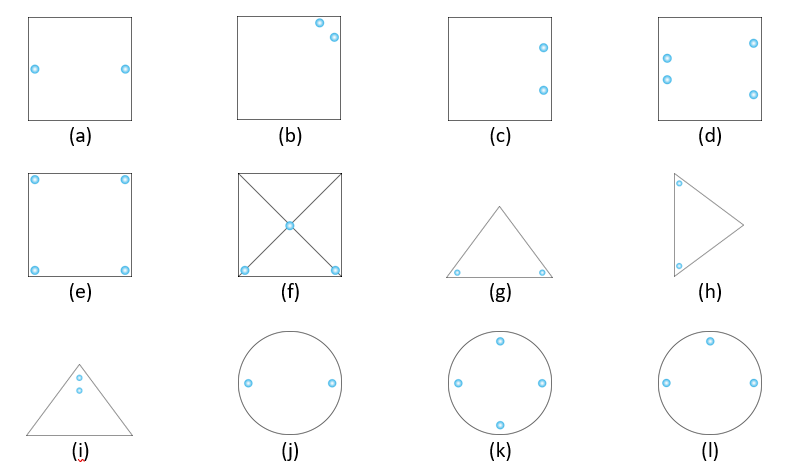
4. The following figures have more than one line of symmetry. Such figures are said to have multiple lines of symmetry.
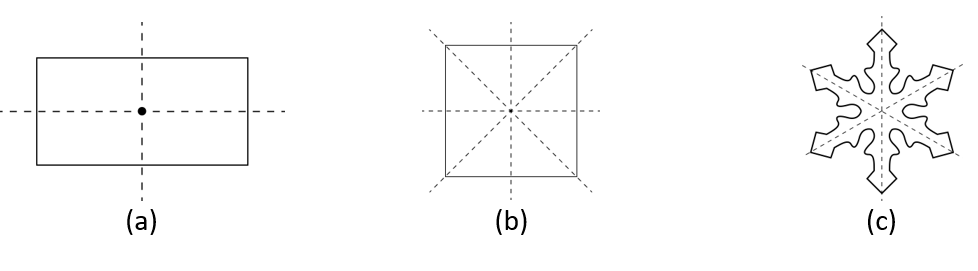Identify multiple lines of symmetry, if any in each of the following figures:
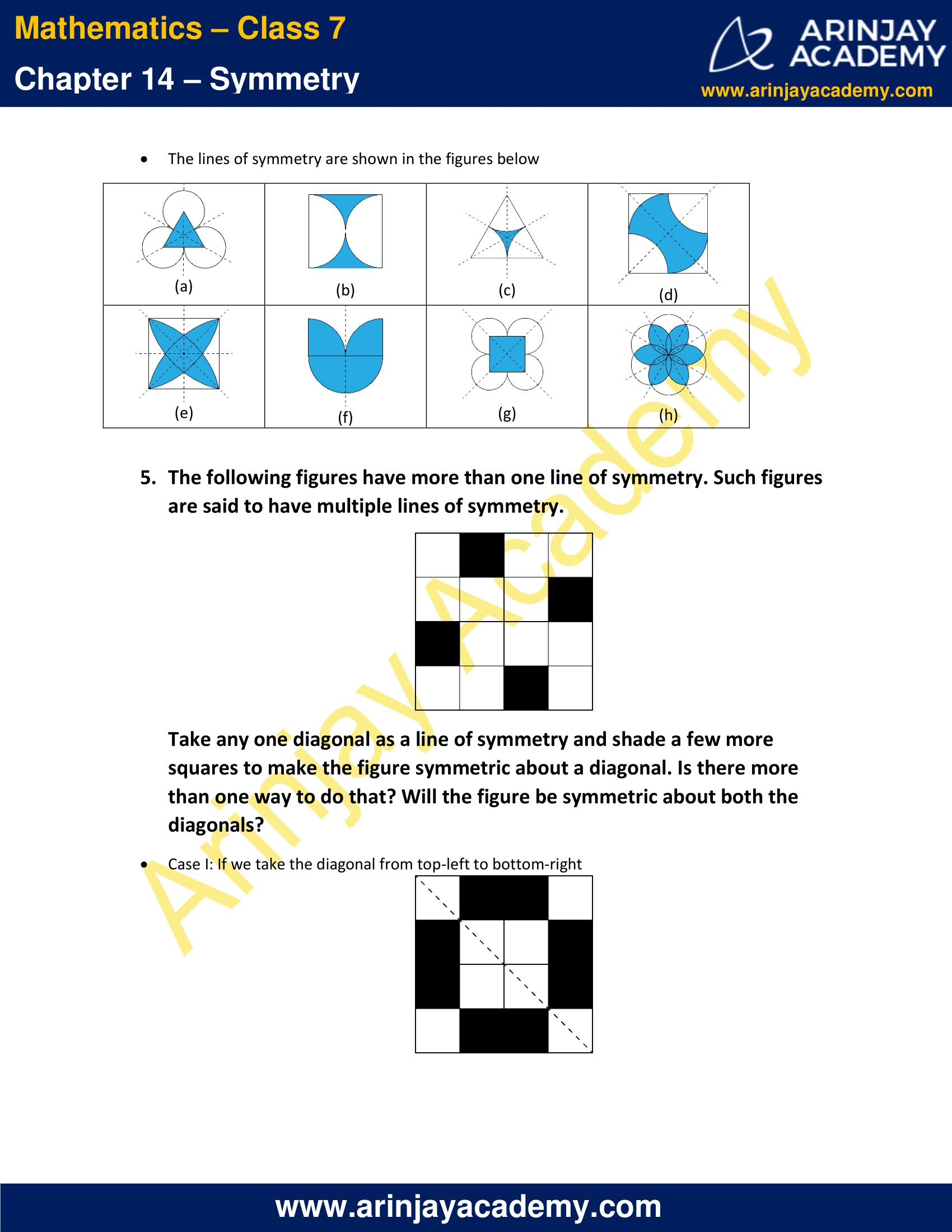
Solution:
The lines of symmetry are shown in the figures below
5. The following figures have more than one line of symmetry. Such figures are said to have multiple lines of symmetry.
Take any one diagonal as a line of symmetry and shade a few more squares to make the figure symmetric about a diagonal. Is there more than one way to do that? Will the figure be symmetric about both the diagonals?
Solution:
Case I: If we take the diagonal from top-left to bottom-right
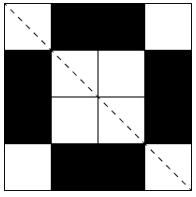
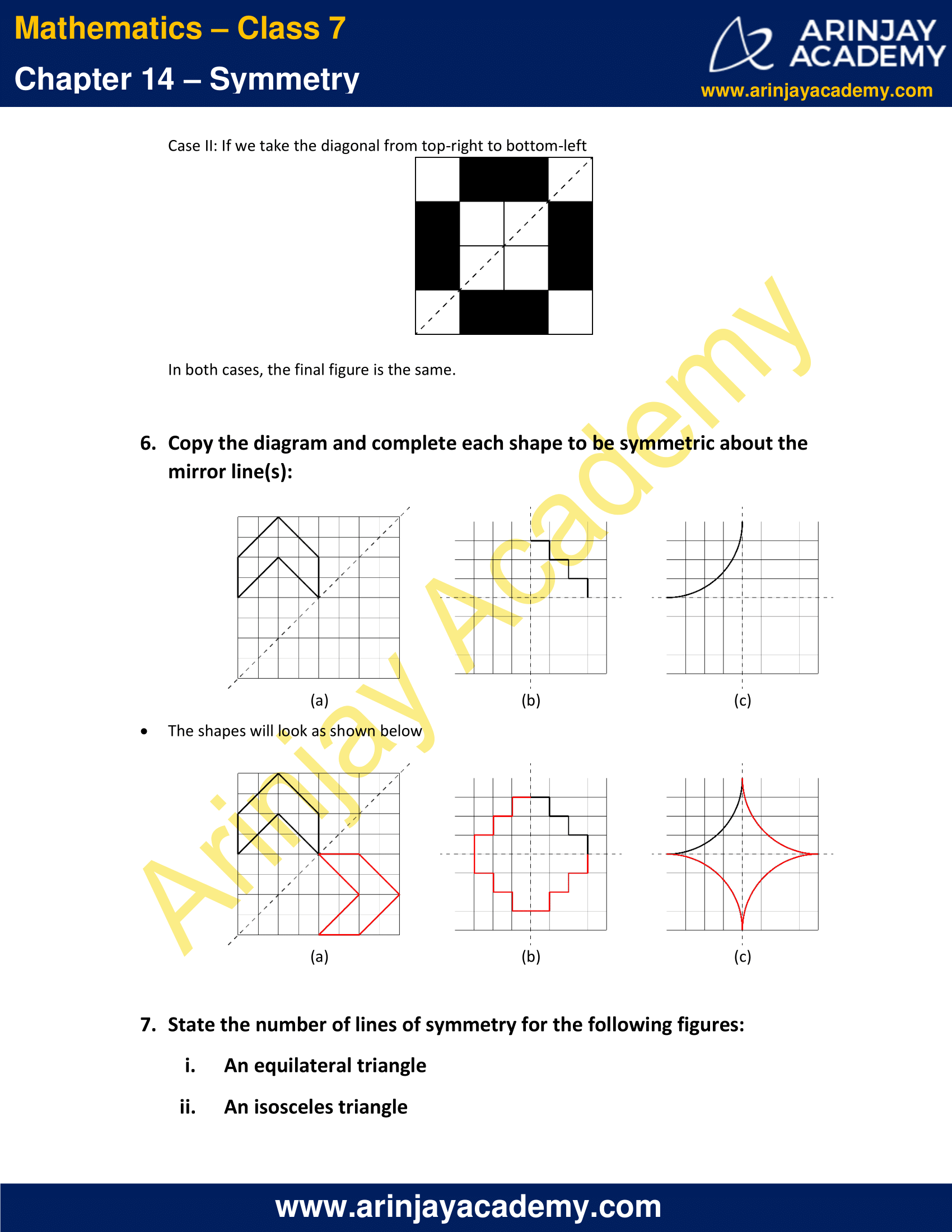
Case II: If we take the diagonal from top-right to bottom-left
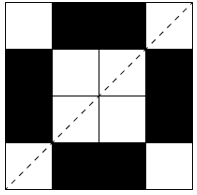
In both cases, the final figure is the same.
6. Copy the diagram and complete each shape to be symmetric about the mirror line(s):
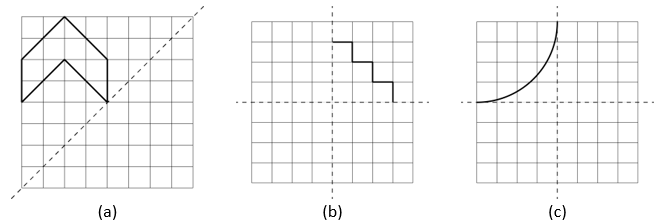
Solution:
The shapes will look as shown below
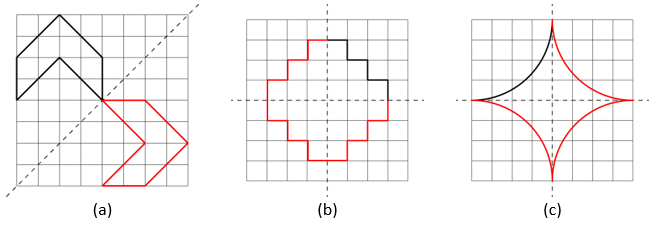
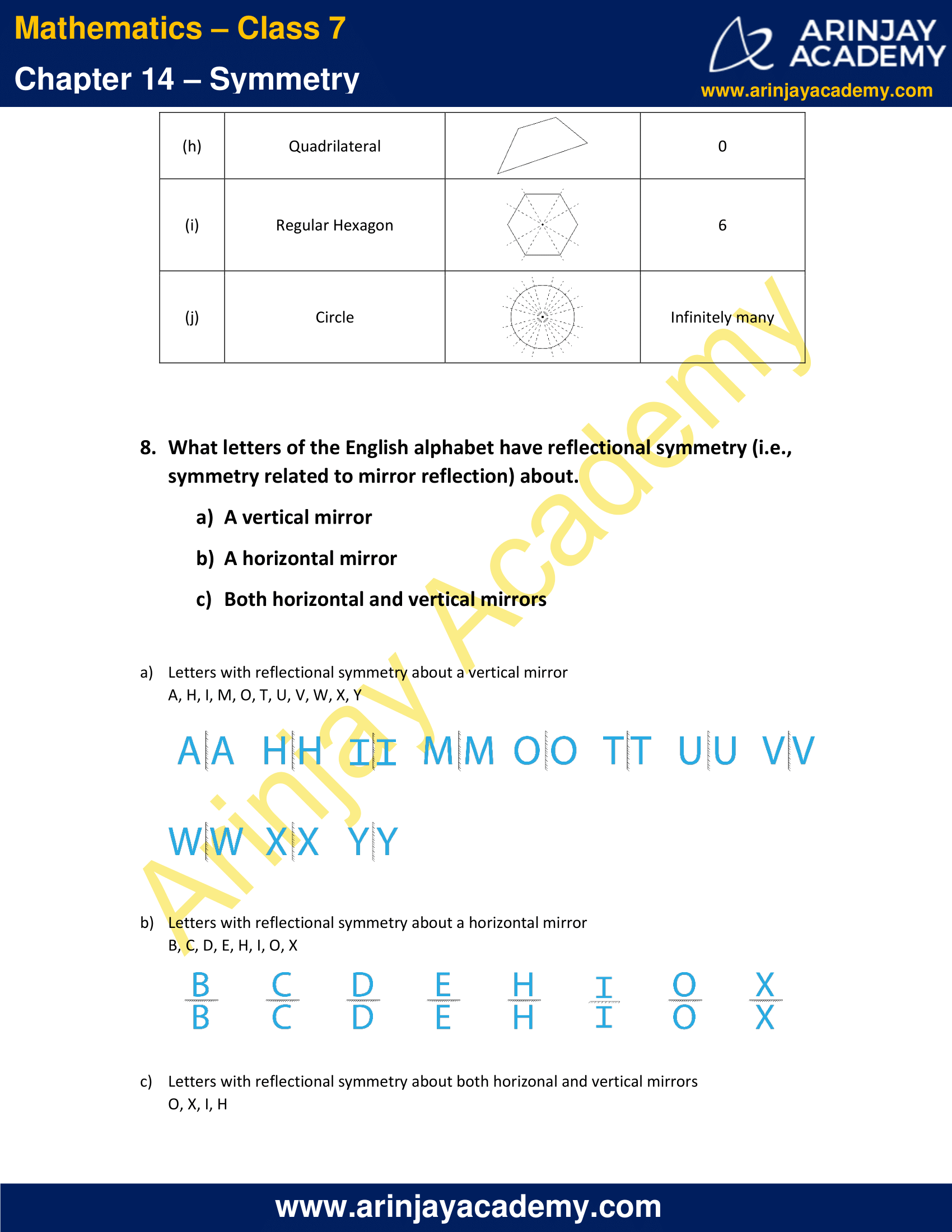
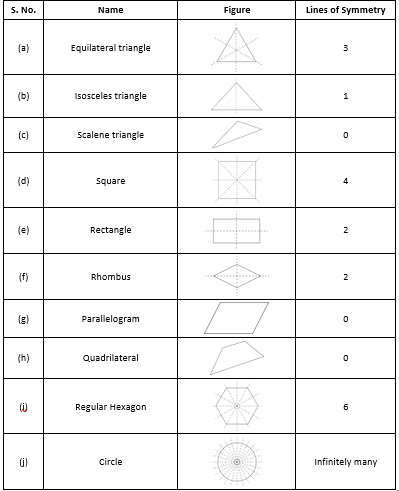
7. State the number of lines of symmetry for the following figures:
a) An equilateral triangle
b) An isosceles triangle
c) A scalene triangle
d) A square
e) A rectangle
f) A rhombus
g) A parallelogram
h) A quadrilateral
i) A regular hexagon
j) A circle
Solution:
The number of lines of symmetry are as follows:
8. What letters of the English alphabet have reflectional symmetry (i.e., symmetry related to mirror reflection) about.
a) A vertical mirror
b) A horizontal mirror
c) Both horizontal and vertical mirrors
a) Letters with reflectional symmetry about a vertical mirror
A, H, I, M, O, T, U, V, W, X, Y
b) Letters with reflectional symmetry about a horizontal mirror
B, C, D, E, H, I, O, X
c) Letters with reflectional symmetry about both horizonal and vertical mirrors
O, X, I, H
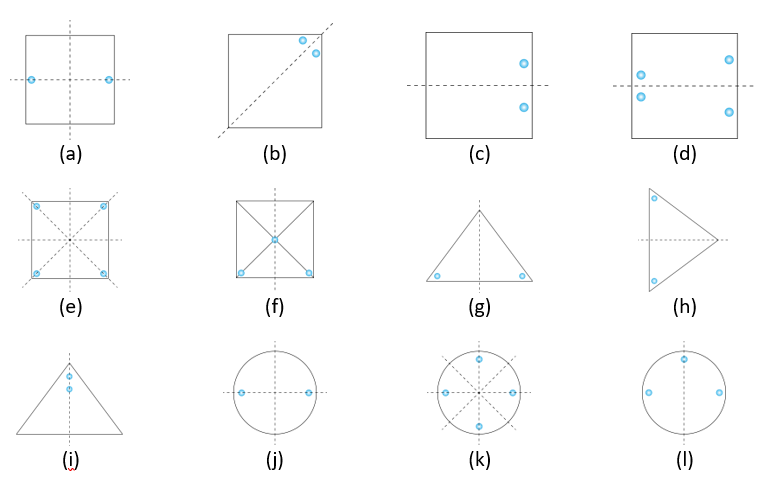
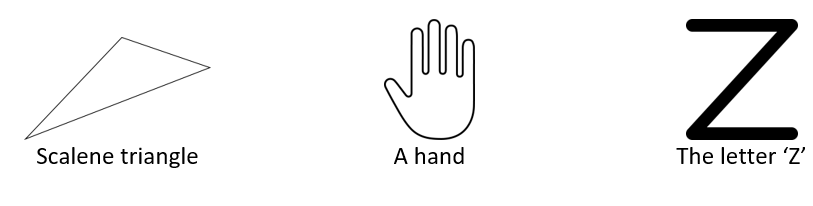
9. Give three examples of shapes with no line of symmetry.
Solution:
Examples of shapes with no lines of symmetry are
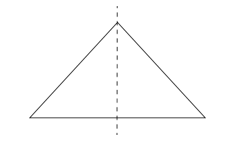
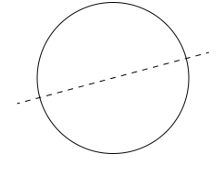
10. What other names can you give to the line of symmetry of
a) An isosceles triangle?
b) A circle?
Solution:
a) The line of symmetry of an isosceles triangle is the median of the triangle.
b) The line of symmetry of a circle is the diameter.
NCERT Solutions for Class 7 Maths Chapter 14 Exercise 14.2
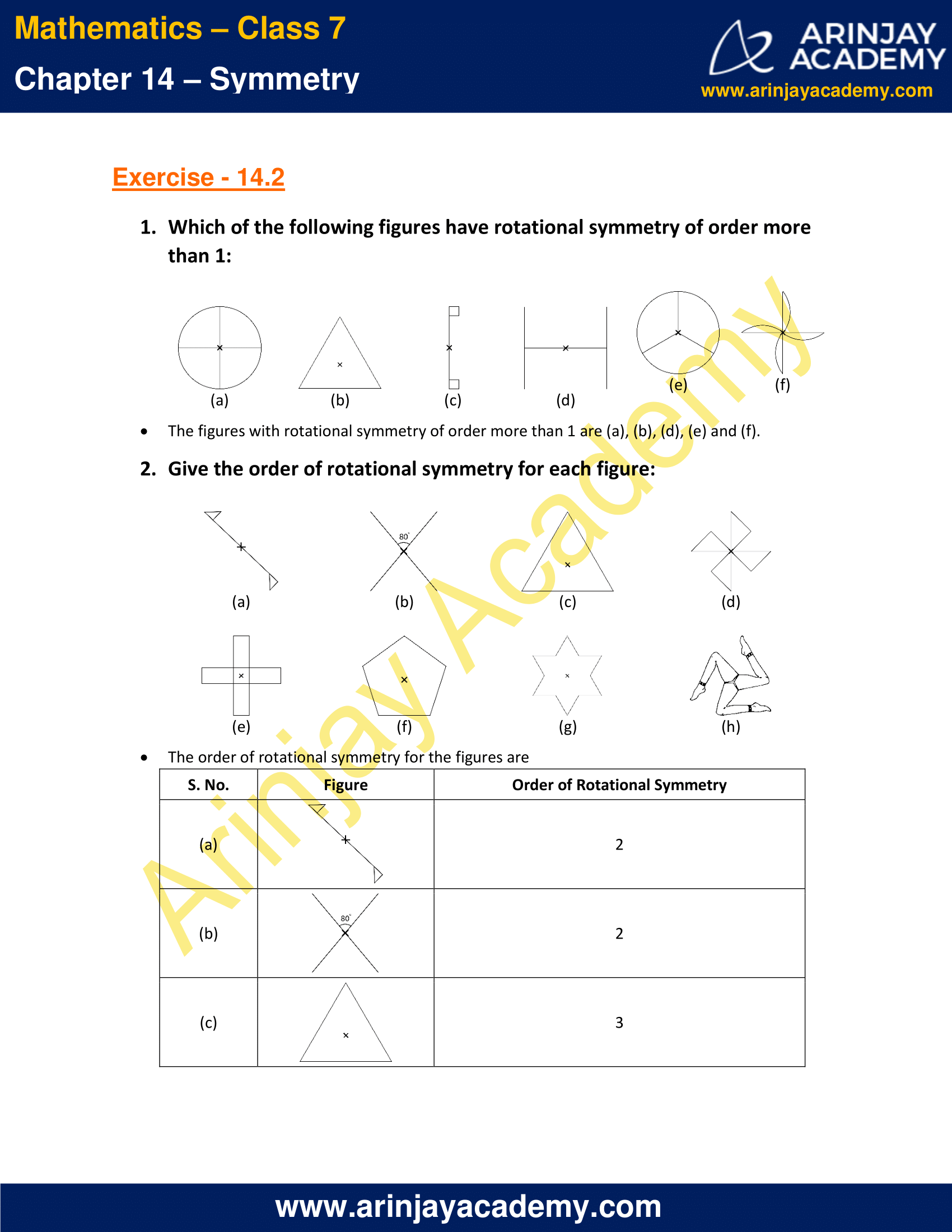
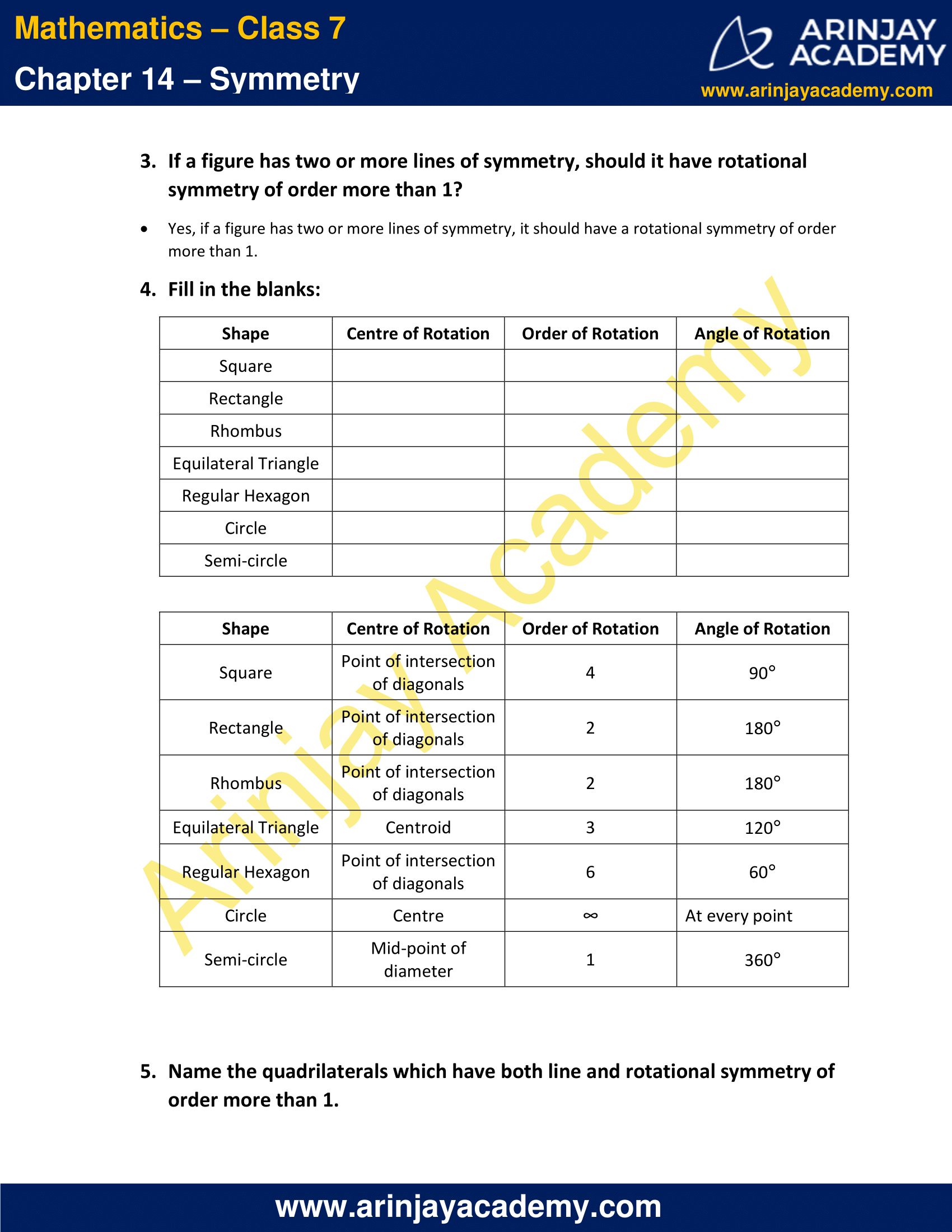
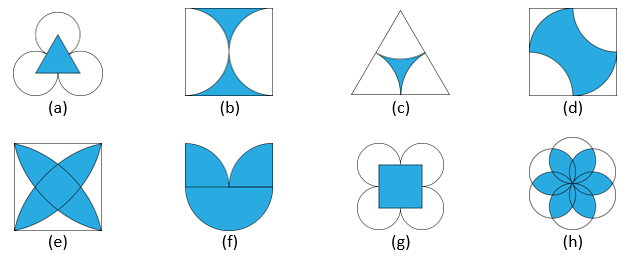
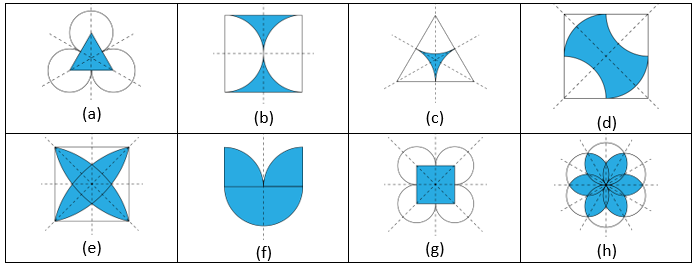
1. Which of the following figures have rotational symmetry of order more than 1:
Solution:
The figures with rotational symmetry of order more than 1 are (a), (b), (d), (e) and (f).
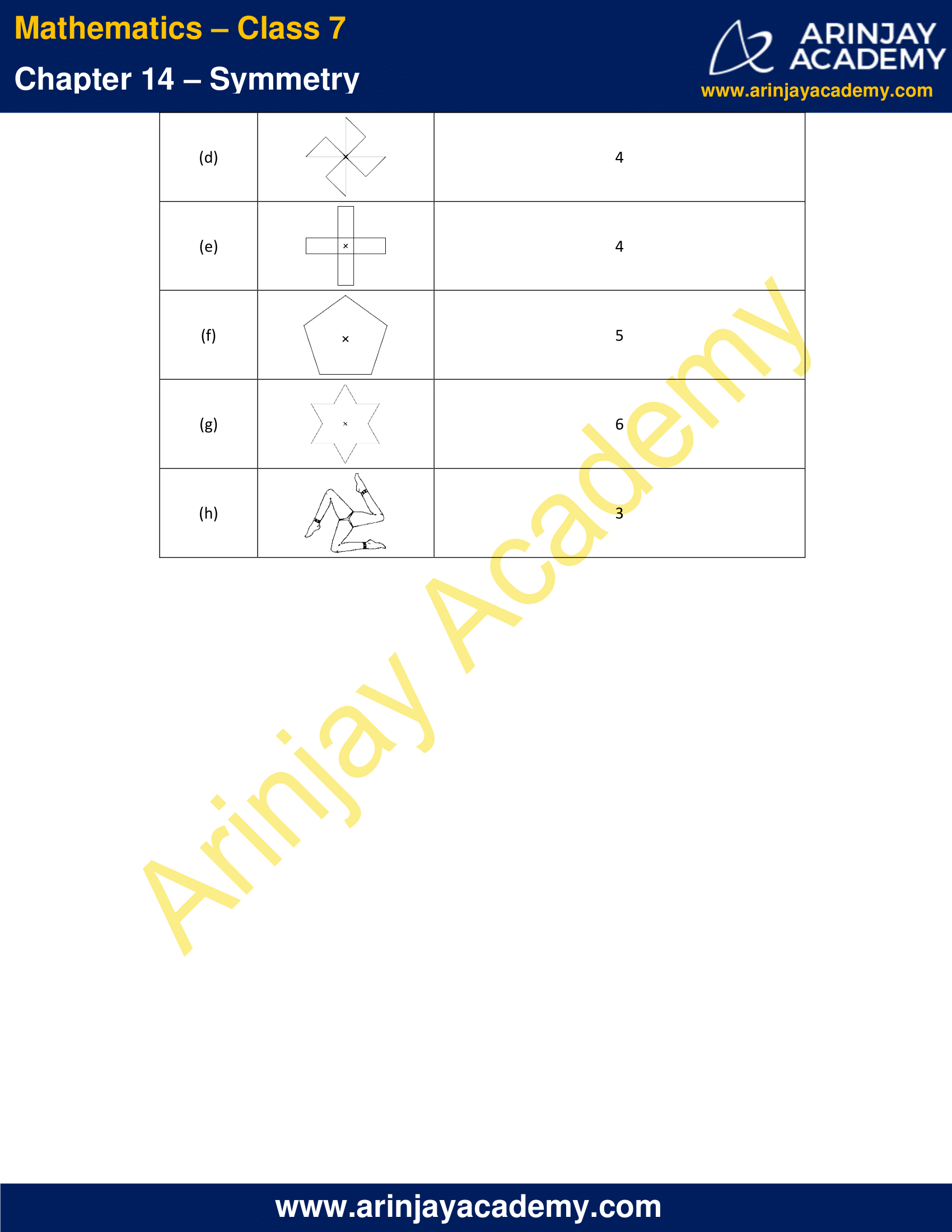
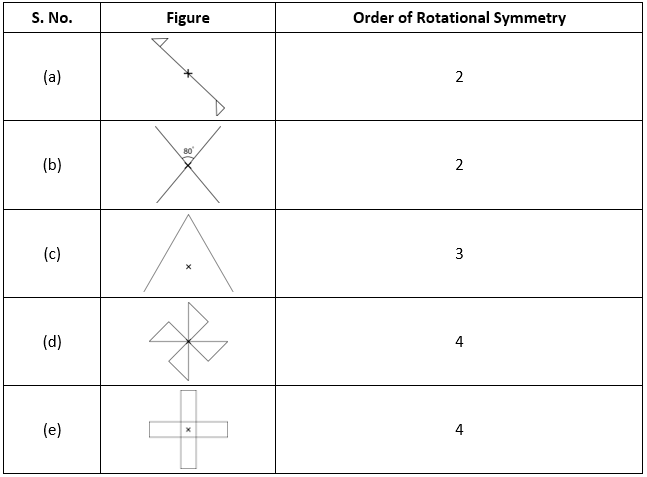
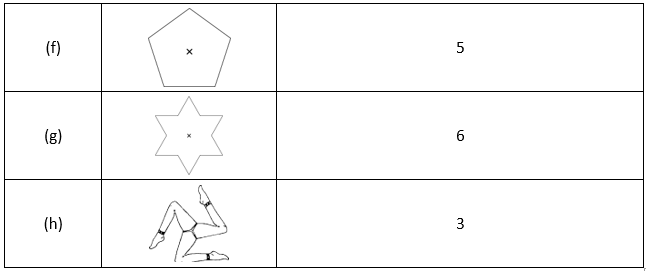
2. Give the order of rotational symmetry for each figure:
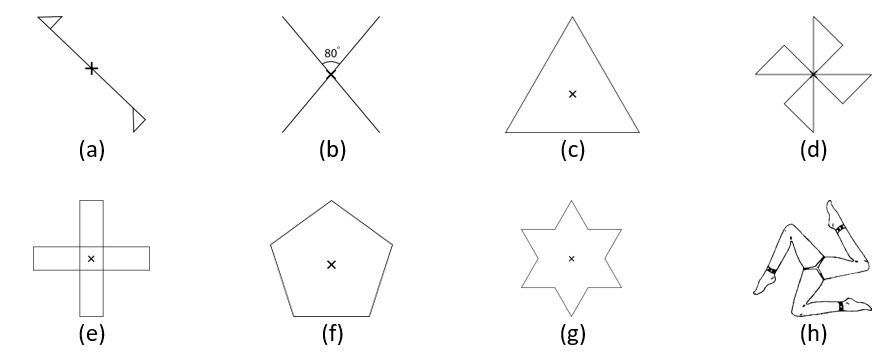
Solution:
The order of rotational symmetry for the figures are
NCERT Solutions for Class 7 Maths Chapter 14 Exercise 14.3
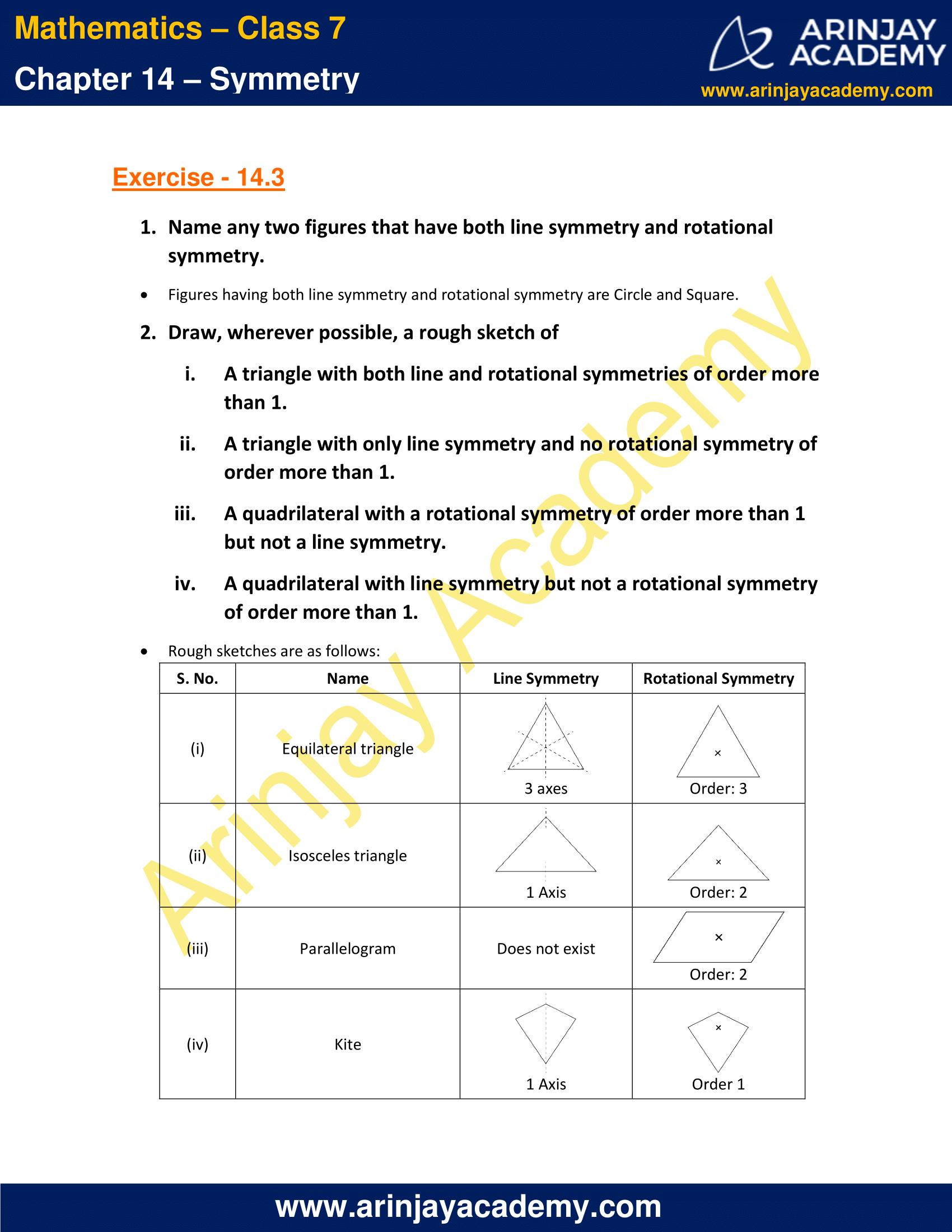
1. Name any two figures that have both line symmetry and rotational symmetry.
Solution:
Figures having both line symmetry and rotational symmetry are Circle and Square.
2. Draw, wherever possible, a rough sketch of
i. A triangle with both line and rotational symmetries of order more than 1.
ii. A triangle with only line symmetry and no rotational symmetry of order more than 1.
iii. A quadrilateral with a rotational symmetry of order more than 1 but not a line symmetry.
iv. A quadrilateral with line symmetry but not a rotational symmetry of order more than 1.
Solution:
Rough sketches are as follows:
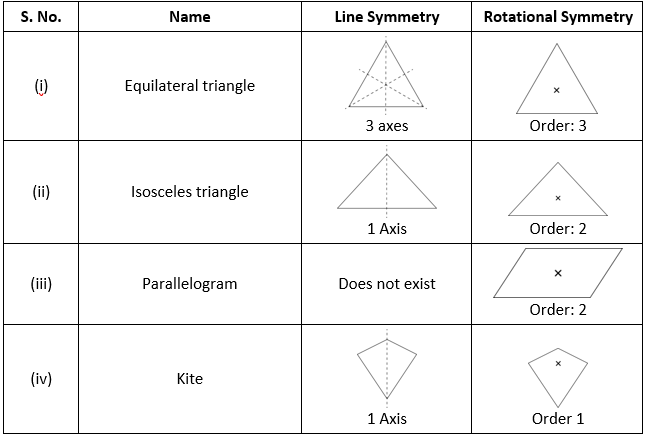
3. If a figure has two or more lines of symmetry, should it have rotational symmetry of order more than 1?
Solution:
Yes, if a figure has two or more lines of symmetry, it should have a rotational symmetry of order more than 1.
4. Fill in the blanks:
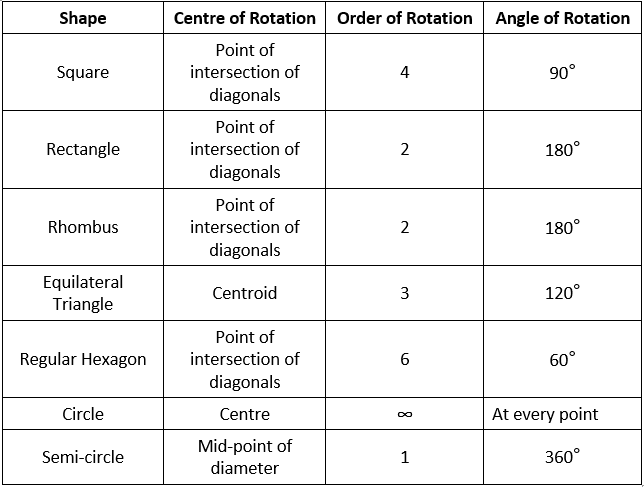
Solution:
5. Name the quadrilaterals which have both line and rotational symmetry of order more than 1.
Solution:
Square have both line and rotational symmetry of order more than 1.
6. After rotating by 60° about a centre, a figure looks exactly the same as its original position. At what other angles will this happen for the figure?
Solution:
If after rotating a figure by any angle, it looks exactly the same as its original position, then, this will happen at all angles that are the multiples of the former angle.
Therefore, in this case, it will happen for all the angles that are multiples of 60°, i.e. 120°, 180°, 240° and so on.
7. Can we have a rotational symmetry of order more than 1 whose angle of rotation is
i. 45°
ii. 17°
Solution:
i. Order of rotation = 360°/Angle of Rotation = 360°/45° = 8
Here, the order of rotation is a natural number.
Hence, 45° can be the angle of rotation, then symmetry of order is possible.
ii. Order of rotation = 360°/Angle of Rotation = 360°/17° = 27.176…
Here, the order of rotation is not a natural number.
Hence, 17° cannot be the angle of rotation, then symmetry of order is not possible.
With this we come to the end of NCERT Solutions for Class 7 Maths Chapter 14 Symmetry. We hope these helped you study your subject.
Download NCERT Solutions for Class 7 Maths Chapter 14 – Symmetry
