Arinjay Academy » Maths Class 7 » NCERT Solutions for Class 7 Maths Chapter 13 – Exponents and Powers

NCERT Solutions for Class 7 Maths Chapter 13 – Exponents and Powers

Class 7 Maths NCERT Solutions Chapter 13 – Exponents and Powers comprises of the 4 Exercises

Exercise 13.1
Exercise 13.2
Exercise 13.3

NCERT Solutions for Class 7 Maths Chapter 13 Exercise 13.1

NCERT Solutions for Class 7 Maths Chapter 13 Exercise 13.2

NCERT Solutions for Class 7 Maths Chapter 13 Exercise 13.3

NCERT Solutions for Class 7 Maths Chapter 13 Exercise 13.1

1. Find the value of:

i) 2⁶ii) 9³iii) 11²iv) 5⁴

i) 2⁶ = 2 × 2 × 2 × 2 × 2 × 2 = 64
ii) 9³ = 9 × 9 × 9 = 729
iii) 11² = 11 × 11 = 121
iv) 5⁴ = 5 × 5 × 5 × 5 = 625

2. Express the following in exponential form:

i) 6 × 6 × 6 × 6
ii) t × t
iii) b × b × b × b
iv) 5 × 5 × 7 × 7 × 7
v) 2 × 2 × a × a
vi) a × a × a × c × c × c × c × d

i) 6 × 6 × 6 × 6 = 6⁴ii) t × t = t²iii) b × b × b × b = b⁴iv) 5 × 5 × 7 × 7 × 7 = 5² × 7³v) 2 × 2 × a × a = 2² × a²vi) a × a × a × c × c × c × c × d = a³ × c⁴ × d

3. Express each of the following numbers using exponential notation:

i) 512
ii) 343
iii) 729
iv) 3125

i) 512 = 2 × 256
= 2 × 2 × 128
= 2 × 2 × 2 × 64
= 2 × 2 × 2 × 2 × 32
= 2 × 2 × 2 × 2 × 2 × 16
= 2 × 2 × 2 × 2 × 2 × 2 × 8
= 2 × 2 × 2 × 2 × 2 × 2 × 2 × 4
= 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
= 2⁹

ii) 343 = 7 × 49
= 7 × 7 × 7
= 7³

iii) 729 = 3 × 243
= 3 × 3 × 81
= 3 × 3 × 3 × 27
= 3 × 3 × 3 × 3 × 9
= 3 × 3 × 3 × 3 × 3 × 3
= 3⁶

iv) 3125 = 5 × 625
= 5 × 5 × 125
= 5 × 5 × 5 × 25
= 5 × 5 × 5 × 5 × 5
= 5⁵

4. Identify the greater number, wherever possible, in each of the following?

i) 4³ or 3⁴ii) 5³ or 3⁵iii) 2⁸ or 8²iv) 100² or 2¹⁰⁰v) 2¹⁰ or 10²

i) 4³ = 4 × 4 × 4 = 64
3⁴ = 3 × 3 × 3 × 3 = 81
∵ 81 > 64
∴ 3⁴ > 4³

ii) 5³ = 5 × 5 × 5 = 125
3⁵ = 3 × 3 × 3 × 3 × 3 = 243
∵ 243 > 125
∴ 3⁵ > 5³

iii) 2⁸ = 2 × 2 × 2 × 2 × 2 × 2 × 2 ×2 = 256
8² = 8 × 8 = 64
∵ 256 > 64
∴ 2⁸ > 8²

iv) 100² = 100 × 100 = 10,000
2¹⁰⁰ = 2 × 2 × 2 × 2 × 2 × 2 × 2 ×2 × 2 × 2 × 2 × 2 × 2 × 2 × 2⁸⁶ = 16,384 × 2⁸⁶∵ 16,384 × 2⁸⁶ > 10,000
∴ 2¹⁰⁰ > 100²

v) 2¹⁰ = 2 × 2 × 2 × 2 × 2 × 2 × 2 ×2 × 2 × 2 = 1024
10² = 10 × 10 = 100
∵ 1024 > 100
∴ 2¹⁰ > 10²

5. Express each of the following as product of powers of their prime factors:

i) 648
ii) 405
iii) 540
iv) 3,600

i) 648 = 2 × 2 × 2 × 3 × 3 × 3 × 3
= 2³ × 3⁴

ii) 405 = 5 × 3 × 3 × 3 × 3
= 5 × 3⁴

iii) 540 = 2 × 2 × 3 × 3 × 3 × 5
= 2² × 3³ × 5

iv) 3,600 = 2 × 2 × 2 × 2 × 3 × 3 × 5 × 5
= 2⁴ × 3² × 5²

6. Simplify:

i) 2 × 10³ii) 7² × 2²iii) 2³ × 5
iv) 3 × 4⁴v) 0 × 10²vi) 5² × 3³vii) 2⁴ × 3²viii) 3² × 10⁴

i) 2 × 10³ = 2 × 10 × 10 × 10 = 2,000
ii) 7² × 2² = 7 × 7 × 2 × 2 = 196
iii) 2³ × 5 = 8 × 5 = 40
iv) 3 × 4⁴ = 3 × 4 × 4 × 4 × 4 = 768
v) 0 × 10² = 0 × 10 × 10 = 0
vi) 5² × 3³ = 5 × 5 × 3 × 3 × 3 = 675
vii) 2⁴ × 3² = 2 × 2 × 2 × 2 × 3 × 3 = 144
viii) 3² × 10⁴ = 3 × 3 × 10 × 10 × 10 × 10 = 90,000

7. Simplify:

i) (-4)³ii) (-3) × (-2)³iii) (-3)² × (-5)²iv) (-2)³ × (-10)³

i) (-4)³ = (-4) × (-4) × (-4) = -64
ii) (-3) × (-2)³ = (-3) × (-2) × (-2) × (-2) = 24
iii) (-3)² × (-5)² = (-3) × (-3) × (-5) × (-5) = 225
iv) (-2)³ × (-10)³ = (-2) × (-2) × (-2) × (-10) × (-10) × (-10) = 8,000

8. Compare the following numbers:

i) 2.7 × 10¹²; 1.5 × 10⁸ii) 4 × 10¹⁴; 3 × 10¹⁷

i) 2.7 × 10¹² has more digits than 1.5 × 10⁸Hence, 2.7 × 10¹² > 1.5 × 10⁸

ii) 4 × 10¹⁴ has less digits than 3 × 10¹⁷Hence, 4 × 10¹⁴ < 3 × 10¹⁷

NCERT Solutions for Class 7 Maths Chapter 13 Exercise 13.2

1. Using laws of exponents, simplify and write the answer in exponential form:

i) 3² × 3⁴ × 3⁸ii) 6¹⁵ ÷ 6¹⁰iii) a³ × a²iv) 7^x × 7²v) (5²)³÷ 5³vi) 2⁵ × 5⁵vii) a⁴ × b⁴viii) (3⁴)³ix) (2²⁰ ÷ 2¹⁵) × 2³x) 8^t ÷ 8²

i) 3² × 3⁴ × 3⁸
= 3^{(2 + 4 + 8)} (∵ a^m × aⁿ = a^{m + n})
= 3¹⁴

ii) 6¹⁵ ÷ 6¹⁰
= 6^{(15 – 10)} (∵ a^m ÷ aⁿ = a^{m – n})
= 6⁵

iii) a³ × a²
= a^{(3 + 2)} (∵ a^m × aⁿ = a^{m + n})
= a⁵

iv) 7^x × 7²
= 7^{(x + 2)} (∵ a^m × aⁿ = a^{m + n})

v) (5²)³÷ 5³
= 5⁶ ÷ 5³ (∵ (a^m)ⁿ = a^mn)
= 5^{(6 – 3)} (∵ a^m ÷ aⁿ = a^{m – n})
= 5³

vi) 2⁵ × 5⁵
= (2 × 5)⁵ (∵ a^m × b^m = (ab)^m)
= 10⁵

vii) a⁴ × b⁴
= (a × b)⁴ (∵ a^m × b^m = (ab)^m)
= (ab)⁴

viii) (3⁴)³
= 3^{4 × 3} (∵ (a^m)ⁿ = a^mn)
= 3¹²

ix) (2²⁰ ÷ 2¹⁵) × 2³
= 2^{(20 – 15)} × 2³ (∵ a^m ÷ aⁿ = a^{m – n})
= 2⁵ × 2³= 2^{(5 + 3)} (∵ a^m × aⁿ = a^{m + n})
= 2⁸

x) 8^t ÷ 8²
= 8^{(t – 2)} (∵ a^m ÷ aⁿ = a^{m – n})

2. Simplify and express each of the following in exponential form:

i) $\cfrac { 2^{ 3 }\times 3^{ 4 }\times 4 }{ 3\times 32 }$
ii) ((5²)³ × 5⁴) ÷ 5⁷iii) 25⁴ ÷ 5³iv) $\cfrac { 3\times 7^{ 2 }\times 11^{ 8 } }{ 21\times 11^{ 3 } }$
v) $\cfrac { 3^{ 7 } }{ 3^{ 4 }\times 3^{ 3 } }$
vi) 2⁰ + 3⁰+ 4⁰vii) 2⁰ × 3⁰× 4⁰viii) (3⁰ + 2⁰) × 5⁰ix) $\cfrac { 2^{ 8 }\times a^{ 5 } }{ 4^{ 3 }\times a^{ 3 } }$
x) $\cfrac { a^{ 5 } }{ a^{ 3 } } \times a^{ 8 }$
xi) $\cfrac { 4^{ 5 }\times a^{ 8 }b^{ 3 } }{ 4^{ 5 }\times a^{ 5 }b^{ 2 } }$
xii) (2³ × 2)²

i) $\cfrac { 2^{ 3 }\times 3^{ 4 }\times 4 }{ 3\times 32 }$
= $\cfrac { 2^{ 3 }\times 3^{ 4 }\times 2^{ 2 } }{ 3\times 2^{ 5 } }$
= $\cfrac { 2^{ 5 }\times 3^{ 4 } }{ 3\times 2^{ 5 } }$ (∵ a^m × aⁿ = a^{m + n})
= 2^{(5 – 5)} × 3^{(4 – 1)} (∵ $\cfrac { a^{ m } }{ a^{ n } }$ = a^{m – n})
= 2⁰ × 3³= 3³ (∵ a⁰ = 1)

ii) ((5²)³ × 5⁴) ÷ 5⁷
= (5^2×3 × 5⁴) ÷ 5⁷ (∵ (a^m)ⁿ = a^mn)
= (5⁶ x 5⁴) ÷ 5⁷= 5^{(6 + 4)} ÷ 5⁷ (∵ a^m × aⁿ = a^{m + n})
= 5¹⁰ ÷ 5⁷= 5^{(10 – 7)} (∵ $\cfrac { a^{ m } }{ a^{ n } }$ = a^{m – n})
= 5³

iii) 25⁴ ÷ 5³ = (5²)⁴ ÷ 5³= 5^{(2 × 4)} ÷ 5³ (∵ (a^m)ⁿ = a^mn)
= 5⁸ ÷ 5³= 5^{(8 – 3)} (∵ $\cfrac { a^{ m } }{ a^{ n } }$ = a^{m – n})
= 5⁵

iv) $\cfrac { 3\times 7^{ 2 }\times 11^{ 8 } }{ 21\times 11^{ 3 } }$
= $\cfrac { 3\times 7^{ 2 }\times 11^{ 8 } }{ 3\times 7\times 11^{ 3 } }$
= 3^{(1 – 1)}× 7^{(2 – 1)}× 11^{(8 – 3)} (∵ $\cfrac { a^{ m } }{ a^{ n } }$ = a^{m – n})
= 3⁰ ×7¹ × 11⁵= 1 ×7 × 11⁵ (∵ a⁰ = 1)
= 7 × 11⁵

v) $\cfrac { 3^{ 7 } }{ 3^{ 4 }\times 3^{ 3 } }$
= $\cfrac { 3^{ 7 } }{ 3^{ (4+3) } }$ (∵ a^m × aⁿ = a^{m + n})
= $\cfrac { 3^{ 7 } }{ 3^{ 7 } }$
= 3^(7-7)= 3⁰= 1 (∵ a⁰ = 1)

vi) 2⁰ + 3⁰+ 4⁰
= 1 + 1 + 1 (∵ a⁰ = 1)
= 3

vii) 2⁰ × 3⁰× 4⁰
= 1 × 1 × 1 (∵ a⁰ = 1)
= 1

viii) (3⁰ + 2⁰) × 5⁰
= (1 + 1) × 1 (∵ a⁰ = 1)
= 2 × 1
= 2

ix) $\cfrac { 2^{ 8 }\times a^{ 5 } }{ 4^{ 3 }\times a^{ 3 } }$
= $\cfrac { 2^{ 8 }\times a^{ 5 } }{ (2^{ 2 })^{ 3 }\times a^{ 3 } }$
= $\cfrac { 2^{ 8 }\times a^{ 5 } }{ 2^{ (2\times 3) }\times a^{ 3 } }$ (∵ (a^m)ⁿ = a^mn)
= $\cfrac { 2^{ 8 }\times a^{ 5 } }{ 2^{ 6 }\times a^{ 3 } }$
= 2^(8-6)×a^(5-3) (∵ $\cfrac { a^{ m } }{ a^{ n } }$ = a^{m – n})
= 2² × a²= (2a)² (∵ (a^mx b^m = (ab)^m)

x) $\cfrac { a^{ 5 } }{ a^{ 3 } } \times a^{ 8 }$
= (a^{5 – 3}) × a⁸ (∵ $\cfrac { a^{ m } }{ a^{ n } }$ = a^{m – n})
= a² × a⁸= a²⁺⁸ (∵ a^m × aⁿ = a^{m + n})
= a¹⁰

xi) $\cfrac { 4^{ 5 }\times a^{ 8 }b^{ 3 } }{ 4^{ 5 }\times a^{ 5 }b^{ 2 } }$
= 4^{5 – 5} × a^{8 – 5} × b^{3 – 2} (∵ $\cfrac { a^{ m } }{ a^{ n } }$ = a^{m – n})
= 4⁰ × a³ × b
= 1 × a³ × b (∵ a⁰ = 1)
= a³ × b

xii) (2³ × 2)²
= (2^{3 + 1})² (∵ a^m × aⁿ = a^{m + n})
= (2⁴)²= 2^{4 × 2} (∵ (a^m)ⁿ = a^mn)
= 2⁸

3. Say true or false and justify your answer:

i) 10 × 10¹¹ = 100¹¹ii) 2³ > 5²iii) 2³ × 3² = 6⁵iv) 3⁰ = (1000)⁰

i) False
LHS = 10 × 10¹¹= 10^{1 + 11}(∵ a^m × aⁿ = a^{m + n})
= 10¹²RHS = 100¹¹= (10²)¹¹= 10²²(∵ (a^m)ⁿ = a^mn)
∴ LHS ≠ RHS
Hence, this statement is false.

ii) False
2³ = 2 × 2 × 2 = 8
5² = 5 × 5 = 25
∵ 8 < 25
∴ 2³ < 5²Hence, this statement is false.

iii) False
LHS = 2³ × 3²= 2 × 2 × 2 × 3 × 3
= 72
RHS = 6⁵= 6 × 6 × 6 × 6 × 6
= 7776
∴ LHS ≠ RHS
Hence, this statement is false.

iv) True
∵ Any number raised to the power zero equal to 1
∴ 3⁰ = (1000)⁰ = 1
Hence, this statement is true.

4. Express each of the following as a product of prime factors only in exponential form:

i) 108 × 192
ii) 270
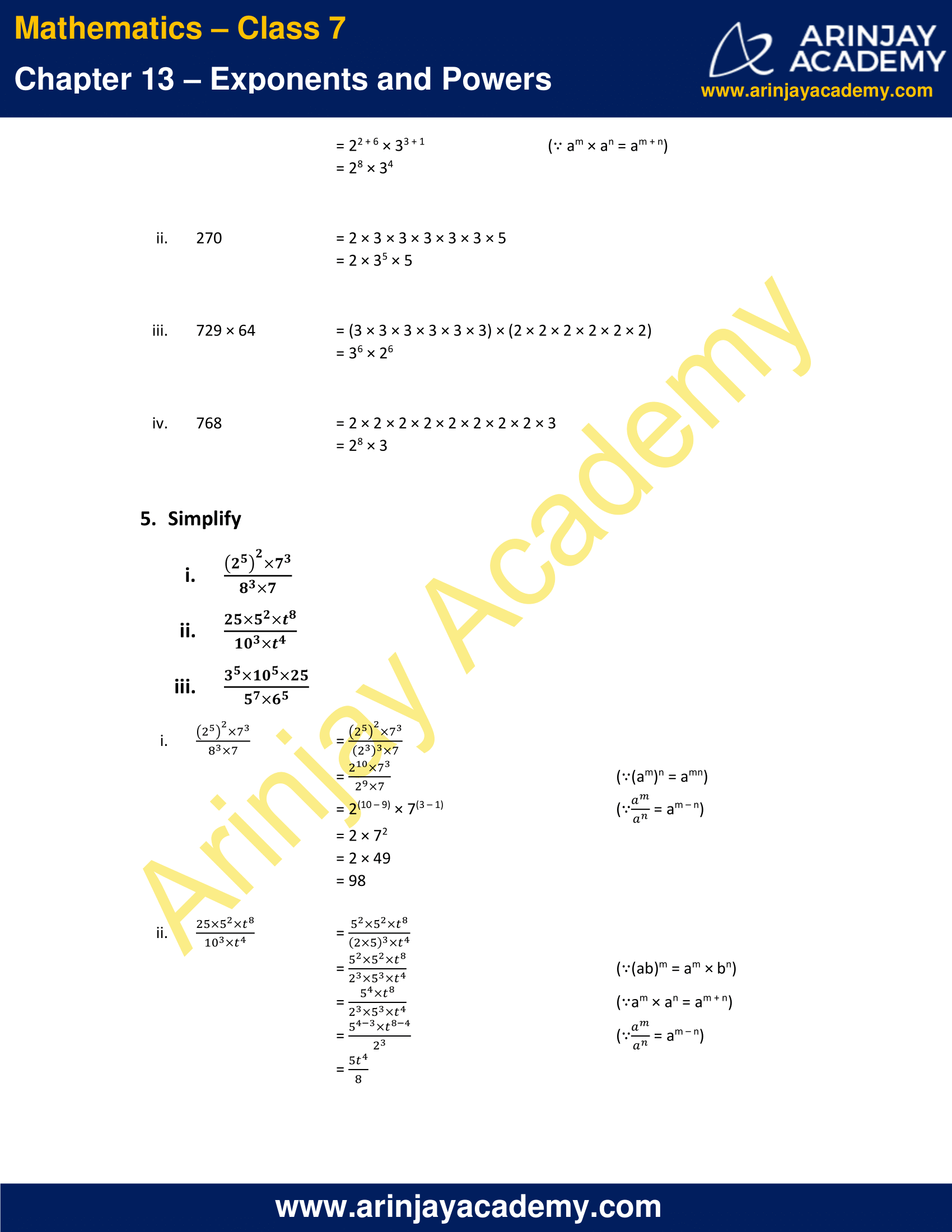
iii) 729 × 64
iv) 768

i) 108 × 192 = (2 × 2 × 3 × 3 × 3) × (2 × 2 × 2 × 2 × 2 × 2 × 3)
= (2² × 3³) × (2⁶ × 3)
= 2^{2 + 6} × 3^{3 + 1}(∵ a^m × aⁿ = a^{m + n})
= 2⁸ × 3⁴

ii) 270 = 2 × 3 × 3 × 3 × 3 × 3 × 5
= 2 × 3⁵ × 5

iii) 729 × 64 = (3 × 3 × 3 × 3 × 3 × 3) × (2 × 2 × 2 × 2 × 2 × 2)
= 3⁶ × 2⁶

iv) 768 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3
= 2⁸ × 3

5. Simplify

i) $\cfrac { (2^{ 5 })^{ 2 }\times 7^{ 3 } }{ 8^{ 3 }\times 7 }$
ii) $\cfrac { 25\times 5^{ 2 }\times t^{ 8 } }{ 10^{ 3 }\times t^{ 4 } }$
iii) $\cfrac { 3^{ 5 }\times 10^{ 5 }\times 25 }{ 5^{ 7 }\times 6^{ 5 } }$

i) $\cfrac { (2^{ 5 })^{ 2 }\times 7^{ 3 } }{ 8^{ 3 }\times 7 }$
= $\cfrac { (2^{ 5 })^{ 2 }\times 7^{ 3 } }{ (2^{ 3 })^{ 3 }\times 7 }$
= $\cfrac { 2^{ 10 }\times 7^{ 3 } }{ 2^{ 9 }\times 7 }$ (∵ (a^m)ⁿ = a^mn)
= 2^{(10 – 9)} × 7^{(3 – 1)} (∵ $\cfrac { a^{ m } }{ a^{ n } }$ = a^{m – n})
= 2 × 7²= 2 × 49
= 98

ii) $\cfrac { 25\times 5^{ 2 }\times t^{ 8 } }{ 10^{ 3 }\times t^{ 4 } }$
= $\cfrac { 5^{ 2 }\times 5^{ 2 }\times t^{ 8 } }{ (2\times 5)^{ 3 }\times t^{ 4 } }$
= $\cfrac { 5^{ 2 }\times 5^{ 2 }\times t^{ 8 } }{ 2^{ 3 }\times 5^{ 3 }\times t^{ 4 } }$ (∵ (ab)^m = a^m × bⁿ)
= $\cfrac { 5^{ 4 }\times t^{ 8 } }{ 2^{ 3 }\times 5^{ 3 }\times t^{ 4 } }$ (∵ a^m × aⁿ = a^{m + n})
= $\cfrac { 5^{ (4-3) }\times t^{ (8-4) } }{ 2^{ 3 } }$ (∵ $\cfrac { a^{ m } }{ a^{ n } }$ = a^{m – n})
= $\cfrac { 5t^{ 4 } }{ 8 }$

iii) $\cfrac { 3^{ 5 }\times 10^{ 5 }\times 25 }{ 5^{ 7 }\times 6^{ 5 } }$
= $\cfrac { 3^{ 5 }\times (2\times 5)^{ 5 }\times 5^{ 2 } }{ 5^{ 7 }\times (2\times 3)^{ 5 } }$
= $\cfrac { 3^{ 5 }\times 2^{ 5 }\times 5^{ 5 }\times 5^{ 2 } }{ 2^{ 5 }\times 3^{ 5 }\times 5^{ 7 } }$ (∵ (ab)^m = a^m × bⁿ)
= $\cfrac { 2^{ 5 }\times 3^{ 5 }\times 5^{ (5+2) } }{ 2^{ 5 }\times 3^{ 5 }\times 5^{ 7 } }$ (∵ a^m × aⁿ = a^{m + n})
= $\cfrac { 2^{ 5 }\times 3^{ 5 }\times 5^{ 7 } }{ 2^{ 5 }\times 3^{ 5 }\times 5^{ 7 } }$
= $2^{ (5-5) }\times 3^{ (5-5) }\times 5^{ (7-7) }$
= $2^{ 0 }\times 3^{ 0 }\times 5^{ 0 }$
= 1 x 1 x 1
= 1 (∵ a⁰ = 1)

NCERT Solutions for Class 7 Maths Chapter 13 Exercise 13.3

1. Write the following numbers in the expanded forms:
279404, 3006194, 2806196, 120719, 20068

279404 = 2 × 100000 + 7 × 10000 + 9 × 1000 + 4 × 100 + 0 × 10 + 4
= 2 × 10⁵ + 7 × 10⁴ + 9 × 10³ + 4 × 10² + 0 × 10¹ + 4 × 10⁰
3006194 = 3 × 1000000 + 0 × 100000 + 0 × 10000 + 6 × 1000 + 1 × 100 + 9 × 10 + 4
= 3 × 10⁶ + 0 × 10⁵ + 0 × 10⁴ + 6 × 10³ + 1 × 10² + 9 × 10¹ + 4 × 10⁰
2806196 = 2 × 1000000 + 8 × 100000 + 0 × 10000 + 6 × 1000 + 1 × 100 + 9 × 10 + 6
= 2 × 10⁶ + 8 × 10⁵ + 0 × 10⁴ + 6 × 10³ + 1 × 10² + 9 × 10¹ + 6 × 10⁰
120719 = 1 × 100000 + 2 × 10000 + 0 × 1000 + 7 × 100 + 1 × 10 + 9
= 1 × 10⁵ + 2 × 10⁴ + 0 × 10³ + 7 × 10² + 1 × 10¹ + 9 × 10⁰
20068 = 2 × 10000 + 0 × 1000 + 0 × 100 + 6 × 10 + 8
= 2 × 10⁴ + 0 × 10³ + 0 × 10² + 6 × 10¹ + 8 × 10⁰

2. Find the number from each of the following expanded forms:

a) 8 × 10⁴ + 6 × 10³ + 0 × 10² + 4 × 10¹ + 5 × 10⁰b) 4 × 10⁵ + 5 × 10³ + 3 × 10² + 2 × 10⁰c) 3 × 10⁴ + 7 × 10² + 5 × 10⁰d) 9 × 10⁵ + 2 × 10² + 3 × 10¹

a) 8 × 10⁴ + 6 × 10³ + 0 × 10² + 4 × 10¹ + 5 × 10⁰= 8 × 10000 + 6 × 1000 + 0 × 100 + 4 × 10 + 5 × 1
= 80000 + 6000 + 0 + 40 + 5
= 86045

b) 4 × 10⁵ + 5 × 10³ + 3 × 10² + 2 × 10⁰= 4 × 100000 + 5 × 1000 + 3 × 100 + 2 × 1
= 400000 + 5000 + 300 + 2
= 405302

c) 3 × 10⁴ + 7 × 10² + 5 × 10⁰= 3 × 10000 + 7 × 100 + 5 × 1
= 30000 + 700 + 5
= 30705

d) 9 × 10⁵ + 2 × 10² + 3 × 10¹= 9 × 100000 + 2 × 100 + 3 × 10
= 900000 + 200 + 30
= 900230

3. Express the following numbers in standard form:

i) 5,00,00,000
ii) 70,00,000
iii) 3,18,65,00,000
iv) 3,90,878
v) 39087.8
vi) 3908.78

i) 5,00,00,000 = 5 × 1,00,00,000 = 5 × 10⁷ii) 70,00,000 = 7 × 10,00,000 = 7 × 10⁶iii) 3,18,65,00,000 = 3.1865 × 1,00,00,00,000 = 3.1865 × 10⁹iv) 3,90,878 = 3.90878 × 1,00,000 = 3.90878 × 10⁵v) 39087.8 = 3.90878 × 10,000 = 3.90878 × 10⁴vi) 3908.78 = 3.90878 × 1,000 = 3.90878 × 10³

4. Express the number appearing in the following statements in standard form.

a) The distance between Earth and Moon is 384,000,000 m.
b) Speed of light in vacuum is 300,000,000 m/s.
c) Diameter of the Earth is 1,27,56,000 m.
d) Diameter of the Sun is 1,400,000,000 m.
e) In a galaxy there are on an average 100,000,000,000 stars.
f) The universe is estimated to be about 12,000,000,000 years old.
g) The distance of the Sun from the centre of the Milky Way Galaxy is estimated to be 300,000,000,000,000,000,000 m.
h) 60,230,000,000,000,000,000,000 molecules are contained in a drop of water weighing 1.8 gm.
i) The earth has 1,353,000,000 cubic km of sea water.
j) The population of India was about 1,027,000,000 in March, 2001.

a) 384,000,000 m
= 3.84 × 100,000,000
= 3.84 × 10⁸ m

b) 300,000,000 m/s
= 3 × 100,000,000
= 3 × 10⁸ m/s

c) 1,27,56,000 m
= 1.2756 × 1,00,00,000
= 1.2756 × 10⁷ m

d) 1,400,000,000 m
= 1.4 × 1,000,000,000
= 1.4 × 10⁹ m

e) 100,000,000,000
= 1 × 100,000,000,000
= 1 × 10¹¹

f) 12,000,000,000 years
= 1.2 × 10,000,000,000
= 1.2 × 10¹⁰ years

g) 300,000,000,000,000,000,000 m
= 3 × 100,000,000,000,000,000,000
= 3 × 10²⁰ m

h) 60,230,000,000,000,000,000,000
= 6.023 × 10,000,000,000,000,000,000,000
= 6.023 × 10²²

i) 1,353,000,000 cubic km
= 1.353 × 1, 000,000,000
= 1.353 × 10⁹ cubic km

j) 1,027,000,000
= 1.027 × 1,000,000,000
= 1.027 × 10⁹

This Chapter contains the Exercises relating to the following topics , which are discussed in Chapter 13 – Exponents and Powers Class 7 NCERT book : –

13.1 INTRODUCTION
13.2 EXPONENTS
13.3 LAWS OF EXPONENTS
13.3.1 Multiplying Powers with the Same Base
13.3.2 Dividing Powers with the Same Base
13.3.3 Taking Power of a Power
13.3.4 Multiplying Powers with the Same Exponents
13.3.5 Dividing Powers with the Same Exponents
13.4 MISCELLANEOUS EXAMPLES USING THE LAWS OF EXPONENTS
13.5 DECIMAL NUMBER SYSTEM
13.6 EXPRESSING LARGE NUMBERS IN THE STANDARD FORM

Download NCERT Solutions for Class 7 Maths Chapter 13 – Exponents and Powers

NCERT Solutions for Class 7 Maths Chapter 13 – Exponents and Powers

NCERT Solutions for Class 7 Maths Chapter 13 Exercise 13.1

NCERT Solutions for Class 7 Maths Chapter 13 Exercise 13.2

NCERT Solutions for Class 7 Maths Chapter 13 Exercise 13.3

NCERT Solutions for Class 7 Maths Chapter 13 Exercise 13.1

NCERT Solutions for Class 7 Maths Chapter 13 Exercise 13.2

NCERT Solutions for Class 7 Maths Chapter 13 Exercise 13.3

NCERT Solutions for Class 7

CBSE Notes for Class 7

Worksheets for Class 7

Leave a Comment Cancel reply