Class 7 Maths NCERT Solutions Chapter 11 – Perimeter and Area comprises of the 4 Exercises
This Chapter contains the Exercises relating to the following topics , which are discussed in Chapter 11 – Perimeter and Area Class 7 NCERT book : –
- 11.1 INTRODUCTION
- 11.2 SQUARES AND RECTANGLES
- 11.2.1 Triangles as Parts of Rectangles
- 11.2.2 Generalising for other Congruent Parts of Rectangles
- 11.3 AREA OF A PARALLELOGRAM
- 11.4 AREA OF A TRIANGLE
- 11.5 CIRCLES
- 11.5.1 Circumference of a Circle
- 11.5.2 Area of Circle
- 11.6 CONVERSION OF UNITS
- 11.7 APPLICATIONS
NCERT Solutions for Class 7 Maths Chapter 11 Exercise 11.1



NCERT Solutions for Class 7 Maths Chapter 11 Exercise 11.2



NCERT Solutions for Class 7 Maths Chapter 11 Exercise 11.3







NCERT Solutions for Class 7 Maths Chapter 11 Exercise 11.4


NCERT Solutions for Class 7 Maths Chapter 11 Exercise 11.1
1. The length and the breadth of a rectangular piece of land are 500 m and 300 m respectively. Find
i. Its area
ii. The cost of the land, if 1 m2 of the land costs Rs. 10,000.
Solution:
i. Length = 500 m
Breadth = 300 m
Area of rectangular piece of land = length × breadth
= 500 × 300
= 150000 m2
ii. Cost of 1 m2 of land = Rs. 10,000
Cost of 150000 m2 of land = Rs. 10,000 × 150000
= Rs. 1500000000
2. Find the area of a square park whose perimeter is 320 m.
Solution:
Let the side of the square be s
Perimeter of the square = 320 m
4s = 320 m
s = 80 m
Area of the square = (side)2 = s2
= 802
= 6400 m2
3. Find the breadth of a rectangular plot of land, if its area is 440 m2 and the length is 22 m. Also find its perimeter.
Solution:
Let the breadth of the rectangle be b
Length of the rectangle = 22 m
Area of the rectangle = 440 m2
Length × Breadth = 440 m2
22 × b = 440
b = 20 m
Perimeter of rectangle = 2 × (Length + Breadth)
= 2 × (22 + 20)
= 2 × 42
= 84 m2
4. The perimeter of a rectangular sheet is 100 cm. If the length is 35 cm, find its breadth. Also find the area.
Solution:
Let the breadth of the rectangle be b
Length of the rectangle = 35 cm
Perimeter of the rectangle = 100 cm
2 × (Length + Breadth) = 100 cm
2 × (35 + b) = 100
35 + b = 50
b = 15 cm
Area of the rectangle = Length × Breadth
= 35 × 15
= 525 cm2
5. The area of a square park is the same as of a rectangular park. If the side of the square park is 60 m and the length of the rectangular park is 90 m, find the breadth of the rectangular park.
Solution:
Let the breadth of the rectangular park be b
Length of the rectangle = 90 m
Side of the square = 60 m
Area of square = (side)2 = 602 = 3600 m2
Area of rectangle = Length × Breadth = 90 × b
According to the question,
Area of square = Area of rectangle
3600 = 90 × b
b = 3600/90 = 40 m
6. A wire is in the shape of a rectangle. Its length is 40 cm and breadth is 22 cm. If the same wire is rebent in the shape of a square, what will be the measure of each side. Also find which shape encloses more area?
Solution:
Length of rectangle = 40 cm
Breadth of rectangle = 22 cm
Let the side of the square be s
Perimeter of rectangle = 2 × (Length + Breadth) = 2 × (40 + 22) = 2 × (62) = 124 cm
Perimeter of square = 4 × (side) = 4s
Since the same wire is rebent from a rectangle to a square
Therefore, perimeter of square = perimeter of rectangle = length of the wire
4s = 124
s = 31 cm
Area of rectangle = Length × Breadth = 40 × 22 = 880 cm2
Area of square = (Side)2 = 312 = 961 cm2
Hence, the side of the square is 31 cm and square encloses more area than the rectangle.
7. The perimeter of a rectangle is 130 cm. If the breadth of the rectangle is 30 cm, find its length. Also find the area of the rectangle.
Solution:
Let the length of rectangle be l
Breadth of rectangle = 30 cm
Perimeter of rectangle = 2 × (Length + Breadth) = 130 cm
2 × (l + 30) = 130
l + 30 = 65
l = 35 cm
Area of the rectangle = Length × Breadth = 35 × 30 = 1050 cm2
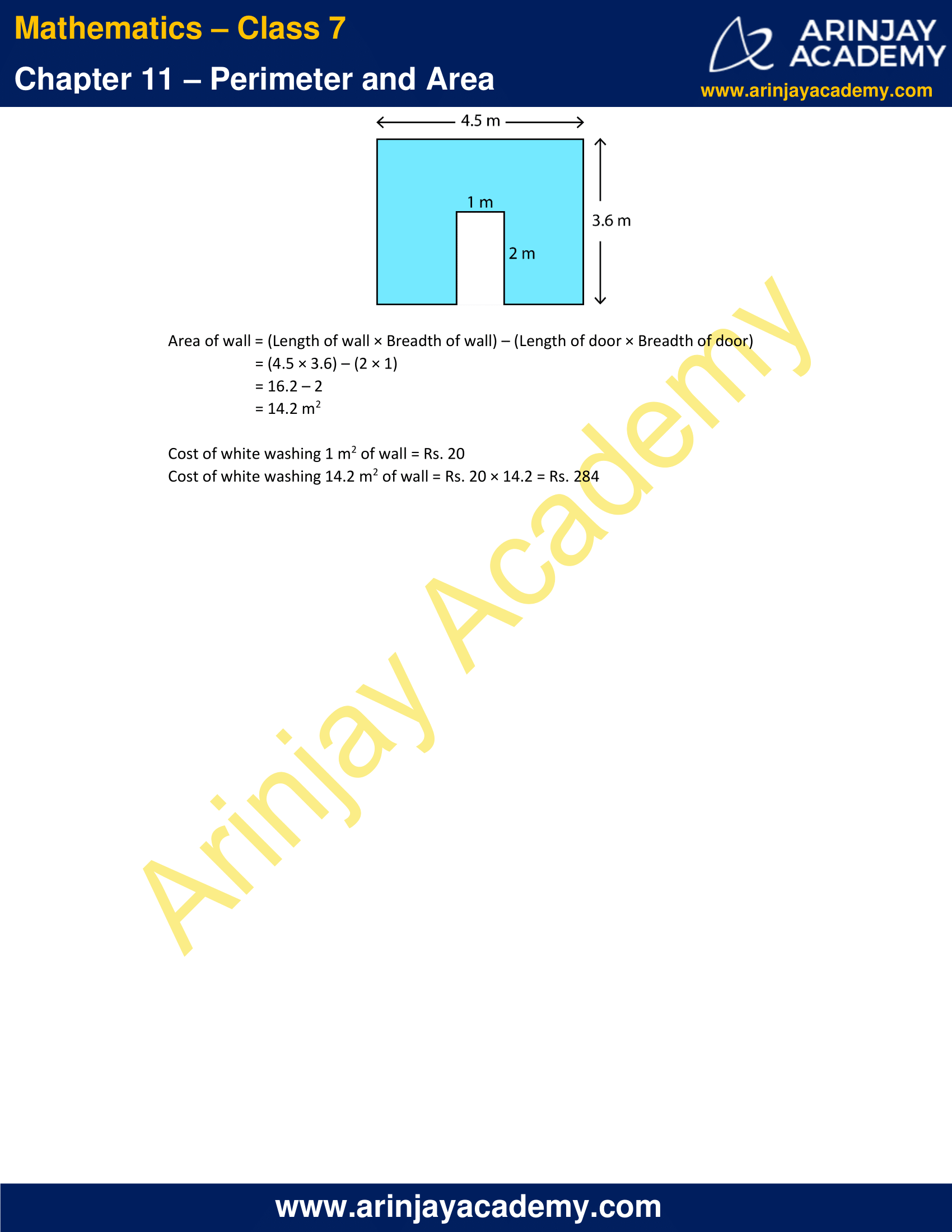
8. A door of length 2 m and breadth 1m is fitted in a wall. The length of the wall is 4.5 m and the breadth is 3.6 m. Find the cost of white washing the wall, if the rate of white washing the wall is Rs. 20 per m2.
Solution:
Length of door = 2 m
Breadth of door = 1 m
Length of wall = 4.5 m
Breadth of wall = 3.6 m
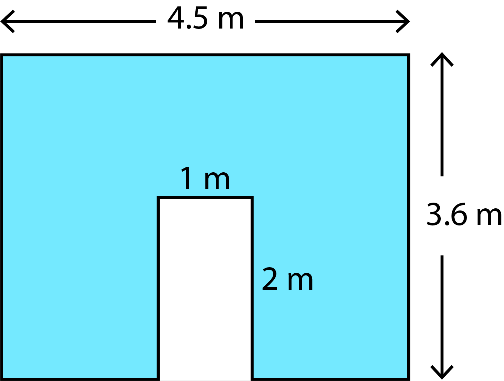
Area of wall = (Length of wall × Breadth of wall) – (Length of door × Breadth of door)
= (4.5 × 3.6) – (2 × 1)
= 16.2 – 2
= 14.2 m2
Cost of white washing 1 m2 of wall = Rs. 20
Cost of white washing 14.2 m2 of wall = Rs. 20 × 14.2 = Rs. 284
NCERT Solutions for Class 7 Maths Chapter 11 Exercise 11.2
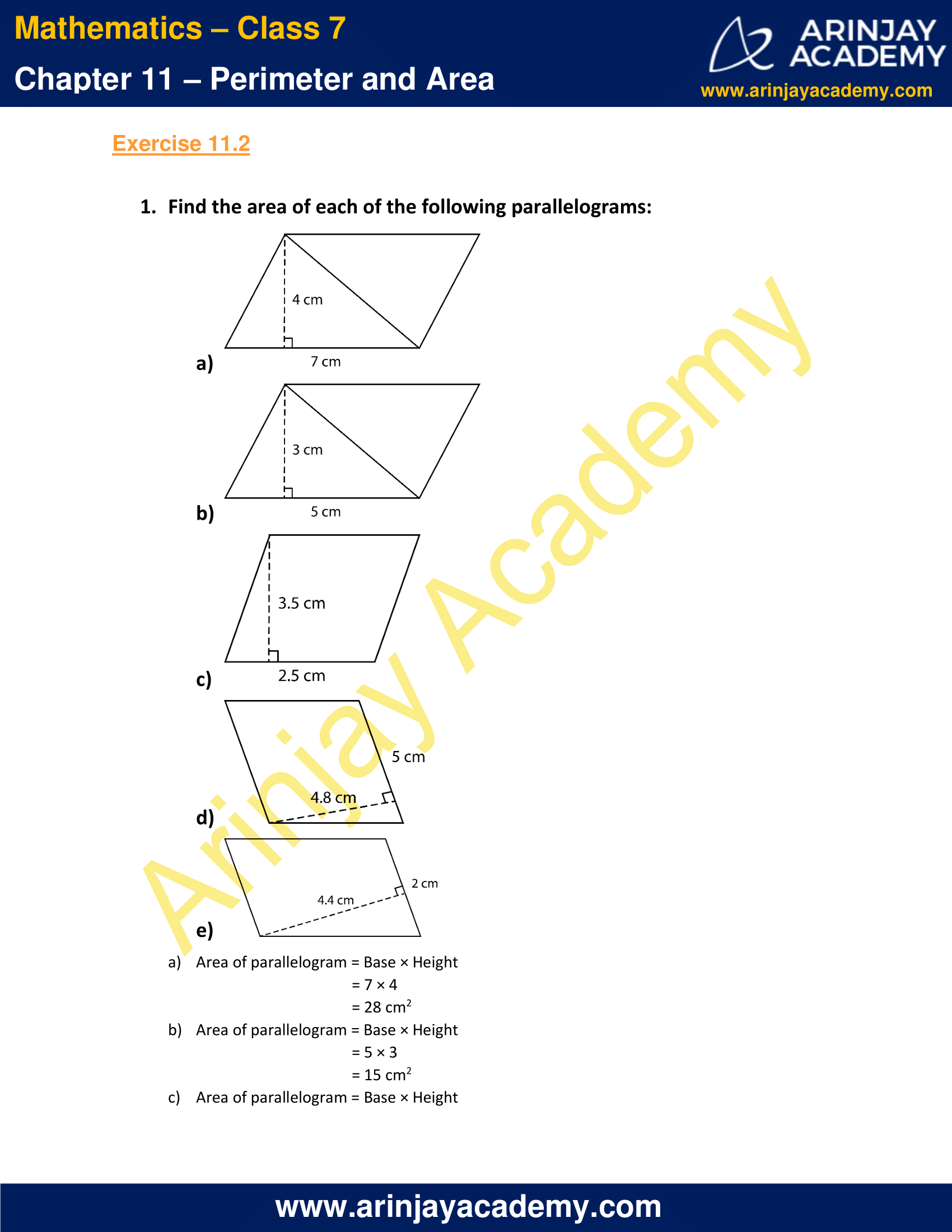
1. Find the area of each of the following parallelograms:
a)
b)
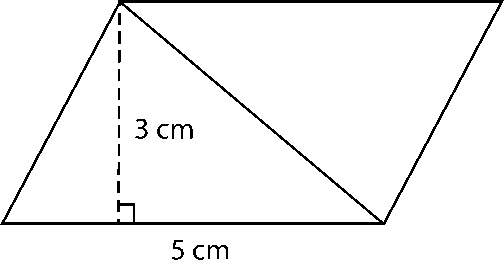
c)
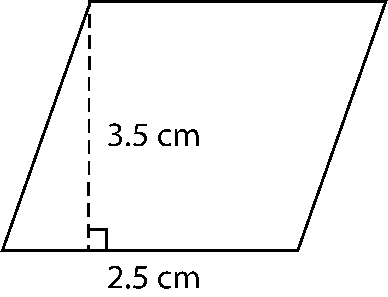
d)
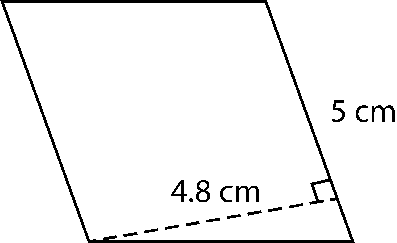
e)
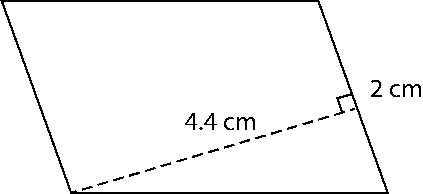
Solution:
a) Area of parallelogram = Base × Height
= 7 × 4
= 28 cm2
b) Area of parallelogram = Base × Height
= 5 × 3
= 15 cm2
c) Area of parallelogram = Base × Height
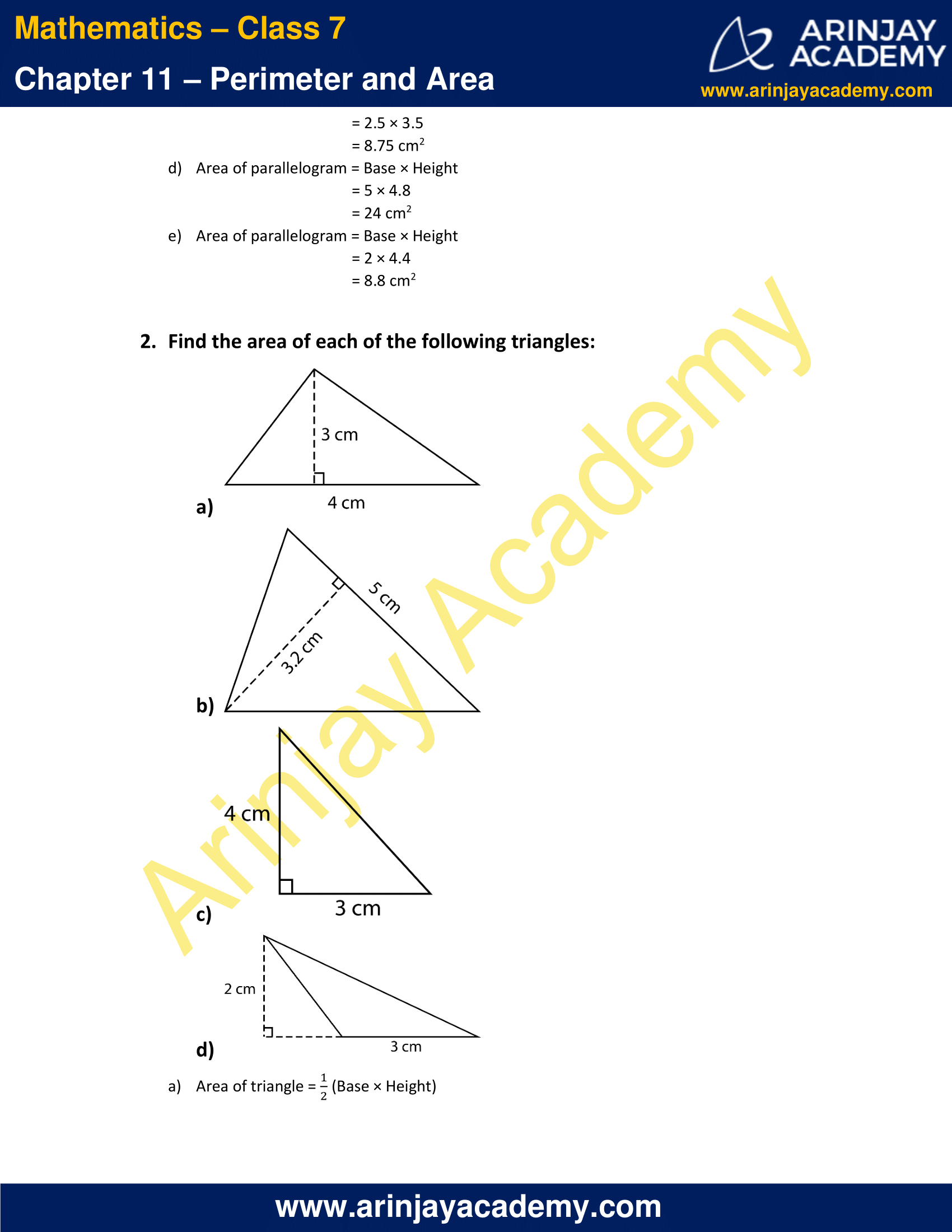
= 2.5 × 3.5
= 8.75 cm2
d) Area of parallelogram = Base × Height
= 5 × 4.8
= 24 cm2
e) Area of parallelogram = Base × Height
= 2 × 4.4
= 8.8 cm2
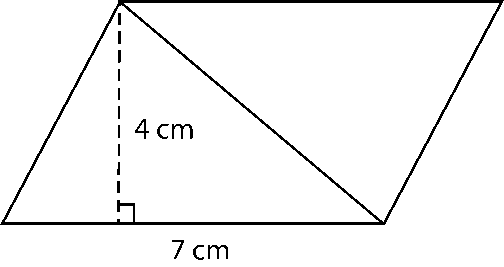
2. Find the area of each of the following triangles:
a)
b)
c)
d)
Solution:
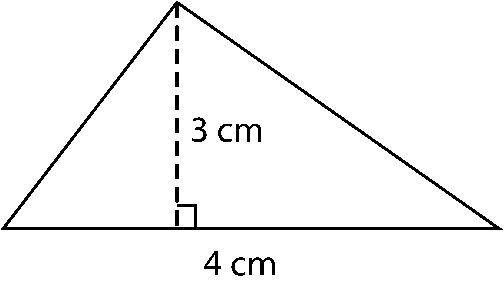
a) Area of triangle = 1/2 (Base × Height)
= 1/2 × 4 × 3
= 6 cm2
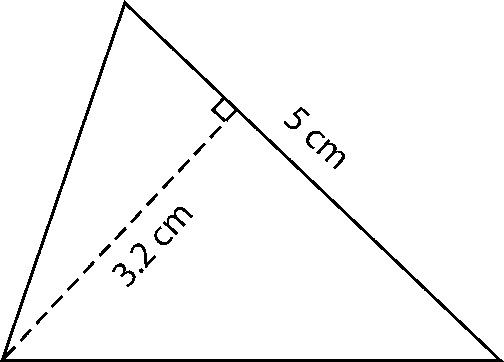
b) Area of triangle = 1/2 (Base × Height)
= 1/2 × 5 × 3.2
= 8 cm2
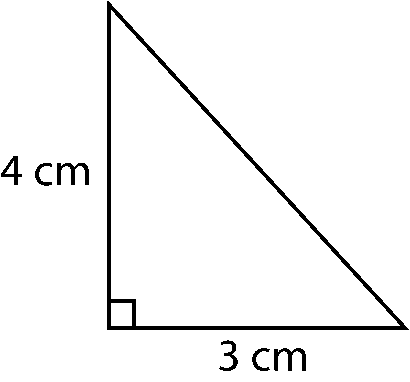
c) Area of triangle = 1/2 (Base × Height)
= 1/2 × 3 × 4
= 6 cm2
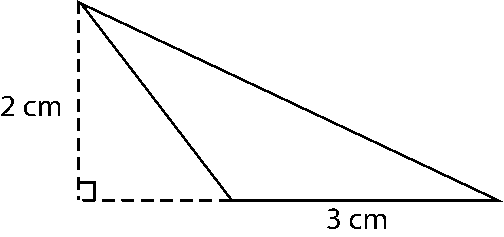
d) Area of triangle = 1/2 (Base × Height)
= 1/2 × 3 × 2
= 3 cm2
3. Find the missing values:
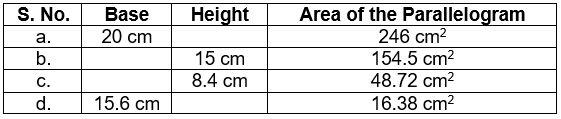
Solution:
a) Area of parallelogram = Base × Height
20 × Height = 246
Height = (246/20) cm = 12.3 cm
b) Area of parallelogram = Base × Height
Base × 15 = 154.5
Base = (154.5/15) cm = 10.3 cm
c) Area of parallelogram = Base × Height
Base × 8.4 = 48.72
Base = (48.72/8.4) cm = 5.8 cm
d) Area of parallelogram = Base × Height
15.6 × Height = 16.38
Height = (16.38/15.6) cm = 1.05 cm
4. Find the missing values:

Solution:
a) Area of triangle = 1/2 (Base × Height)
87 = 1/2 × 15 × Height
Height = (87 x 2)/15 = 11.6 cm
b) Area of triangle = 1/2 (Base × Height)
1256 = 1/2 × Base × 31.4
Base = (1256 x 2)/31.4 = 80 mm
c) Area of triangle = 1/2 (Base × Height)
170.5 = 1/2 × 22 × Height
Height = (70.5 x 2)/22 = 15.5 cm
5. PQRS is a parallelogram. QM is the height from Q to SR and QN is the height from Q to PS. If SR = 12 cm and QM = 7.6 cm. Find:
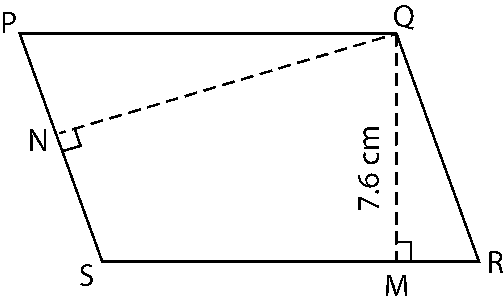
a) The area of the parallelogram PQRS
b) QN, if PS = 8 cm
Solution:
a) Area of parallelogram = Base × Height = SR × QM
= 12 × 7.6
= 91.2 cm2
b) Area of parallelogram = Base × Height = PS × QN
91.2 = 8 × QN
QN = 91.2/8 = 11.4 cm
6. DL and BM are the heights on sides AB and AD respectively of parallelogram ABCD. If the area of the parallelogram is 1470 cm2, AB = 35 cm and AD = 49 cm, find the length of BM and DL.
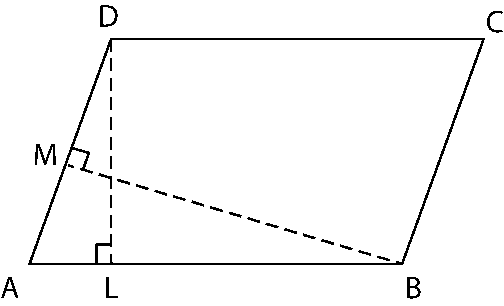
Solution:
Area of ABCD = 1470 cm2
Area of parallelogram = Base × Height = AB × DL = AD × BM
AB × DL = 1470 cm2
35 × DL = 1470
DL = 1470/35 = 42 cm
AD × BM = 1470 cm2
49 × BM = 1470
BM = 1470/49 = 30 cm
7. ∆ABC is right angled at A. AD is perpendicular to BC. If AB = 5 cm, BC = 13 cm and AC = 12 cm, Find the area of ∆ABC. Also find the length of AD.
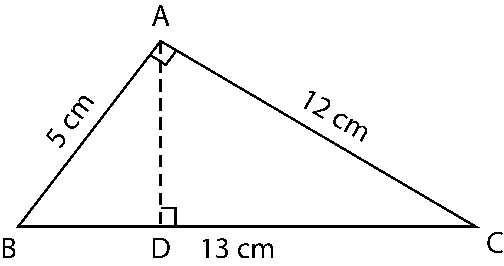
Solution:
Area of triangle = 1/2 × Base × Height = 1/2 × AB × AC
= 1/2 × 5 × 12
= 30 cm2
Area of triangle = 1/2 × Base × Height = 1/2 × BC × AD
1/2 × 13 × AD = 30
AD = (30 × 2)/13
AD = 60/13 cm
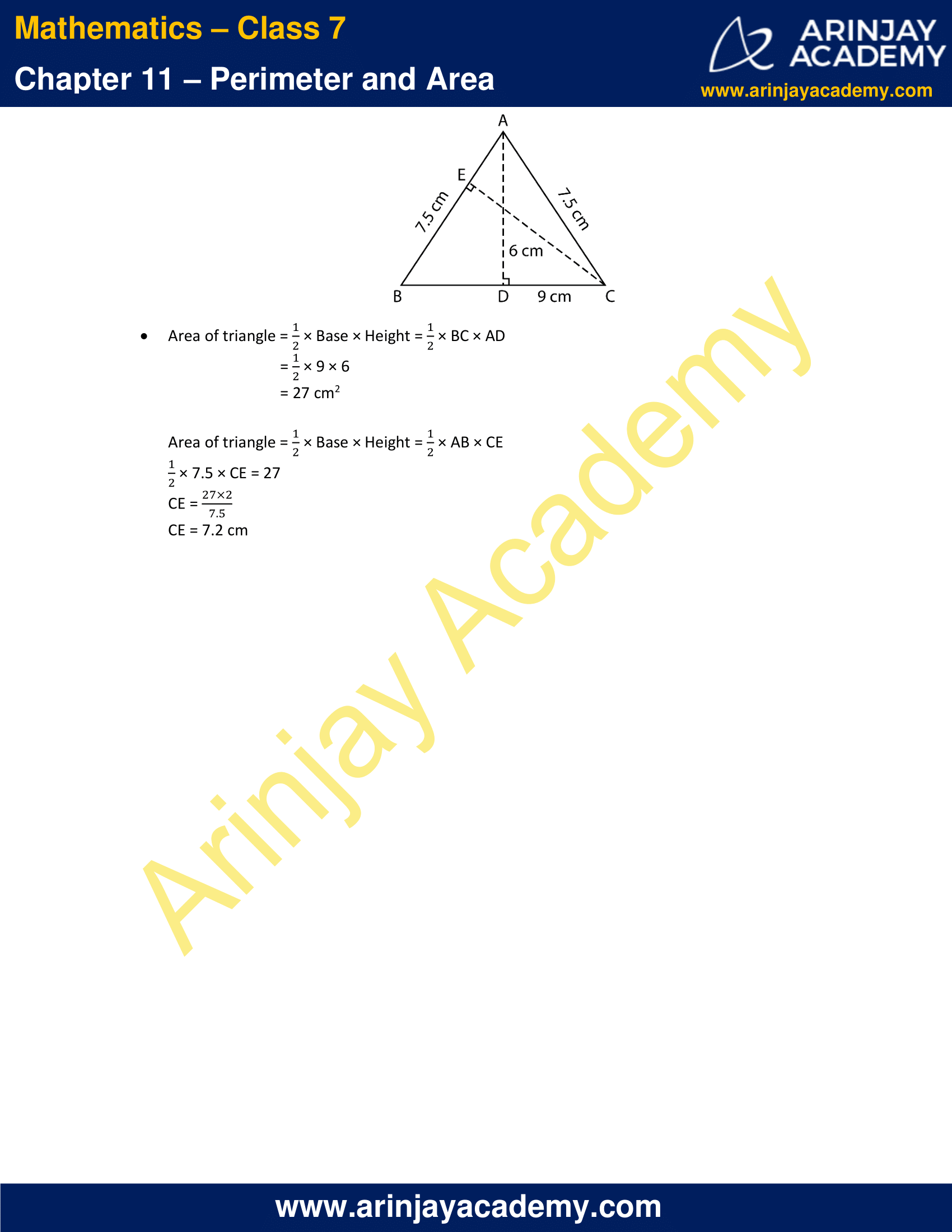
8. ∆ABC is isosceles with AB = AC = 7.5 cm and BC = 9 cm. The height AD from A to BC, is 6 cm. Find the area of ∆ABC. What will be the height from C to AB i.e., CE?
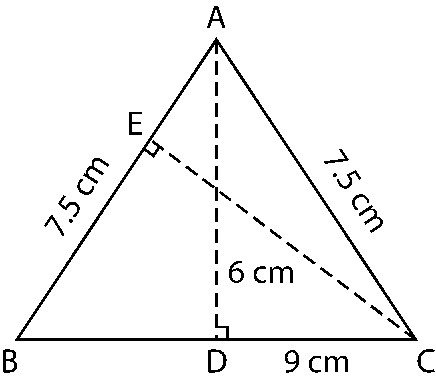
Solution:
Area of triangle = 1/2 × Base × Height = 1/2 × BC × AD
= 1/2 × 9 × 6
= 27 cm2
Area of triangle = 1/2 × Base × Height = 1/2 × AB × CE
1/2 × 7.5 × CE = 27
CE = (27 x 2)/7.5
CE = 7.2 cm
NCERT Solutions for Class 7 Maths Chapter 11 Exercise 11.3
1. Find the circumference of the circles with the following radius: (Take π = 22/7)
a) 14 cm
b) 28 mm
c) 21 cm
Solution:
a) Circumference of circle = 2πr
= 2 × (22/7) × 14
= 88 cm
b) Circumference of circle = 2πr
= 2 × (22/7) × 28
= 176 mm
c) Circumference of circle = 2πr
= 2 × 22/7 × 21
= 132 cm
2. Find the area of each of the following circles, given that:
a) Radius = 14 mm
b) Diameter = 49 m
c) Radius = 5 cm
a) Area of circle = πr2 = 22/7 × 142 = 616 mm2
b) Radius(r) = (Diameter/2) = (49/2) m
Area of circle = πr2 = (22/7) x (49/2)² = 1886.5 m2
c) Area of circle = πr2 = 22/7 × 52 = 550/7 cm2
3. If the circumference of a circular sheet is 154 m, find its radius. Also find the area of the sheet. (Take π = 22/7)
Solution:
Let the radius of the circle be r
Circumference = 2πr
2 × (22/7) × r = 154
r = (154 x 7)/(2 x 22) = 49/2 = 24.5 m
Area of circle = πr2 = 22/7 x (49/2)² = (22 x 49 x 49)(7 x 2 x 2) = 1886.5 m2
4. A gardener wants to fence a circular garden of diameter 21m. Find the length of the rope he needs to purchase, if he makes 2 rounds of fence. Also find the cost of the rope, if it costs Rs. 4 per meter. (Take π = 22/7)
Solution:
Radius of circular garden(r) = (Diameter/2) = 21/2 m
Circumference of the circular garden = 2πr = 2 × (22/7) × (21/2) = 66 m
Since the gardener makes 2 rounds of fence
Length of rope required = 2 × Circumference = 2 × 66 m = 132 m
Cost of 1 m of rope = Rs. 4
Cost of 132 m of rope = Rs. 4 × 132 = Rs. 528
5. From a circular sheet of radius 4 cm, a circle of radius 3 cm is removed. Find the area of the remaining sheet. (Take π = 3.14)

Solution:
Radius of circular sheet (R) = 4 cm
Radius of removed circle (r) = 3 cm
Area of remaining portion = Area of sheet – Area of removed circle
= πR2 – πr2
= 3.14 × 42 – 3.14 × 32
= 3.14 × (16 – 9)
= 3.14 × 7
= 21.98 cm2
6. Saima wants to put a lace on the edge of a circular table cover of diameter 1.5 m. Find the length of the lace required and also find its cost if one meter of the lace costs Rs. 15. (Take π = 3.14)
Solution:
Radius of table (r) = (Diameter/2) = (1.5/2) = 0.75 m
Circumference of table = 2πr = 2 × 3.14 × 0.75 = 4.71 m
Length of lace required = Circumference of the table = 4.71 m
Cost of 1 m of lace = Rs. 15
Cost of 4.71 m of lace = Rs. 15 × 4.71 = Rs. 70.65
7. Find the perimeter of the adjoining figure, which is a semicircle including its diameter.
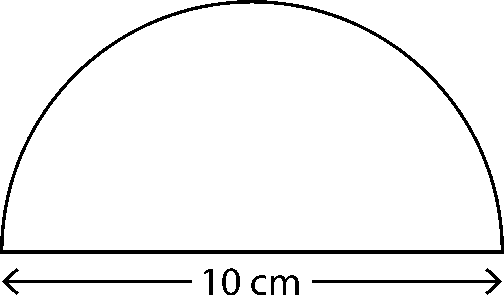
Solution:
Diameter of the semicircle (d) = 10 cm
Radius of the semicircle (r) = (Diameter/2) = 10/2 = 5 cm
Length of the curved part of semicircle = 1/2 × Circumference of circle = 1/2 × 2πr = πr
Circumference of the given semicircle = Length of curved part + diameter
= πr + d
= 3.14 × 5 + 10
= 15.7 + 10
= 25.7 cm
8. Find the cost of polishing a circular table-top of diameter 1.6 m, if the rate of polishing is Rs. 15/m2. (Take π = 3.14)
Solution:
Radius of table (r) = (Diameter/2) = (1.6/2) = 0.8 m
Area of table = πr2 = 3.14 × (0.8)2 = 3.14 × 0.64 = 2.0096 m2
Cost of polishing 1 m2 of table-top = Rs. 15
Cost of 2.0096 m of lace = Rs. 15 × 2.0096 = Rs. 30.144
9. Shazli took a wire of length 44 cm and bent it into the shape of a circle. Find the radius of that circle. Also find its area. If the same wire is bent into the shape of a square, what will be the length of each of its sides? Which figure encloses more area, the circle or the square? (Take π = 22/7)
Solution:
Let the radius of the wire be r
Length of the wire = Circumference of the circle = 2πr
2 × (22/7) × r = 44
r = (44 x 7)(22 x 2) = 7 cm
Area enclosed by circle = πr2 = 22/7 × 72 = 154 cm2
Let the length of the side of the square be s
Perimeter of square = 4s
Since the same wire is rebent from a circle to square
Perimeter of square = Length of the wire
4s = 44
s = 11 cm
Area enclosed by square = s2 = 112 = 121 cm2
Therefore, the circle encloses more area.
10. From a circular card sheet of radius 14 cm, two circles of radius 3.5 cm and a rectangle of length 3 cm and breadth 1cm are removed. (as shown in the adjoining figure). Find the area of the remaining sheet. (Take π = 22/7)

Solution:
Radius of circular card sheet (R) = 14 cm
Radius of removed circles (r) = 3.5 cm
Length of removed rectangle (l) = 3 cm
Breadth of removed rectangle (b) = 1 cm
Area of card sheet = πR2 = 22/7 × 142 = 616 cm2
Area of removed portion = Area of 2 removed circles + Area of removed rectangle
= 2 × (πr2) + (l × b)
= 2 × 22/7 × 3.52) + (3 × 1)
= 77 + 3
= 80 cm2
Remaining area = Area of card sheet – Area of removed portion
= 616 – 80
= 536 cm2
11. A circle of radius 2 cm is cut out from a square piece of an aluminium sheet of side 6 cm. What is the area of the left-over aluminium sheet? (Take π = 3.14)
Solution:
Radius of removed circle (r) = 2 cm
Side of the square sheet (s) = 6 cm
Area of left-over sheet = Area of square – Area of removed circle
= s2 – πr2
= 62 – 3.14 × 22
= 36 – 12.56
= 23.44 cm2
12. The circumference of a circle is 31.4 cm. Find the radius and the area of the circle? (Take π = 3.14)
Solution:
Let the radius of the circle be r
Circumference = 2πr
2 × 3.14 × r = 31.4
r = 31.4/(2 x 3.14) = 10/2 = 5 cm
Area of circle = πr2 = 3.14 × 52 = 3.14 × 25 = 78.5 cm2
13. A circular flower bed is surrounded by a path 4 m wide. The diameter of the flower bed is 66 m. What is the area of this path? (π = 3.14)
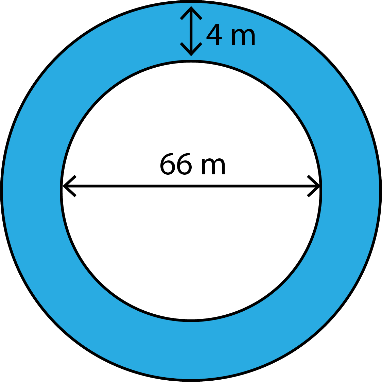
Radius of the flower bed (r) = (Diameter/2) = 66/2 =33 m
Radius of the surrounding path (R) = r + 4 = 33 + 4 = 37 m
Area of the path = Area of outer circle – Area of flower bed
= πR2 – πr2
= 3.14 × 372 – 3.14 × 332
= 3.14 × (372 – 332)
= 3.14 × (1369 – 1089)
= 3.14 × 280
= 879.2 m2
14. A circular flower garden has an area of 314 m2. A sprinkler at the centre of the garden can cover an area that has a radius of 12 m. Will the sprinkler water the entire garden? (Take π = 3.14)
Solution:
Area of garden = 314 m2
Radius of area covered by sprinkler (r) = 12 m
Area of garden covered by the sprinkler = πr2 = 3.14 × 122 = 452.16 m2
Since the area covered by the sprinkler is greater than the area of the garden
Hence, the sprinkler will water the entire garden.
15. Find the circumference of the inner and the outer circles, shown in the adjoining figure? (Take π = 3.14)
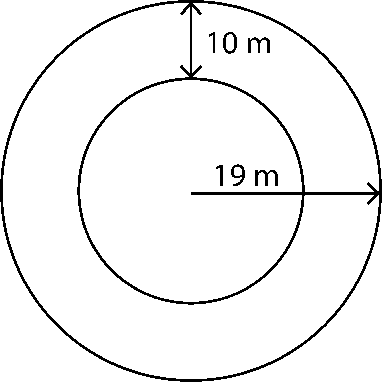
Solution:
Radius of outer circle (R) = 19 cm
Radius of inner circle (r) = 19 – 10 = 9 cm
Circumference of inner circle = 2πr = 2 × 3.14 × 9 = 56.52 cm
Circumference of outer circle = 2πR = 2 × 3.14 × 19 = 119.32 cm
16. How many times a wheel of radius 28 cm must rotate to go 352 m? (Take π = 22/7)
Solution:
Radius of wheel (r) = 28 cm
Circumference of the wheel = 2πr = 2 × (22/7) × 28 = 176 cm = 1.76 m
Distance travelled in 1 revolution = Circumference = 1.76 m
Revolution required to travel 1.76 m = 1
Revolution required to travel 1 m = (1/1.76)
Revolution required to travel 352 m = (352/1.76) = 200
17. The minute hand of a circular clock is 15 cm long. How far does the tip of the minute hand move in 1 hour. (Take π = 3.14)
Solution:
Length of the minute hand (r) = 15 cm
Circumference of circle traversed by the tip of minute hand = 2πr = 2 × 3.14 × 15 = 94.2 cm
In 1 hour, the minute hand completes a full circle
∴ Distance travelled by the tip of minute hand = Circumference = 94.2 cm
NCERT Solutions for Class 7 Maths Chapter 11 Exercise 11.4
1. A garden is 90 m long and 75 m broad. A path 5 m wide is to be built outside and around it. Find the area of the path. Also find the area of the garden in hectare.
Solution:
The dimensions of the garden and path are shown in the figure
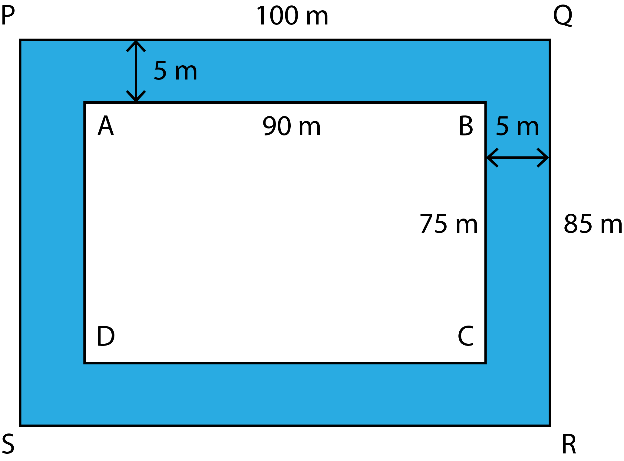
Area of the path = Area of PQRS – Area of ABCD
= 100 × 85 – 90 × 75
= 8500 – 6750
= 1750 m2
Area of garden = 90 × 75 = 6750 m2
= 0.675 hectare (1 hectare = 10000 m2)
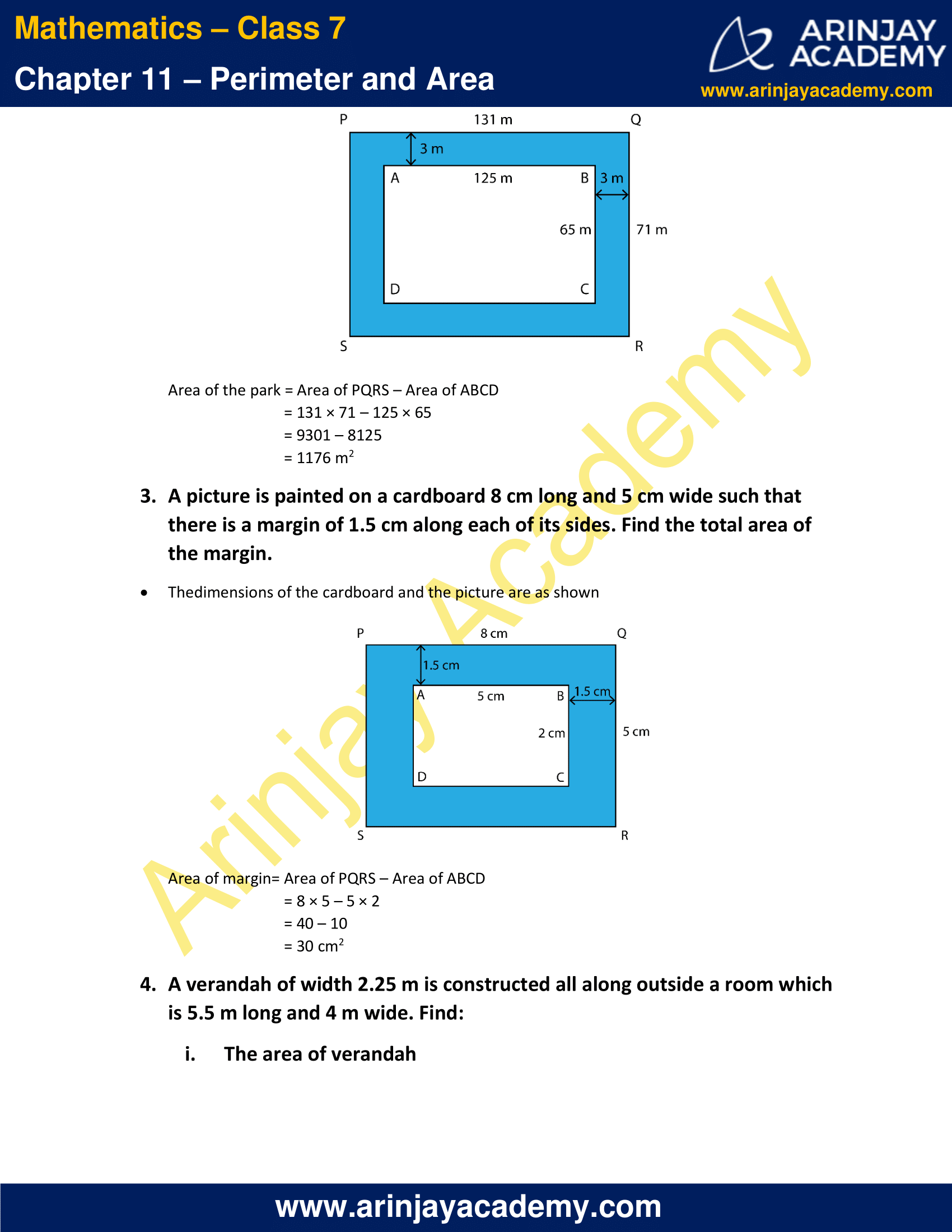
2. A 3 m wide path runs outside and around a rectangular park of length 125 m and breadth 65 m. Find the area of the path.
Solution:
The dimensions of the rectangular park and the path are shown in the figure
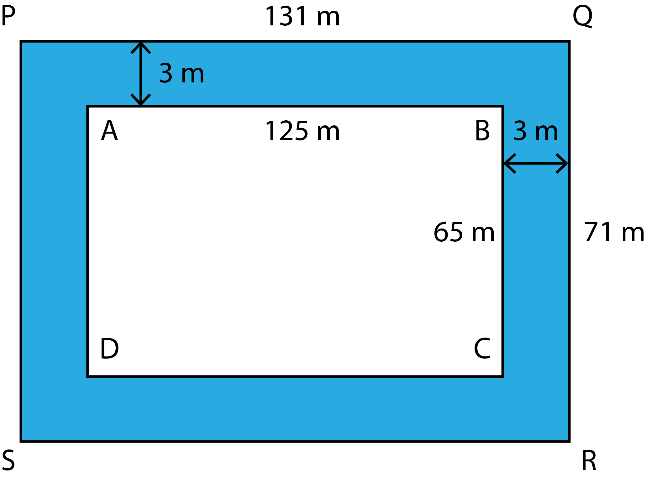
Area of the park = Area of PQRS – Area of ABCD
= 131 × 71 – 125 × 65
= 9301 – 8125
= 1176 m2
3. A picture is painted on a cardboard 8 cm long and 5 cm wide such that there is a margin of 1.5 cm along each of its sides. Find the total area of the margin.
Solution:
The dimensions of the cardboard and the picture are as shown
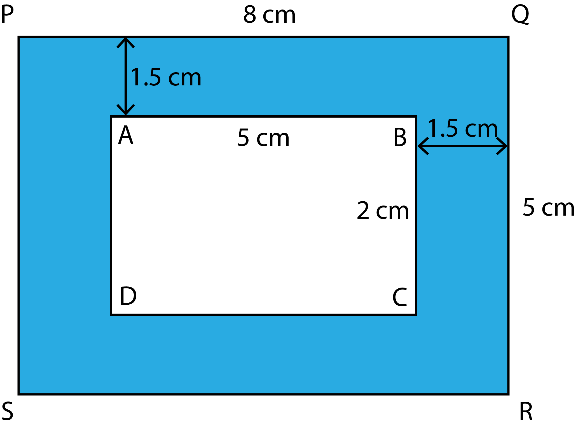
Area of margin = Area of PQRS – Area of ABCD
= 8 × 5 – 5 × 2
= 40 – 10
= 30 cm2
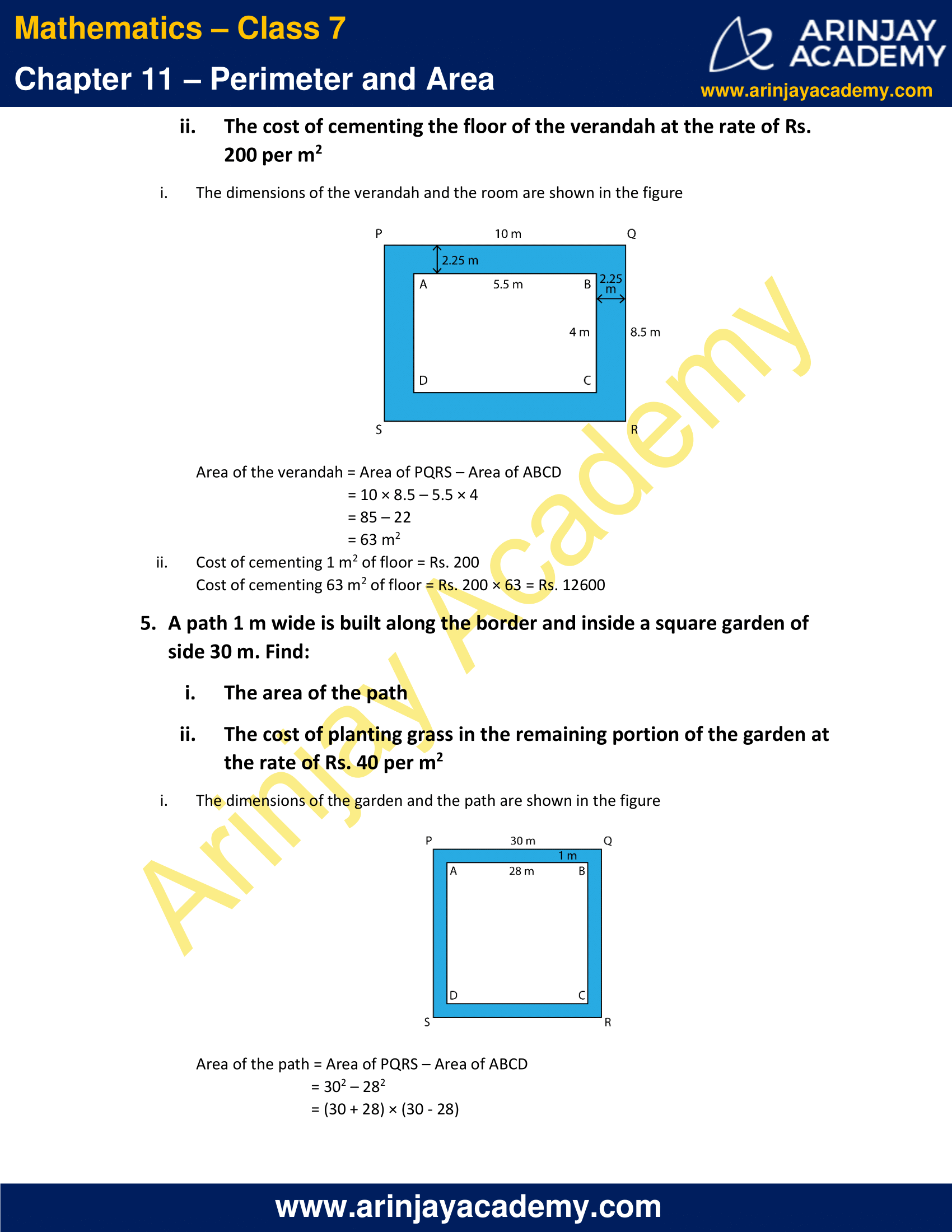
4. A verandah of width 2.25 m is constructed all along outside a room which is 5.5 m long and 4 m wide. Find:
i. The area of verandah
ii. The cost of cementing the floor of the verandah at the rate of Rs. 200 per m2
Solution:
i. The dimensions of the verandah and the room are shown in the figure
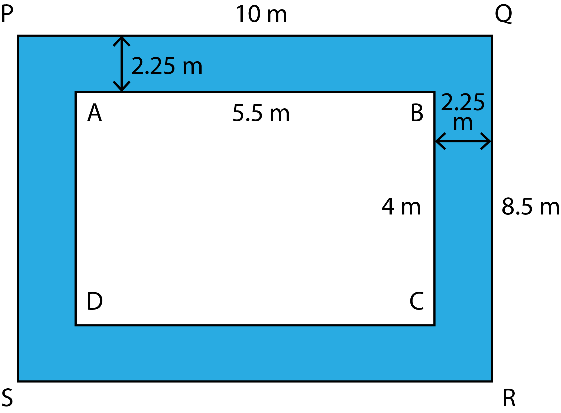
Area of the verandah = Area of PQRS – Area of ABCD
= 10 × 8.5 – 5.5 × 4
= 85 – 22
= 63 m2
ii. Cost of cementing 1 m2 of floor = Rs. 200
Cost of cementing 63 m2 of floor = Rs. 200 × 63 = Rs. 12600
5. A path 1 m wide is built along the border and inside a square garden of side 30 m. Find:
i. The area of the path
ii. The cost of planting grass in the remaining portion of the garden at the rate of Rs. 40 per m2
Solution:
i. The dimensions of the garden and the path are shown in the figure

Area of the path = Area of PQRS – Area of ABCD
= 302 – 282
= (30 + 28) × (30 – 28)
= 58 × 2
= 116 m2
ii. Area of remaining portion of the garden = 282 = 784 m2
Cost of planting grass in 1 m2 of land = Rs. 40
Cost of planting grass in 784 m2 of land = Rs. 40 × 784 = Rs. 31,360
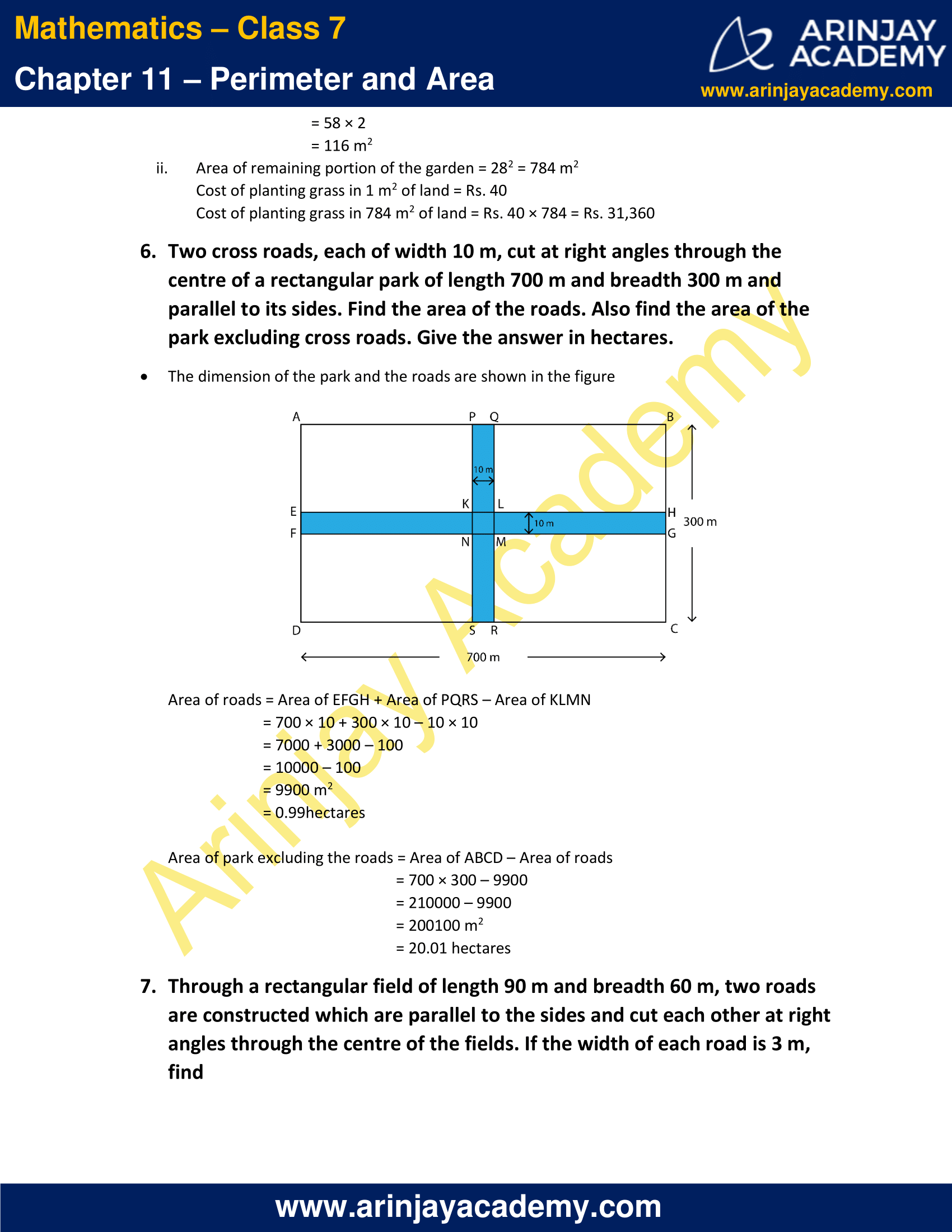
6. Two cross roads, each of width 10 m, cut at right angles through the centre of a rectangular park of length 700 m and breadth 300 m and parallel to its sides. Find the area of the roads. Also find the area of the park excluding cross roads. Give the answer in hectares.
Solution:
i. The dimension of the park and the roads are shown in the figure
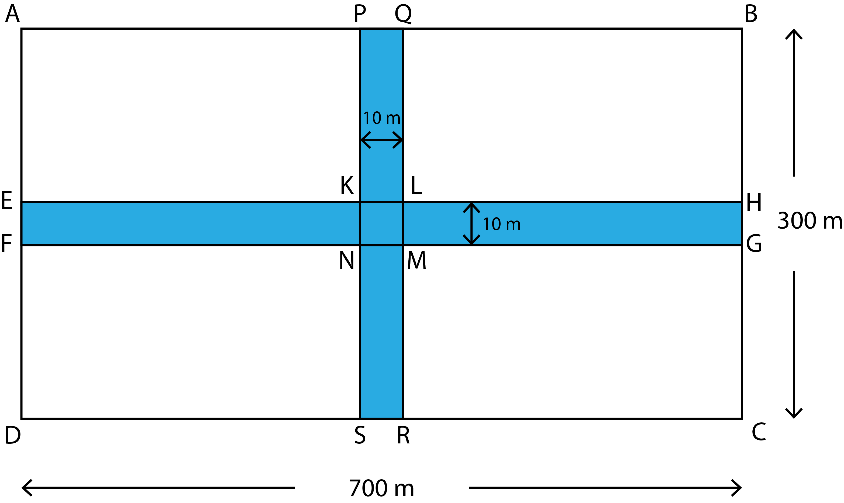
Area of roads = Area of EFGH + Area of PQRS – Area of KLMN
= 700 × 10 + 300 × 10 – 10 × 10
= 7000 + 3000 – 100
= 10000 – 100
= 9900 m2
= 0.99 hectares
Area of park excluding the roads = Area of ABCD – Area of roads
= 700 × 300 – 9900
= 210000 – 9900
= 200100 m2
= 20.01 hectares
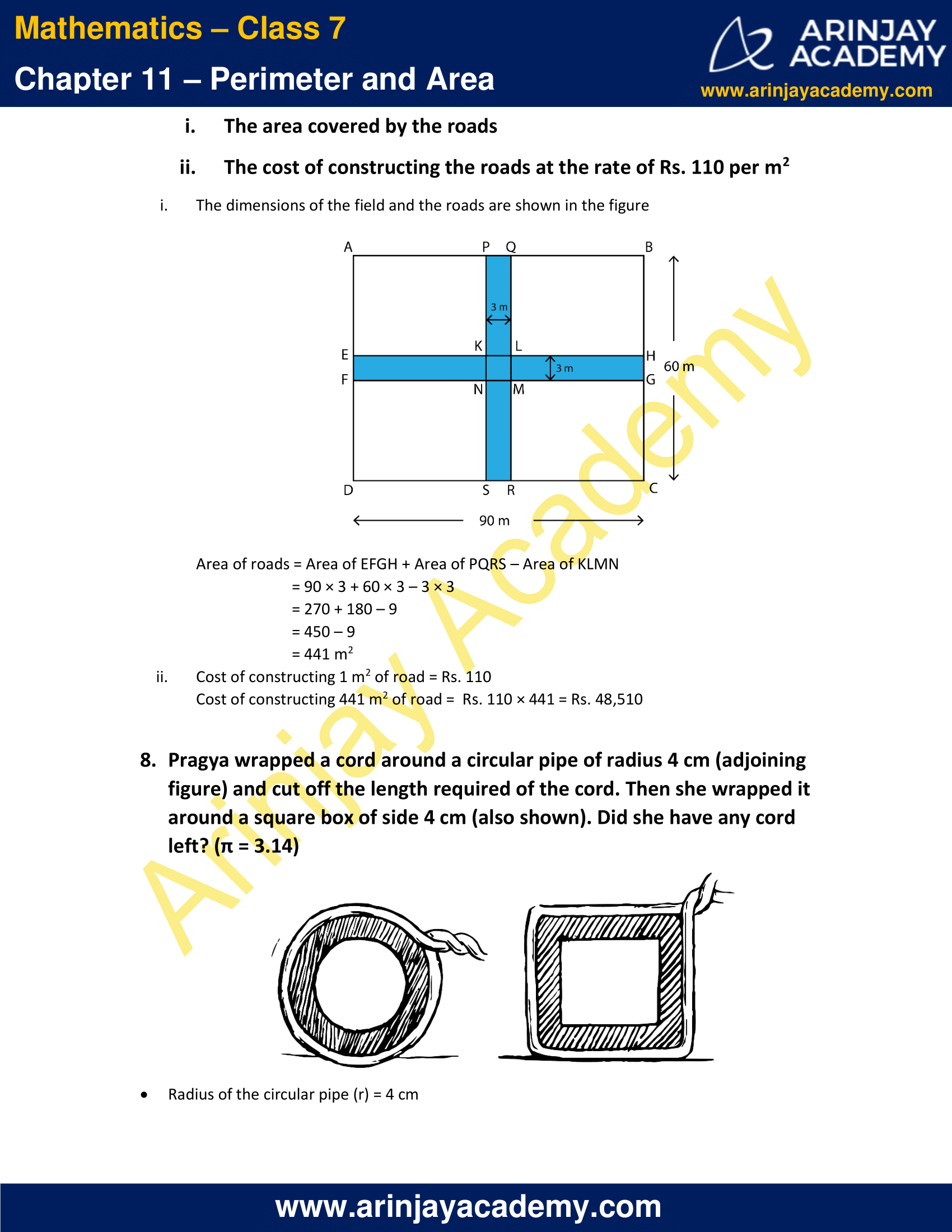
7. Through a rectangular field of length 90 m and breadth 60 m, two roads are constructed which are parallel to the sides and cut each other at right angles through the centre of the fields. If the width of each road is 3 m, find
i. The area covered by the roads
ii. The cost of constructing the roads at the rate of Rs. 110 per m2
Solution:
i. The dimensions of the field and the roads are shown in the figure
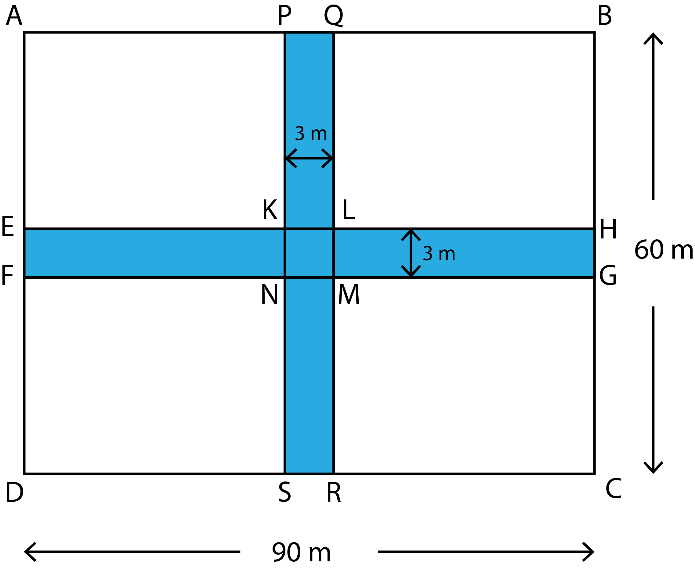
Area of roads = Area of EFGH + Area of PQRS – Area of KLMN
= 90 × 3 + 60 × 3 – 3 × 3
= 270 + 180 – 9
= 450 – 9
= 441 m2
ii. Cost of constructing 1 m2 of road = Rs. 110
Cost of constructing 441 m2 of road = Rs. 110 × 441 = Rs. 48,510
8. Pragya wrapped a cord around a circular pipe of radius 4 cm (adjoining figure) and cut off the length required of the cord. Then she wrapped it around a square box of side 4 cm (also shown). Did she have any cord left? (π = 3.14)
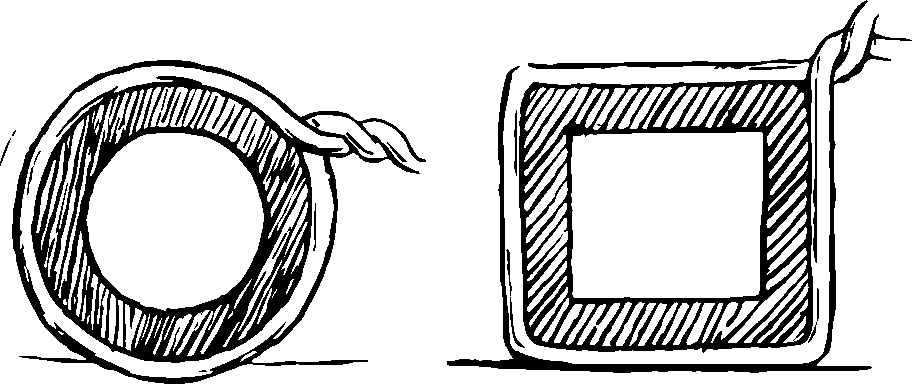
Solution:
Radius of the circular pipe (r) = 4 cm
Side of the square box (s) = 4 cm
Length of cord = Circumference of pipe = 2πr = 2 × 3.14 × 4 = 25.12 cm
Length of cord required to wrap around the square box = Perimeter of the box = 4s = 16 cm
Because the length of cord required to wrap around the box is less than the length of cord Pragya already have, therefore, she will have 9.12 cm (= 25.12 – 16) of cord left.
9. The adjoining figure represents a rectangular lawn with a circular flower bed in the middle. Find:
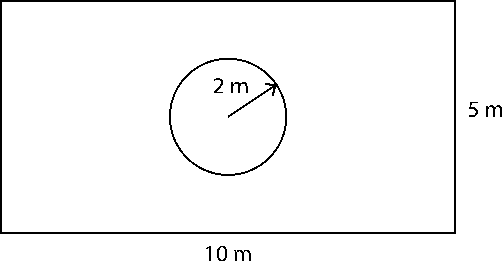
i. The area of whole land
ii. The area of the flower bed
iii. The area of the lawn excluding the area of the flower bed
iv. The circumference of the flower bed
i. Length of lawn = 10 m
Breadth of lawn = 5 m
Area of lawn = Length × Breadth = 10 × 5 = 50 m2
ii. Radius of flower bed (r) = 2 m
Area of flower bed = πr2 = 3.14 × 22 = 12.56 m2
iii. Area of lawn excluding the area of the flower bed = Area of lawn – Area of flower bed
= 50 – 12.56
= 37.44 m2
iv. Circumference of flower bed = 2πr = 2 × 3.14 × 2 = 12.56 m
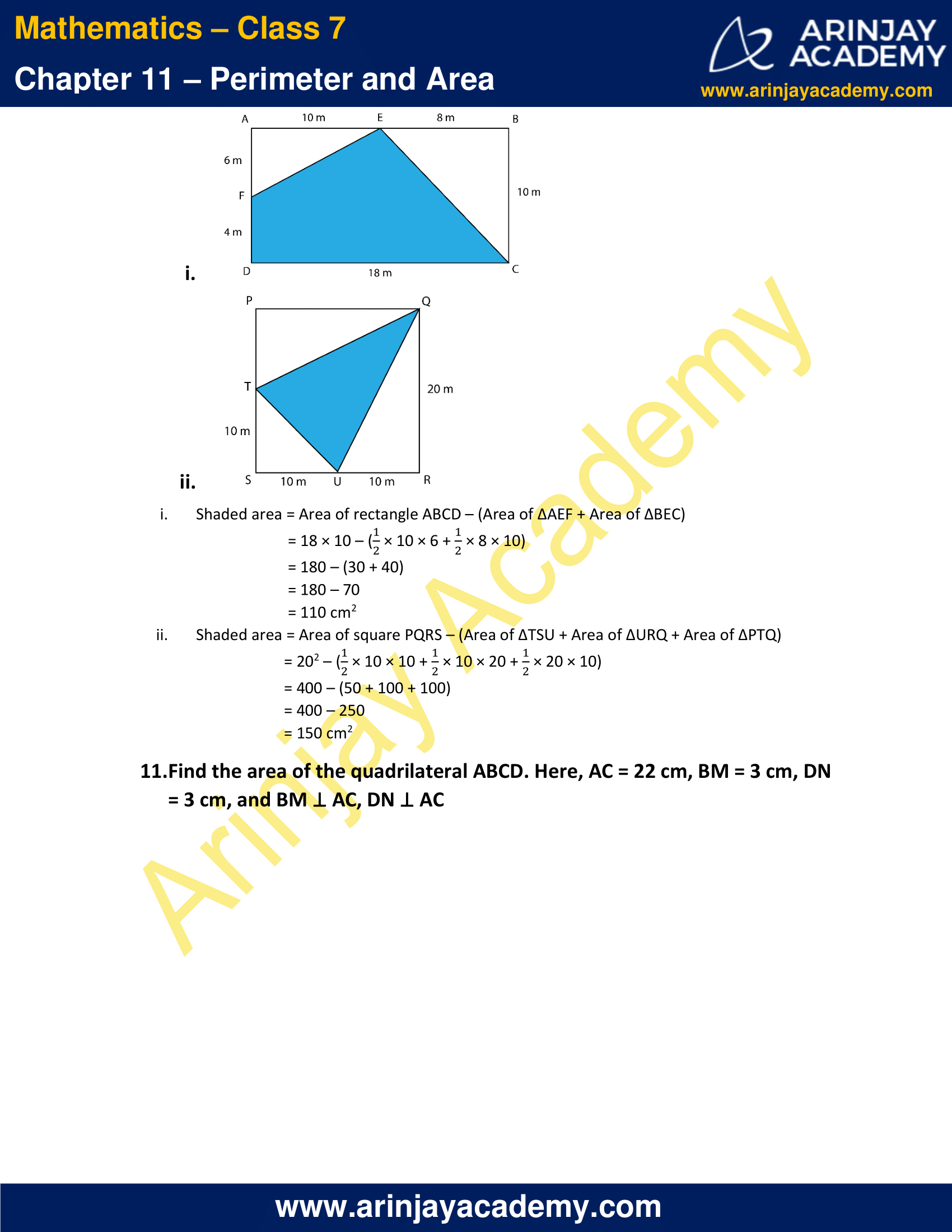
10. In the following figures, find the area of the shaded portions:
i.

ii.

i. Shaded area = Area of rectangle ABCD – (Area of ΔAEF + Area of ΔBEC)
= 18 × 10 – [(1/2) × 10 × 6 + (1/2) × 8 × 10]
= 180 – (30 + 40)
= 180 – 70
= 110 cm2
ii. Shaded area = Area of square PQRS – (Area of ΔTSU + Area of ΔURQ + Area of ΔPTQ)
= 202 – [ (1/2) × 10 × 10 + (1/2) × 10 × 20 + (1/2) × 20 × 10]
= 400 – (50 + 100 + 100)
= 400 – 250
= 150 cm2
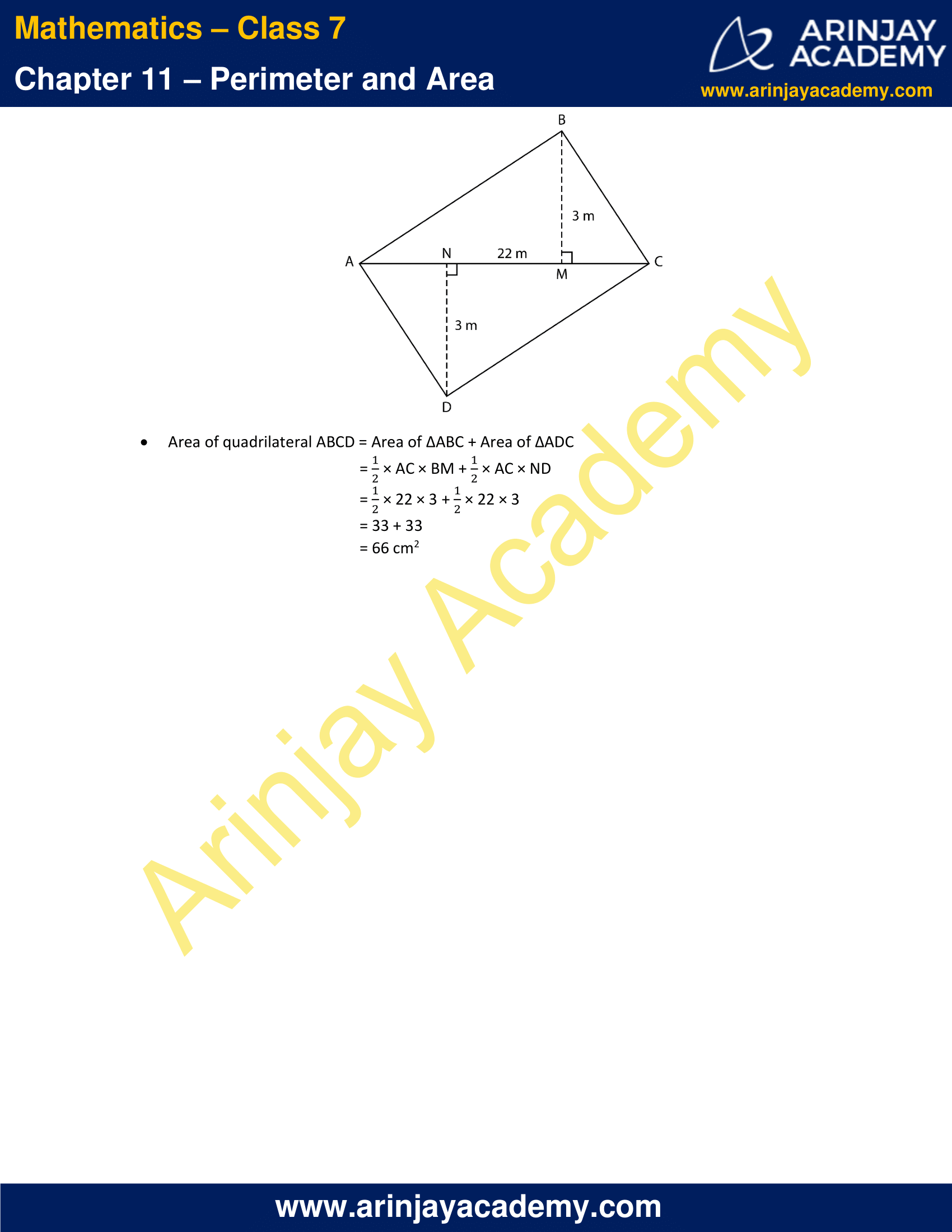
11. Find the area of the quadrilateral ABCD. Here, AC = 22 cm, BM = 3 cm, DN = 3 cm, and BM ⊥ AC, DN ⊥ AC
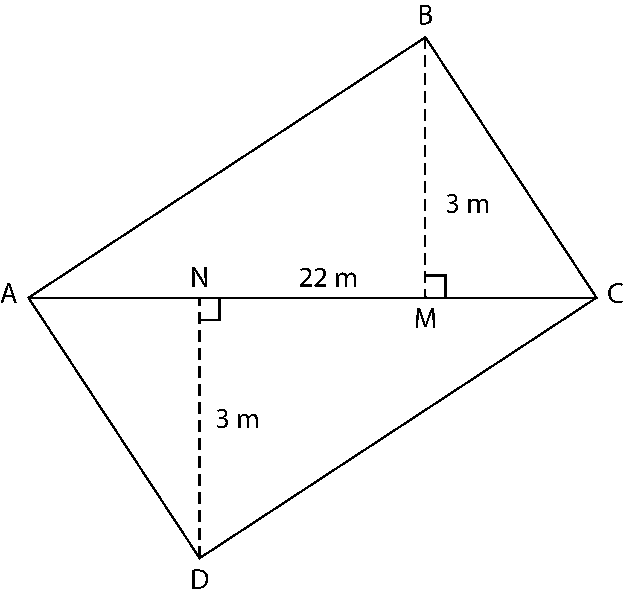
Solution:
Area of quadrilateral ABCD = Area of ΔABC + Area of ΔADC
= (1/2) × AC × BM + (1/2) × AC × ND
= (1/2) × 22 × 3 + (1/2) × 22 × 3
= 33 + 33
= 66 cm2
With this we come to the end of NCERT Solutions for Class 7 Maths Chapter 11 Perimeter and Area. We hope these helped you study your subject.
Download NCERT Solutions for Class 7 Maths Chapter 11 – Perimeter and Area
