NCERT Solutions For Class 10 Maths Chapter 8 Exercise 8.1- Introduction to Trignometry

NCERT Solutions For Class 10 Maths Chapter 8 Exercise 8.1 Introduction to Trigonometry

Solutions For Class 10 Maths Chapter 8 Exercise 8.1 Introduction to Trignometry. The class 10 maths chapter 8 exercise 8.1 contains 5 questions, for which detailed answers have been provided in this note. In case you are looking at studying the remaining Exercise for Class 10 for Maths NCERT solutions for other Chapters, you can click the link at the end of this Note.

Category NCERT Solutions for Class 10
Subject Maths
Chapter Chapter 8
Exercise Exercise 8.1
Chapter Name Introduction to Trignometry

NCERT Solutions For Class 10 Maths Chapter 8 Exercise 8.1- Introduction to Trigonometry

1. In â–³ABC, right-angled at B, AB = 24 cm, BC = 7 cm. Determine:

(i) sin A, cos A
(ii) sin C, cos C

Solution:

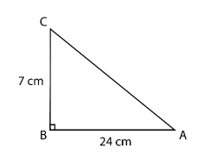
Using the Pythagoras theorem
AC2 = AB2 + BC2
AC2 = 242 + 72
AC2 = 576 + 49
AC2 = 625
AC = \sqrt { 625 } cm = 25 cm

sin A = \cfrac { BC }{ AC } = \cfrac { 7 }{ 25 }
cos A = \cfrac { AB }{ AC } = \cfrac { 24 }{ 25 }    …(i)

sin C = \cfrac { AB }{ AC } = \cfrac { 24 }{ 25 }
cos C = \cfrac { BC }{ AC } = \cfrac { 7 }{ 25 }    …(ii)

 

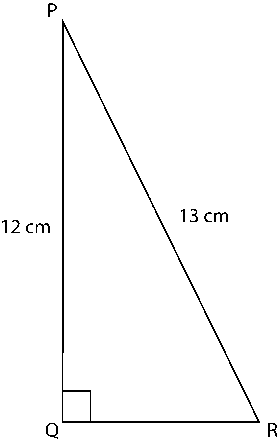
2. In the given figure, find tan(P) – cot(R)

Solution:

In the given triangle
tan(P) = \cfrac { QR }{ PQ }
cot(R) = \cfrac { QR }{ PQ }
tan(P) – cot(R) = \cfrac { QR }{ PQ }  – \cfrac { QR }{ PQ }  = 0




Ex 8.1 Class 10 NCERT Solutions Chapter 8

3. If sin A = \cfrac { 3 }{ 4 } , calculate cos A and tan A.

Solution:

Consider the â–³ABC, right-angled at B such that sin(A) = \cfrac { 3 }{ 4 }

 

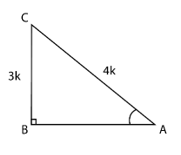
sin(A) = \cfrac { BC }{ AC } = \cfrac { 3 }{ 4 }
∴ BC = 3k, AC = 4k  (k is a positive real number)
Using the Pythagoras theorem
AC2 = AB2 + BC2
(4k)2 = AB2 + (3k)2
AB2 = 16k2 – 9k2
AB2 = 7k2
AB = k√7
cos(A) = \cfrac { AB }{ AC } = \cfrac { k\sqrt { 7 } }{ 4k } = \cfrac { \sqrt { 7 } }{ 4 }
tan(A) = \cfrac { BC }{ AB } = \cfrac { 3k }{ k\sqrt { 7 } }  = \cfrac { 3 }{ \sqrt { 7 } }

 

4. Given 15 cot(A) = 8, find sin(A) and sec(A).

Solution:

Consider the â–³ABC, right-angled at B such that 15 cot(A) = 8

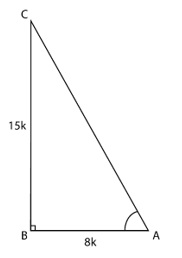
cot(A) = \cfrac { AB }{BC } = \cfrac { 8 }{ 15 }
∴ AB = 8k, BC = 15k  (k is a positive real number)
Using the Pythagoras theorem
AC2 = AB2 + BC2
AC2 = (8k)2 + (15k)2
AC2 = 64k2 + 225k2
AC2 = 289k2
AC = \sqrt { 289{ k }^{ 2 } }  = 17k
sin(A) = \cfrac { BC }{AC } = \cfrac { 15k }{ 17k } = \cfrac { 15 }{ 17 }
sec(A) = \cfrac { AC }{AB } = \cfrac { 17k }{ 8k } = \cfrac { 17 }{8 }

Class 10 Maths Chapter Ex 8.1 Class 10 NCERT Solutions

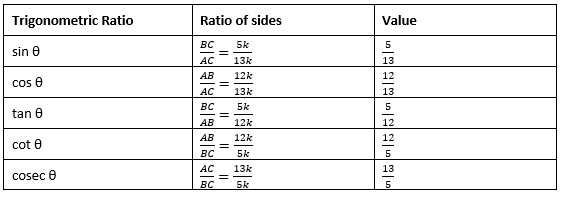
5. Given sec θ = \cfrac { 13 }{12 } , calculate all other trigonometric ratios.

Solution:

Consider the △ABC, right-angled at B such that ∠A = θ

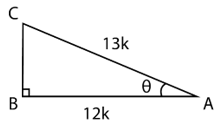
sec θ = \cfrac { AC }{AB } = \cfrac { 13 }{12 }
∴ AB = 12k, AC = 13k       (k is a positive real number)
Using the Pythagoras theorem
AC2 = AB2 + BC2
(13k)2 = (12k)2 + BC2
BC2 = 169k2 – 144k2
BC2 = 25k2
BC = \sqrt { 25{ k }^{ 2 } } = 5k

 

6. If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A and ∠B.

Solution:

Consider two right triangles ACD and BEF, right angled at C and E respectively
Given, cos A = cos B

∴ \cfrac { AC }{AD } = \cfrac { BE }{BF }
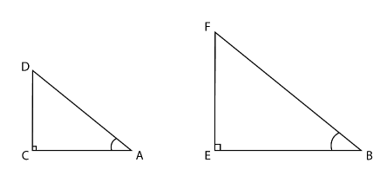
\cfrac { AC }{BE } = \cfrac { AD }{BF } = k   …(i)
Using Pythagoras theorem,
CD = \sqrt { { AD }^{ 2 }-{ AC }^{ 2 } }
= \sqrt { { (k\times BF) }^{ 2 }-{ (k\times BE) }^{ 2 } }
= k\sqrt { { BF }^{ 2 }-{ BE }^{ 2 } }
EF = \sqrt { { BF }^{ 2 }-{ BE }^{ 2 } }
∴ \cfrac { CD }{EF } = \cfrac { k\sqrt { { BF }^{ 2 }-{ BE }^{ 2 } } }{ \sqrt { { BF }^{ 2 }-{ BE }^{ 2 } } } = k     …(ii)
In â–³ACD and â–³BEF
\cfrac { AC }{ BE } = \cfrac { AD }{ BF } = \cfrac { CD }{ EF } = k        (From equation (i) and (ii))
∴ △ACD ~ △BEF   (SSS Similarity Criteria)
⇒ ∠A = ∠B




7. If cot θ = \cfrac { 7 }{ 8 } , evaluate:
i. \cfrac { (1+sin\theta )(1-sin\theta ) }{ (1+cos\theta )(1-cos\theta ) }
ii. cot²θ

Solution:

Consider the △ABC, right-angled at B such that ∠A = θ

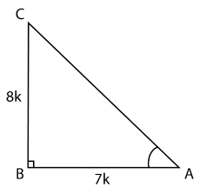
cot θ = \cfrac { AB }{ BC } = \cfrac { 7 }{ 8 }
∴ AB = 7k, BC = 8k  (k is a positive real number)
Using the Pythagoras theorem
AC2 = AB2 + BC2
AC2 = (7k)2 + (8k)2
AC2 = 49k2 + 64k2
AC2 = 113k2
AC = k√113

(i) sin θ = \cfrac { BC }{ AC } = \cfrac { 8k }{ k\sqrt { 113 } } = \cfrac { 8 }{ \sqrt { 113 } }

cos θ = \cfrac { AB }{ AC } = \cfrac { 7k }{ k\sqrt { 113 } } = \cfrac { 7 }{ \sqrt { 113 } }

\cfrac { (1+sin\theta )(1-sin\theta ) }{ (1+cos\theta )(1-cos\theta ) }
= \cfrac { (1-{ sin }^{ 2 }\theta ) }{ (1-{ cos }^{ 2 }\theta ) }
= \cfrac { 1-{ \left( \cfrac { 8 }{ \sqrt { 113 } } \right) }^{ 2 } }{ 1-{ \left( \cfrac { 7 }{ \sqrt { 113 } } \right) }^{ 2 } }
= \cfrac { 1-\cfrac { 64 }{ 113 } }{ 1-\cfrac { 49 }{ 113 } }
= \cfrac { \cfrac { 113-64 }{ 113 } }{ \cfrac { 113-49 }{ 113 } }
= \cfrac { 113-64 }{ 113-49 }
= \cfrac { 49 }{ 64 }

(ii) cot2θ = { \left( \cfrac { 7 }{ 8 } \right) }^{ 2 } = \cfrac { 49 }{ 64 }

Class 10 Maths Ex 8.1 NCERT Solutions

8. If 3 cot A = 4, check whether \cfrac { (1-{ tan }^{ 2 }A) }{ (1+{ tan }^{ 2 }A) } = cos2A – sin2A or not.

Solution:

Consider the â–³ABC, right-angled at B

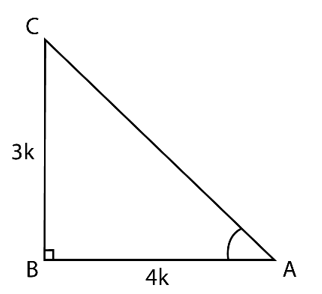
cot A = \cfrac { AB }{ BC } = \cfrac { 4 }{ 3 }
∴ AB = 4k, BC = 3k  (k is a positive real number)
Using the Pythagoras theorem
AC2 = AB2 + BC2
AC2 = (4k)2 + (3k)2
AC2 = 16k2 + 9k2
AC2 = 25k2
AC = 5k
sin A = \cfrac { BC }{ AC } = \cfrac { 3k }{ 5k } = \cfrac { 3 }{ 5 }
cos A = \cfrac { AB }{ AC } = \cfrac { 4k }{ 5k } = \cfrac { 4 }{ 5 }
tan A = \cfrac { BC }{ AB } = \cfrac { 3k }{ 4k } = \cfrac { 3 }{ 4 }
LHS = \cfrac { (1-{ tan }^{ 2 }A) }{ (1+{ tan }^{ 2 }A) }
=\cfrac { 1-{ \left( \cfrac { 3 }{ 4 } \right) }^{ 2 } }{ 1+{ \left( \cfrac { 3 }{ 4 } \right) }^{ 2 } }
= \cfrac { 1-\cfrac { 9 }{ 16 } }{ 1+\cfrac { 9 }{ 16 } }
=\cfrac { { \left( \cfrac { 16-9 }{ 16 } \right) } }{ { \left( \cfrac { 16+9 }{ 16 } \right) } }
=\cfrac { 16-9 }{ 16+9 }
=\cfrac { 7 }{ 25 }
RHS = cos2A – sin2A
={ \left( \cfrac { 4 }{ 5 } \right) }^{ 2 } – { \left( \cfrac { 3 }{ 5 } \right) }^{ 2 }
=\cfrac { 16 }{ 25 } – \cfrac { 9 }{ 25 }
=\cfrac { 7 }{ 25 }
Hence, \cfrac { (1-{ tan }^{ 2 }A) }{ (1+{ tan }^{ 2 }A) } = cos2A – sin2A

 

9. In a triangle ABC, right angled at B, if tan A = \cfrac { 1 }{ \sqrt { 3 } } , find the value of:
i. sin A cos C + cos A sin C
ii. cos A cos C – sin A sin C

Solution:

In â–³ABC

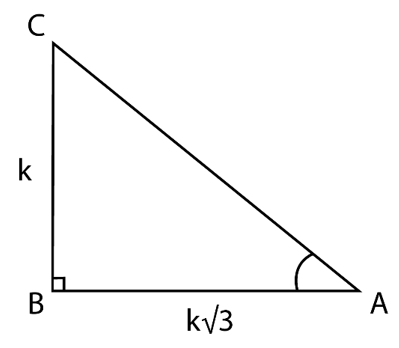
tan A = \cfrac { BC }{ AB } = \cfrac { 1 }{ \sqrt { 3 } }
∴ AB = k√3 , BC = k     (k is a positive real number)
Using the Pythagoras theorem
AC2 = AB2 + BC2
AC2 = (k√3 )2 + (k)2
AC2 = 3k2 + k2
AC2 = 4k2
AC = 2k

sin A = \cfrac { BC }{ AC } = \cfrac { k }{ 2k } = \cfrac { 1 }{ 2 }
cos A = \cfrac { AB }{ AC } = \cfrac { k\sqrt { 3 } }{ 2k } = \cfrac { \sqrt { 3 } }{ 2 }

sin C = \cfrac { AB }{ AC } = \cfrac { k\sqrt { 3 } }{ 2k } = \cfrac { \sqrt { 3 } }{ 2 }
cos C = \cfrac { BC }{ AC } = \cfrac { k }{ 2k } = \cfrac { 1 }{ 2 }

(i) sin A cos C + cos A sin C
= \cfrac { 1 }{ 2 } \times \cfrac { 1 }{ 2 } +\cfrac { \sqrt { 3 } }{ 2 } \times \cfrac { \sqrt { 3 } }{ 2 }
= \cfrac { 1 }{ 4 } \times \cfrac { 3 }{ 4 }
= \cfrac { 4 }{ 4 }
= 1

(ii) cos A cos C – sin A sin C
= \cfrac { \sqrt { 3 } }{ 2 } \times \cfrac { 1 }{ 2 } -\cfrac { 1 }{ 2 } \times \cfrac { \sqrt { 3 } }{ 2 }
= \cfrac { \sqrt { 3 } }{ 4 } -\cfrac { \sqrt { 3 } }{ 4 }
= 0

 

10. In â–³PQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P, and tan P.

Solution:

Let PR = x
∵ PR + QR = 25
∴ QR = 25 – x

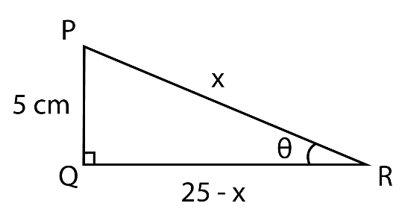
Using Pythagoras Theorem
PR2 = PQ2 + QR2
x2 = 52 + (25 – x)2
x2 = 25 + 252 + x2 – 50x
50x = 25 + 625
50x = 650
x = 13

PR = x = 13 cm
QR = 25 – x = 25 – 13 = 12 cm

sin P = \cfrac { QR }{ PR } = \cfrac { 12 }{ 13 }
cos P = \cfrac { PQ }{ PR } = \cfrac { 5 }{ 13 }
tan P = \cfrac { QR }{ PQ } = \cfrac { 12 }{ 5 }




11. State whether the following are true or false. Justify your answer.

1. The value of tan A is always less than 1

False
tan A = \cfrac { side\quad opposite\quad to\quad A }{ side\quad adjacent\quad to\quad A }
If the side opposite to A is greater than the side adjacent to A, then tan A is greater than 1.

ii. sec A = \cfrac { 12 }{ 5 } for some value of angle A.

True
sec A = \cfrac { hypotenuse }{ side\quad adjacent\quad to\quad A } = \cfrac { 12 }{ 5 }
Hypotenuse is greater than the other side, therefore it is possible for some value of A.

iii. cos A is the abbreviation used for the cosecant of angle A

False
cos A means cosine of angle A
cosecant of A is represented by cosec A

iv. cot A is the product of cot and A

False
‘cot’ is a function. cot A means cotangent of A. It is not the product of cot and A.

v. sin θ = \cfrac { 4 }{ 3 } for some angle θ

False
sin θ = \cfrac { side\quad opposite\quad to\quad A }{ hypotenuse }  = \cfrac { 4 }{ 3 }
In this case, the hypotenuse is shorter and the side opposite to the angle A is larger which is not possible.

NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.1 – Introduction to Trignometry, has been designed by the NCERT to test the knowledge of the student on the topic – Trigonometric Ratios

Download NCERT Solutions For Class 10 Maths Chapter 8 Exercise 8.1 – Introduction to Trigonometry

NCERT Solutions for Class 10

CBSE Notes for Class 10

MCQ Questions for Class 10

Leave a Comment