NCERT Solutions For Class 10 Maths Chapter 4 Exercise 4.4 Quadratic Equations

NCERT Solutions For Class 10 Maths Chapter 4 Ex. 4.4 Quadratic Equations

Download NCERT Solutions For Class 10 Maths Chapter 4 Exercise 4.4 Quadratic Equations. This Exercise contains 5 questions, for which detailed answers have been provided in this note. Quadratic Equations exercise 4.4 class 10 chapter 4 NCERT Solutions have been explained in a simple and easy-to-understand language to help you learn and prepare for your upcoming class 10 Maths exams. Here we are sharing Quadratic Equations ex 4.4 class 10 solution.

Category NCERT Solutions for Class 10
Subject Maths
Chapter Chapter 4
Exercise Exercise 4.4
Chapter Name Quadratic Equations

NCERT Solutions For Exercise 4.4 class 10 Maths Chapter 4 Quadratic Equations

You can also download the free PDF of NCERT Solutions Chapter 4 Ex 4.4 Quadratic Equations for your online exam preparation.




Quadratic Equations NCERT Solutions For Class 10 Maths Chapter 4 Exercise 4.4

1. Find the nature of the roots of the following quadratic equation. If the real roots exist, find them:

Solution: We know that the quadratic equation ax2+bx+c = 0 has

(a) Two distinct real roots, if b2-4ac > 0,
(b) Two equal real roots, if b2-4ac = 0,
(c) No real roots, if b2-4ac < 0.

(i) 2x2-3x+5 = 0

Solution: Comparing the given quadratic equation with the general form of quadratic equation ax2+bx+c = 0 we get

a = 2, b = -3 and c = 5

Then, b2-4ac = (-3)2-4×2×5 = 9-40 = -31 < 0

Hence the given quadratic equation has no real roots.

(ii) 3x2-4√3x+4 = 0

Solution: Comparing the given quadratic equation with the general form of quadratic equation ax2+bx+c = 0 we get

a = 3, b = -4√3 and c = 4

Then, b2-4ac = (-4√3)2-4×3×4 = 48-48 = 0

Hence the given quadratic equation has two equal real roots.

And the roots of the equation are given by

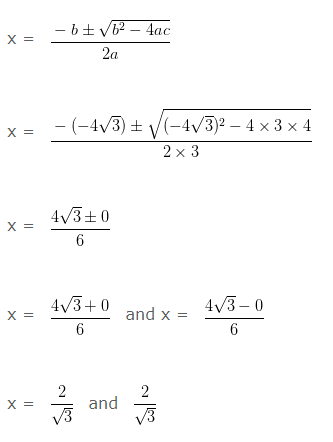
(iii) 2x2-6x+3 = 0

Solution: Comparing the given quadratic equation with the general form of quadratic equation ax2+bx+c = 0 we get

a = 2, b = -6 and c = 3

then, b2-4ac = (-6)2-4×2×3 = 36-24 = 12 > 0

Hence the given quadratic equation has two distinct real roots.

And the roots of the equation are given by




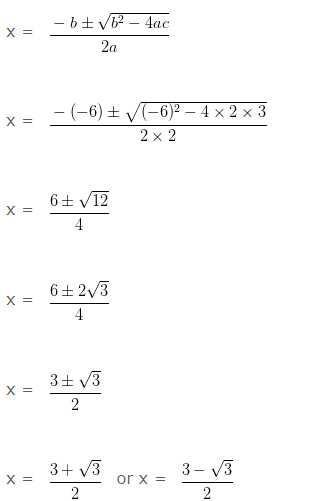
Ex 4.4 Class 10 Maths Question 2 Solution 

2. Find the value of k for each of the following quadratic equations, so that they have two equal roots.

(i) 2x2+kx+3 = 0

Solution: Comparing the given quadratic equation with the general form of quadratic equation ax2+bx+c = 0 we get

a = 2, b = k and c = 3

Now the given quadratic equation have two equal roots if

b2-4ac = 0

(k)2-4×2×3 = 0

k2-24 = 0

k2 = 24

k = ±√24

k = ± 2√6

Therefore, the required value of k is ± 2√6.

(ii)  kx(x-2)+6 = 0

Solution: The given quadratic equation can be written as

kx2-2kx+6 = 0….(1)

Comparing the quadratic equation (1) with the general form of quadratic equation ax2+bx+c = 0 we get

a = k, b = -2k and c = 6

Now the given quadratic equation have two equal roots if

b2-4ac = 0

(-2k)2-4×k×6 = 0

4k2-24k = 0

4k(k-6) = 0

k(k-6) = 0

k = 0

Or, k-6 = 0

k = 6

If k = 0, then equation will not have x2 and x, which is not possible because the given equation is quadratic equation.

Therefore, the required value of k is 6.

NCERT Solutions For Exercise 4.4 Class 10 Maths Chapter 4

3. Is it possible to design a rectangular mango grove whose length is twice its breadth and the area is 800 m2. If so find its length and breadth.

Solution: Let the breadth of the mango grove be x m and the length is 2x m.

Area = length × breadth

= x × 2x

= 2x2 m2

Then by the given condition,

2x2 = 800

x2 = 400

x = ±√400

x = ±20

Since, length cannot be negative, then x ≠ -20

Hence it is possible to design a rectangular mango grove whose length is twice its breadth and the area is 800 m2 and its breadth is 20 m and length is 20×2 = 40 m

 

4. Is the following situation possible? If so, determine their present ages

The sum of the ages of two friends is 20 years. Four years ago, the product of their ages in years was 48.

Solution: Let the age of 1st friend is x.

Then the age of 2nd friend is (20-x)

Four year ago their age was (x-4) and (20-x-4)

Then using the given condition we have

(x-4)(16-x) = 48

16x – 64 – x2 +4x = 48

20x – x2 – 64 – 48 = 0

x2 – 20x + 112 = 0……(1)

Now comparing the above quadratic equation with the general form of quadratic equation ax2+bx+c = 0 we get

a = 1, b = -20 and c = 112

then, b2-4ac = (-20)2-4×1×112 = 400-448 = -48 > 0

Therefore, no real root is possible for this equation and hence this situation is not possible.




5. Is it possible to design a rectangular park of perimeter 80 m and area 400 m2? If so find its length and breadth.

Solution: Let the length and breadth of the park be “l” and “b”

Area of rectangle = 2(l + b)

2(l + b) = 80

l + b = 40

b = 40 – l

Then, Area = l(40 – l)

Then by the given condition,

l(40 – l) = 400

40l  – l2 -400 = 0

l2 – 40l + 400 = 0….(1)

Now comparing the above quadratic equation with the general form of quadratic equation ax2+bx+c = 0 we get

a = 1, b = -40 and c = 400

Then, b2-4ac = (-40)2-4×1×400 = 1600-1600 = 0

As the quadratic equation has two equal roots then the given situation is possible.

And the solution of the equation (1) is given by

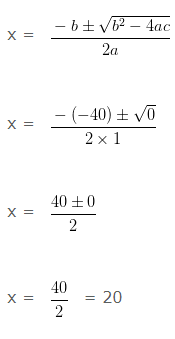
Therefore, the length of the park is 20 m, and the breadth of the park = 40 – l =  40-20 = 20 m.

NCERT Solutions for Class 10 Maths Chapter 4 Exercise 4.4 Quadratic Equations, has been designed by the NCERT to test the knowledge of the student on the topic Nature of Roots.

NCERT Solutions for Class 10 Maths

Download NCERT Solutions For ex 4.4 class 10 Maths chapter 4 Quadratic Equations

NCERT Solutions for Class 10

CBSE Notes for Class 10

MCQ Questions for Class 10

Leave a Comment