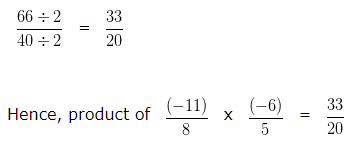Multiplication of Rational Numbers

Multiplication of Rational Numbers Examples
Example 1
Find the product of 15/7 and 3/5?
Explanation

To further simplify the given numbers into their lowest form, we would divide both the Numerator and Denominator by their HCF
HCF of 45 and 35 is 5
Dividing both the Numerator and Denominator by their HCF
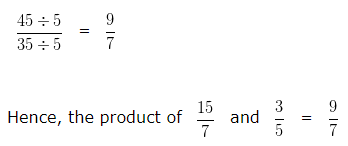
Multiplication of Rational Numbers – Example 2
Find the product of 9/7 and -12/8?
Explanation

To further simplify the given numbers into their lowest form, we would divide both the Numerator and Denominator by their HCF
HCF of 108 and 56 is 4
Dividing both the Numerator and Denominator by their HCF
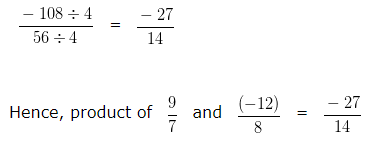
Multiplication of Rational Numbers – Example 3
Find the product of -4/7 and 8/12?
Explanation

To further simplify the given numbers into their lowest form, we would divide both the Numerator and Denominator by their HCF
HCF of 32 and 84 is 4
Dividing both the Numerator and Denominator by their HCF
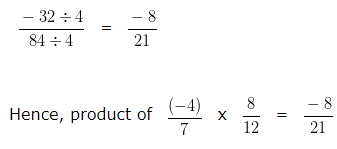
Multiplication of Rational Numbers – Example 4
Find the product of -11/8 x -6/5?
Explanation
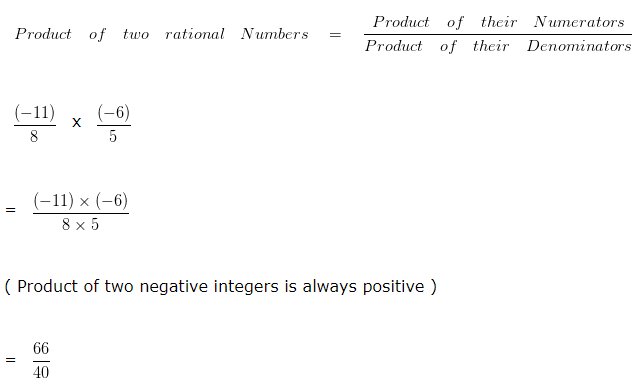
To further simplify the given numbers into their lowest form, we would divide both the Numerator and Denominator by their HCF
HCF of 66 and 40 is 2
Dividing both the Numerator and Denominator by their HCF