Multiplication For Class 4

Multiplication For Class 4, deals with various concepts which are as under:-

• Properties of Multiplication
• Multiplication with Multiplier ending with zeros
• Multiplication of 4 digit number with 1 digit number
• Multiplying 3 digit Numbers by 2 Digit Numbers
• Multiplying 4 digit Number with 2 Digit Numbers
• Multiplying 3 digit Numbers by 3 Digit Numbers

Multiplication For Class 4 – Properties of Multiplication

Question 1

Which of the following equations shows the Commutative Property of Multiplication?

a) 4 x 3 = 3 x 4

b) ( 4 x 3 ) x 5 = 4 x ( 3 x 5 )

c) 4 x 1 = 4

Explanation:

According to the Commutative Property of Multiplication, if we change the order of Multiplicand and Multiplier, the product remains the same i.e,

a x b = b x a

Hence, 4 x 3 = 3 x 4 satisfies Commutative Property of Multiplication.

Question 2

Which of the following equations shows the Associative Property of Multiplication?

a) 14 x 6 = 6 x 14

b) 6 x 1 = 6

c) ( 14 x 6 ) x 18 = 14 x ( 6 x 18 )

Explanation:

According to the Associative Property of Multiplication, if we multiply more than two numbers, they can be grouped but the product remains the same i.e,

(a x b) x c = a x (b x c)

Hence, ( 14 x 6 ) x 18 = 14 x ( 6 x 18 ) satisfies Associative Property of Multiplication.

Question 3

Which of the following equations shows the Property of Multiplicative Identity?

a) 9 x 1 = 9

b) ( 12 x 15 ) x 9 = 12 x ( 15 x 9 )

c) 12 x 15 = 15 x 12

Explanation:

According to the Property of Multiplicative Identity, if we multiply any number with 1, then the product is the number itself.

a x 1 = a

Hence, 9 x 1 = 9 satisfies Property of Multiplicative Identity.

 

Multiplication For Class 4 – Multiplication with Multiplier ending with zeros

Question 4

Find the product :

7 x 20 = ?

Explanation:

To Multiply a given number with a Multiplier having zero at the end, we first count the number of zeros.

In 20 there is 1 zero

Now we would multiply, the remaining digits of the given numbers, excluding zeros

i.e

Multiplying 7 by 2

7 x 2 = 14

Add 1 zero after the product 14

The number would be 140

Hence

7 x 20 = 140

Question 5

Find the product :

14 x 200 = ?

Explanation:

To Multiply a given number with a Multiplier having zero at the end, we first count the number of zeros.

In 200 there are 2 zeros

Now we would multiply, the remaining digits of the given numbers, excluding zeros

i.e

Multiplying 14 by 2

14 x 2 = 28

Add 2 zeros after the product 28

The number would be 2800

Hence

14 x 200 = 2800

 

Multiplication For Class 4 – Multiplication of 4 digit number with 1 digit number

Question 6

Find the product.
4253 x 4 = ?

Explanation:

Step I: Multiply 3 in ones place with 4
3 x 4 = 12
Since, the number is more than 9, we need to carry over 1 to the tens place.
Write 2 in ones place.

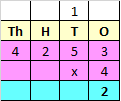
Step II: Multiply 5 in tens place with 4
5 x 4 = 20
Add the carry over of 1 to 20
20 + 1 = 21
Since, the number is more than 9, we need to carry over 2 to the hundreds place.
Write 1 in tens place.

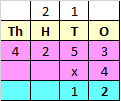
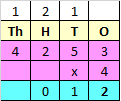
Step III: Multiply 2 in hundreds place with 4
2 x 4 = 8
Add the carry over of 2 to 8
8 + 2 = 10
Since, the number is more than 9, we need to carry over 1 to the thousands place.
Write 0 in hundreds place.

Step IV: Multiply 4 in thousands place with 4
4 x 4 = 16
Add the carry over of 1 to 16
16 + 1 = 17
Since, the number is more than 9, we need to carry over 1 to the ten thousands place.
Write 1 in ten thousands place and 7 in thousands place.

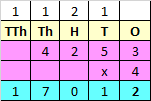
Hence, 4253 x 4 = 17012

Multiplication For Class 4 – Multiplying 3 digit Numbers by 2 Digit Numbers

Question 7

Find the product.
548 x 36

Explanation:

Whenever we multiply a three digit Multiplicand with two digit Multiplier, we first multiply the Multiplicand with ones place of Multiplier, and then multiply Multiplicand with Tens place of the Multiplier.
Step I : Multiply Multiplicand with ones place of Multiplier.
i.e, 548 x 6 = 3288​

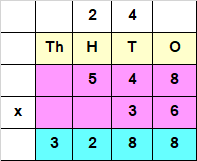
Step II : Multiply Multiplicand with tens place of Multiplier.
i.e, 548 x 3 = 1644

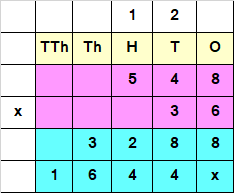
Since the Number obtained at Step II, has a Tens value, we add a “0” or “x” at the end of the answer obtained by multiplying Multiplicand with Tens place of the Multiplier.
Step III : Add both the numbers

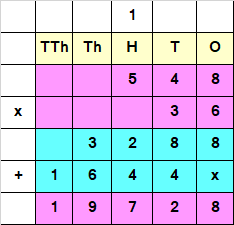
Hence, 548 x 36 = 19728

 

Multiplication For Class 4 – Multiplying 4 digit Number with 2 Digit Numbers

Question 8

Find the product.
6524 x 34

Explanation:

Whenever we multiply a Four digit Multiplicand with two digit Multiplier, we first multiply the Multiplicand with ones place of Multiplier, and then multiply Multiplicand with Tens place of the Multiplier.
Step I : Multiply Multiplicand with ones place of Multiplier.
i.e, 6524 x 4 = 26096

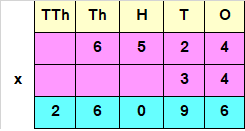
Step II : Multiply Multiplicand with tens place of Multiplier.
i.e, 6524 x 3 = 19572

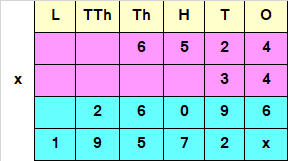
Since the Number obtained at Step II, has a Tens value, we add a 0 or X at the end of the answer obtained by multiplying Multiplicand with Tens place of the Multiplier.
Step III : Add both the numbers

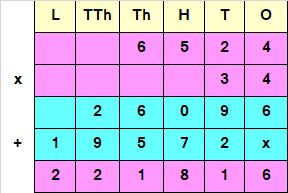
Hence, 6524 x 34 = 221816

Multiplication For Class 4 – Multiplying 3 digit Numbers by 3 Digit Numbers

Question 9

Find the product.
453x 528

Explanation:

Whenever we multiply a three digit Multiplicand by three digit Multiplier, we first multiply the Multiplicand with ones place of Multiplier, then with Tens place of the Multiplier and lastly by Hundreds place.
Step I : Multiply Multiplicand with ones place of Multiplier.
i.e, 453 x 8 = 3624​

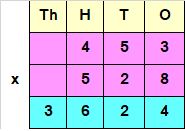
Step II : Multiply Multiplicand with tens place of Multiplier.
i.e, 453 x 2 = 906

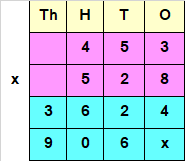
Since the Number obtained at Step II, has a Tens value, we add a “0” or “X” at the end of the answer obtained by multiplying Multiplicand with Tens place of the Multiplier.
Step III : Multiply Multiplicand with hundreds place of Multiplier.
i.e, 453 x 5 = 2265

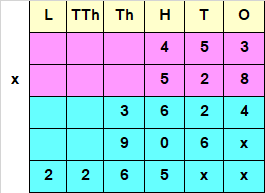
Since the Number obtained at Step III, has a Hundreds place value, we add two “0” or “x” at the end of the answer obtained by multiplying Multiplicand with Hundreds place of the Multiplier.
Step IV : Add all the numbers

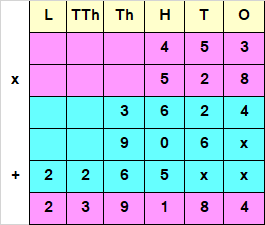
Hence, 453 x 528 = 239184

Click here for Class 4 Chapterwise Explanations